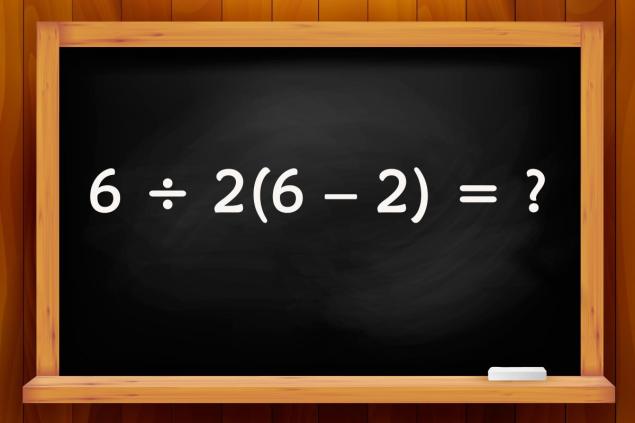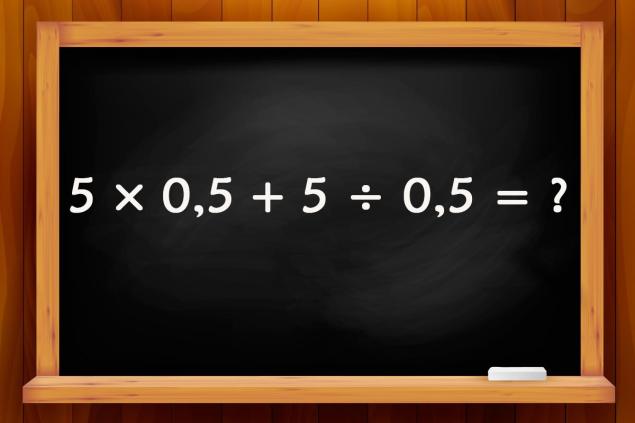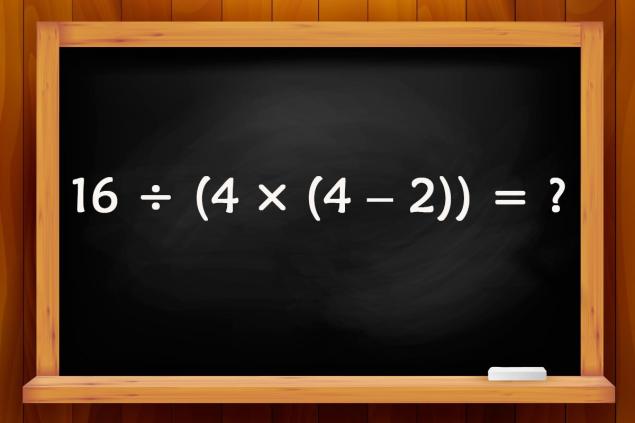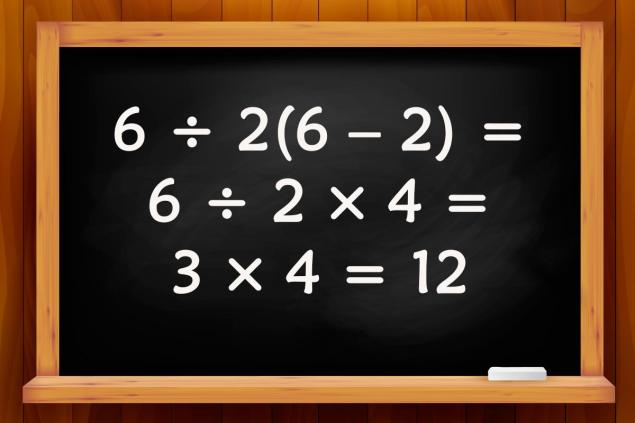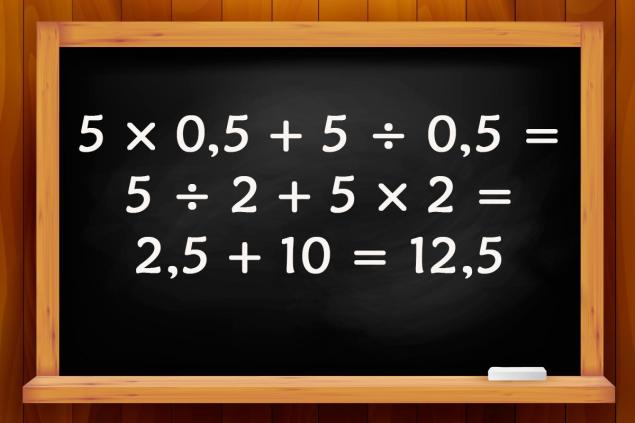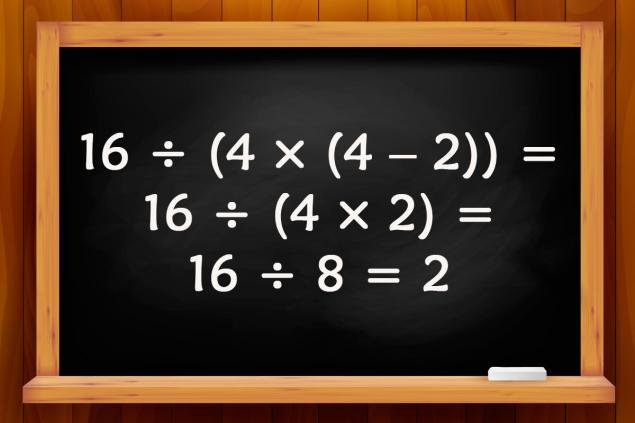Los estudiantes de la escuela soviética resuelven el ejemplo en 1 minuto

Hemos hablado repetidamente sobre la importancia de dar al cerebro una variedad de cargas. Después de todo, la rutina cotidiana claramente no afecta incluso a la persona más inteligente de una manera positiva.

Y resolver varios problemas, rompecabezas y ejemplos ayuda a mantenerse en buena forma. Y siempre lo sabrás, Cómo explicar las matemáticas a un niñoSi esta ciencia importante por alguna razón no se le dará.

Así que la oficina editorial de hoy. "Site" Ofrece algunos ejemplos más interesantes. Tal vez para los excelentes estudiantes redondos no hay nada archicomplex. Sin embargo, también pueden cometer un error. Y no hay nada que decir sobre los C-listas de ayer - será una prueba difícil para ellos.



Cómo explicar las matemáticas a un niño

1. El primer ejemplo no parece desalentador. Pero esta es una impresión engañosa, porque a menudo se cometen errores aquí. Trate de ver todos los obstáculos para dar una respuesta inequívoca y correcta.
   
   
   
   
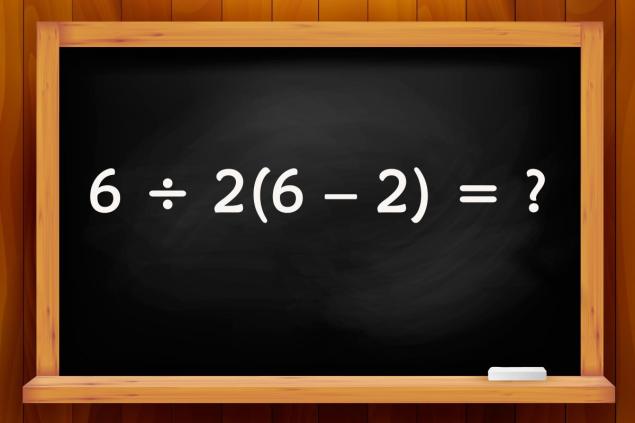
2. En la segunda tarea no hay corchetes, pero aquí tendrá que tratar con fracciones decimales. Y si la multiplicación de la mayoría de los lectores son capaces de dominar, entonces ¿qué hay de dividir por fracción? ¿Recuerdas las reglas matemáticas necesarias? Intenta recordar poner un ejemplo.
   
   
   
   
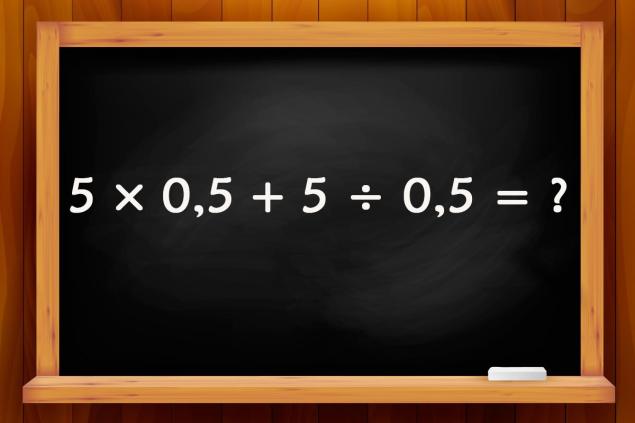
3. Los soportes dobles pueden confundir a muchos. Y como necesitan ser divulgados de todos modos, esto puede ser un problema serio. ¿Puedes conseguir dar la respuesta correcta?
   
   
   
   

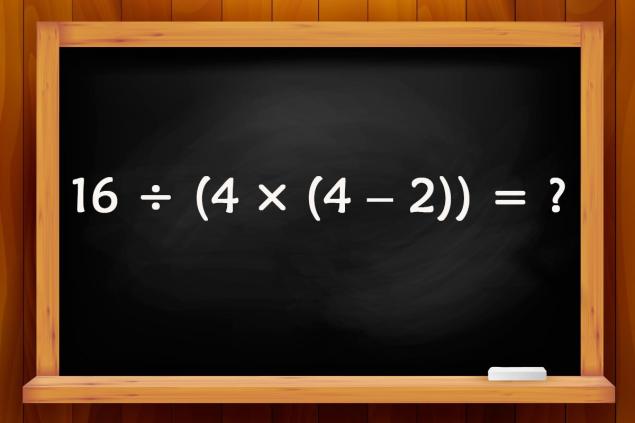
Consejos y soluciones

1. Aquí primero realizamos acciones aritméticas entre corchetes, y luego nos movemos de izquierda a derecha. Entonces 6 ÷ 2(6 – 2) = 6 ÷ 2 × 4 = 3 × 4 = 12.
   
   
   
   
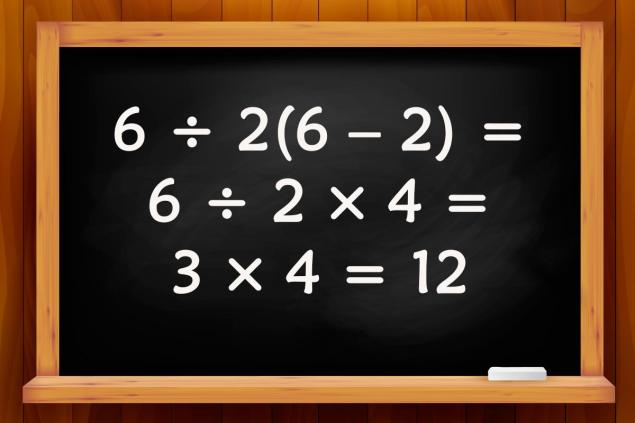
2. Multiplicar por 0,5 es como dividir por 2. Dividir por 0,5 es como multiplicar por 2. Así que tenemos 5 × 0,5 + 5 ÷ 0,5 = 5 ÷ 2 + 5 × 2 = 2,5 + 10 = 12,5
   
   
   
   
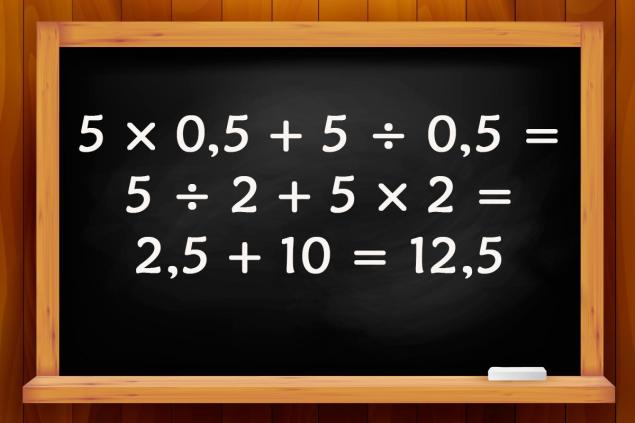
3. El último ejemplo es similar al primero, pero los dobles corchetes dan vuelta a la situación. Después de todo, primero tendrá que realizar todas las operaciones aritméticas en dobles corchetes, y sólo entonces dividir. Por lo tanto, 16 ÷ (4 × (4 - 2)) = 16 ÷ (4 × 2) = 16 ÷ 8 = 2.
   
   
   
   

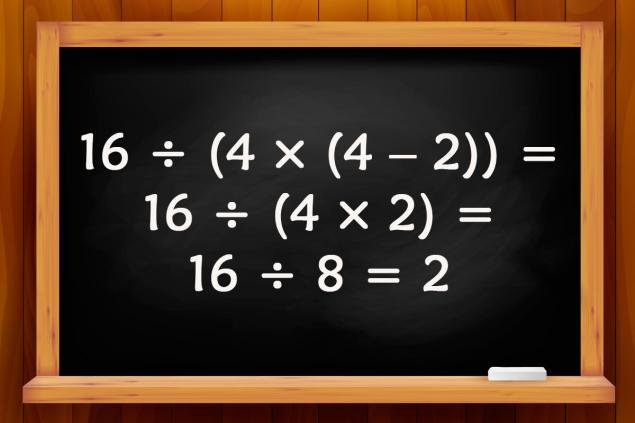
Comparte tus respuestas en los comentarios. Y también resolver nuestros ejemplos más complejos para consolidar el éxito. O tratar de resolver los difíciles puzzles que publicamos el otro día.