The paradox of the wheel over which Aristotle and Galileo puzzled

The wheel paradox was first discussed before Aristotle, but he was the first to study it. Then Galileo Galilei struggled to solve this problem.

The essence of the paradox is as follows:

We have two wheels of different sizes located one in the other. Both wheels roll synchronously and travel a certain distance. The question is, will both wheels go the same way?



If you look closely at the GIF at the top, you will notice that both wheels completely rotate around their circumference to cover the same distance (see the red line). It is also obvious that one circle is smaller than the other. This means that either the wheels have the same circle (which is fundamentally wrong), or different circles “turn” to the same length (which can not be).

What if we pretend it's all true? Then it is technically possible that a wheel with a circumference of 2.54 centimeters can go the same way in one revolution as a wheel with a circumference of 1.6 kilometers.

But that just doesn't happen. A circle with a smaller radius cannot be equal to a circle with a larger radius. So what is it?

Let's trace the path that each point of the circle travels from the beginning of the red line to the end. Move your finger along the line indicating the radius of the circle, while monitoring the trajectory that the small circle travels from the beginning to the end.

Then trace the trajectory that a large circle travels from the beginning to the end. Obviously, a point on a larger circle takes a longer trajectory, and therefore a longer path, to get to the same point.

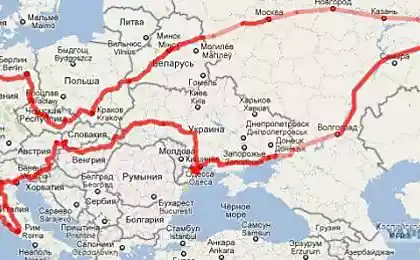
In other words, you can go to Moscow from Nizhny Novgorod through Vladimir, or through Arkhangelsk or Astrakhan. The distance from Nizhny to Moscow remains unchanged, but the paths that will have to be made along these routes are far from the same.

This is the explanation of the paradox over which the most outstanding minds of mankind have puzzled.

source

Source: /users/147