亚里士多德和伽利略拼凑的轮子的悖论

车轮悖论最早在亚里士多德之前被讨论过,但他最早研究过. 后来伽利略·加利莱为解决这个问题而挣扎.

悖论的实质如下:

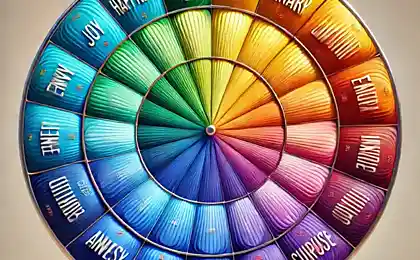
我们有两个不同大小的轮子 位于另一个。 两种轮子都同步滚动并行走一定距离. 问题是,两个车轮都一样吗?



如果仔细查看顶部的GIF,你会注意到两个轮子完全围绕其环绕来旋转来覆盖相同的距离(参见红线). 同样明显的是,一个圆圈比另一个圆圈还小. 这意味着轮子要么有相同的圆(根本错误),要么有不同的圆"转"到相同的长度(不可能).

如果我们假装一切都是真的呢? 然后从技术上讲,一个圆周2.54公分的轮子在一次革命中可以和圆周1.6公里的轮子一样走.

但是这不会发生。 半径较小的圆不能等于半径较大的圆. 这是什么?

让我们追踪每个圆点从红线起行到终点的路径. 将指向线上移动指向指向圆的半径,同时监测小圆从起行到终行行走的轨迹.

然后追踪一个大圆从头到尾的行走轨迹. 显然,一个大圆圈上的点需要更长的轨迹,从而需要更长的路径,才能到达同样的点.

换句话说,你可以从下诺夫哥罗德到莫斯科去通过弗拉基米尔,也可以通过阿尔克汉格尔斯克或阿斯特拉可汗去. 从尼日尼到莫斯科的距离保持不变,但沿着这些路线所必须走的道路却相去甚远.

这就是人类最杰出的头脑所困惑的悖论的解释。

来源

资料来源:/用户/147。