1426
"Fractals"
Mysterious disorder history of fractals and their applications
Fractal geometry - an amazing branch of mathematics, which conceals the key to understanding nature. To learn how to draw fractals, how they sound, what they taste like and why it is impossible to measure the length of the coastline, read the article.
The most brilliant discoveries in science to radically change human life. Invented the vaccine could save millions of people, the creation of weapons, on the contrary, these life-consuming. More recently (in the scale of human evolution), we have learned to "tame" the electricity - and now can not imagine life without these handy devices that use electricity. But there are discoveries that few people attaches importance, although they also strongly influence our lives.
One of these "invisible" openings - fractals. You probably have heard this word to remember, but do you know what it means and how many interesting things hidden in this term?
In every man laid natural curiosity, the desire to know the world around him. And in this endeavor man tries to stick to the logic of judgment. Analyzing the processes taking place around him, he tries to find the logic of what is happening and to bring some regularity. The greatest minds on the planet occupied by the task. Roughly speaking, the scientists are looking for a pattern where it should not be. Nevertheless, even in the chaos you can find a connection between the events. And this connection - fractal. Our little daughter, four and a half years, is now in the wonderful age when the number of questions "Why?" Is many times the number of responses that adults have time to give. Not so long ago, considering the raised ground with a branch, the daughter suddenly noticed that this branch, with twigs and branches, she is like a tree. And, of course, continue to follow the usual question, "Why?", To which his parents had to find a simple explanation, the child can understand.
The observed similarity between separate branches of a child with a tree - it is a very accurate observation, which once again demonstrates the principle of recursive self-similarity in nature. Many organic and inorganic forms of naturally formed similarly. Clouds, sea shells, "house" snails, bark and tree crowns, circulatory system, and so on - all of these random shapes of objects can be described by fractal algorithm.

Benoit Mandelbrot father of fractal geometry
The word "fractal" appeared thanks to the brilliant scientist Benoit Mandelbrot (Benoît B. Mandelbrot).
He coined the term in the seventies of the last century, borrowing from the Latin word fractus, where it literally means "break" or "crushed." What is it? Today, the word "fractal" often taken to mean a graphic representation of the structure, which is on a larger scale similar to herself.
The mathematical basis for the emergence of the theory of fractals was laid many years before the birth of Benoit Mandelbrot, but she was able to develop only with the advent of computers. At the beginning of his scientific career Benoit worked in the Research Center at IBM. While employees of the center worked on the transmission of data over a distance. During the research scientists are faced with the problem of large loss occurring due to noise. Before Benoit was a difficult and very important task - to understand how to predict the occurrence of noise interference in electronic circuits where the statistical method is ineffective.
Looking through the results of measurements of noise, Mandelbrot noticed a strange pattern - graphic noise in different scales look the same. An identical pattern was observed regardless of whether it was the noise schedule for one day, a week or an hour. Value change graph scale, and the picture was repeated every time.

During the life of Benoit Mandelbrot has repeatedly said that he does not deal with the formulas and just playing with images. This man thought very vividly, and any algebraic problem translated to geometry, where, according to him, is always the right answer is obvious.
No wonder that a person with such a rich spatial imagination became the father of fractal geometry. After understanding the essence of fractals comes a time when you begin to study the pictures and try to understand the meaning of the strange pattern of twists.
Fractal image has no identical elements, but has similar at any scale. To build such an image with a highly detailed manual previously was impossible, it took a huge amount of computation. For example, the French mathematician Pierre Fatou Jose Louis (Pierre Joseph Louis Fatou) described a set of more than seventy years before the discovery of Benoit Mandelbrot. If we talk about the principles of self-similarity, it is mentioned about them in the works of Leibniz and Georg Cantor.

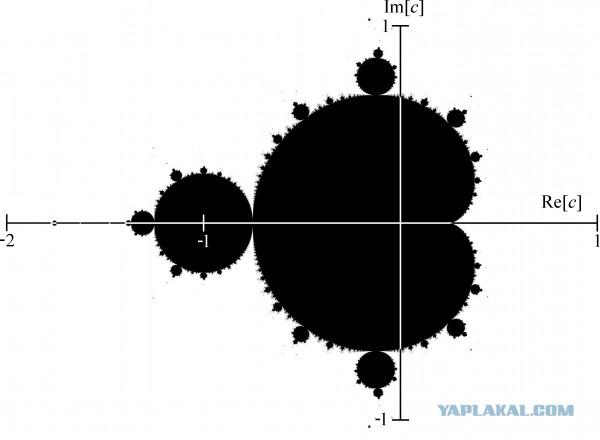
One of the first paintings were fractal graphic interpretation of the Mandelbrot set, which was born thanks to the research of Gaston Maurice Julia (Gaston Maurice Julia).
This French mathematician wondered how it will look a lot, if you build it on the basis of a simple formula, iterated loop feedback. If you explain the "fingers", which means that for a given number, we find the new value of the formula, and then substitute in formula again and obtain another value. The result - a large sequence of numbers.
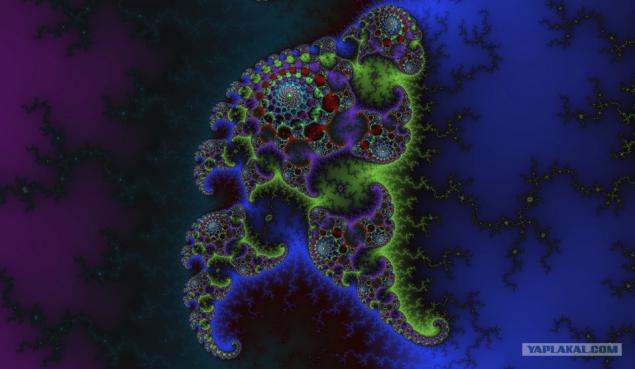
To get a complete picture of such a set, you need to do a huge amount of computing - hundreds, thousands, millions. Manually do this was simply unrealistic. But when mathematicians were at the disposal of powerful computing devices, they were able to take a fresh look at the formulas and expressions which have long aroused the interest. Mandelbrot was the first to use the computer to render the classic fractal. After processing sequence consisting of a large number of values, Benoit suffered results on a graph. That's what he got.
Subsequently, this image was painted (for example, one way of staining color - the number of iterations), and became one of the most popular images, which only have been created by man.

As the old saying, attributed to Heraclitus of Ephesus, "The same river can not enter twice." It is perfectly suited for the interpretation of the geometry of fractals. As much as we may have considered in detail a fractal image, all the time we'll see a similar pattern.
Posted in [mergetime] 1377776296 [/ mergetime]
Wishes to see how the image will look like the Mandelbrot space at multiple zooming can do so by downloading an animated GIF. 80Mb

Loren Carpenter: art, created by nature
The theory of fractals soon found practical application. Since it is closely linked with the visualization of self-similar images, it is not surprising that the first one who has adopted the principles of algorithms and unusual shapes, were artists.
Future co-founder of the legendary studio Pixar Lauren Carpenter (Loren C. Carpenter) in 1967 went to work for Boeing Computer Services, which was a division of the well-known corporation engaged in the development of new aircraft.
In 1977, he created a presentation with prototypes of flying models. The duties of Lorena was to develop planes projected image. He had to create images of new models showing future aircraft from different sides. At some point in the future the head of Pixar Animation Studios founder came up with the creative idea to use as a background image of the mountains. Today, this task can solve any student, but in the late seventies of the last century, computers could not cope with such complex calculations - graphic editors were not, not to mention the applications for three-dimensional graphics. In 1978, Lauren accidentally saw a book in the store Benoit Mandelbrot "Fractals: Form, and the dimension of an accident." In this book, his attention was drawn to the fact that Benoit cited many examples of fractal shapes in real life and to prove that they can be described by a mathematical expression.
This analogy was chosen not by chance that a mathematician. The fact is that as soon as he unveiled his studies, he had to face a barrage of criticism. The main thing is what is reproached his colleagues - the futility of the developed theory. "Yes, - they said - a beautiful picture, but no more. The practical value of the theory of fractals do not have. " There were also those who generally believe that fractal patterns - just by-products of "diabolical machine", which in the late seventies to many seemed to be something too complicated and unexplored to fully trust them. Mandelbrot was trying to find an obvious application of the theory of fractals, but, by and large, it did not need to do it. Followers of Benoit Mandelbrot in the next 25 years proved immensely from such a "mathematical curiosity," and Loren Carpenter was one of the first who tried the method of fractals in practice.

Having studied the book, the future animator seriously studied the principles of fractal geometry and began looking for a way to implement it in computer graphics. In just three days, Lauren was able to visualize a realistic image of the mountain system on your computer. In other words, he painted with formulas quite recognizable mountain landscape.

The principle that Lauren used to achieve the goal, was very simple. It consisted to divide larger geometrical figure into smaller elements, and those in turn, divided into a similar figure smaller.

Using larger triangles, Carpenter divide them into four small, and then repeating this process again and again until he could not get a realistic mountain landscape. Thus, he managed to become the first artist to apply in computer graphics fractal algorithm for imaging. Once it became aware of the work done, enthusiasts around the world picked up the idea and began to use fractal algorithms to simulate realistic natural forms.

Just a few years of their achievements Loren Carpenter was able to apply in a much more ambitious project. Animator created based on these two-minute demo Vol Libre, which was shown at Siggraph 1980. This video has shocked all who saw it, and Lauren received an invitation from Lucasfilm.
Animation render computer VAX-11/780 from Digital Equipment Corporation with a frequency of five megahertz, and drawing each frame took about half an hour.

Fractal Antenna: less is better
Over the past half-century life began to change rapidly. Most of us accept the achievements of modern technology for granted. To all that makes life more comfortable, you get used to very quickly. Few ask "Where did this come from?" And "How does it work?". Microwave heats breakfast - well, well, smart phone gives you the opportunity to talk with another person - great. It seems an obvious possibility.
But life would be totally different if people did not seek an explanation of events. Take, for example, cellular telephones. Remember retractable antenna on the first models? They prevented, increased the size of the device, in the end, often broke. We believe they all have sunk into oblivion, and partly the reason for it ... fractals.
Fractal patterns fascinate with their patterns. They definitely remind images of space objects - nebulae, clusters of galaxies, and so on. It is therefore quite natural that when Mandelbrot fractals voiced his theory, his research aroused intense interest among those who engaged in the study of astronomy. One of these lovers named Nathan Cohen (Nathan Cohen) after attending a lecture Benoit Mandelbrot in Budapest, hit on the idea of practical application of the knowledge gained. True, he did it intuitively, and not the last role played in its opening event. As a radio amateur, Nathan sought to create an antenna having the highest possible sensitivity.
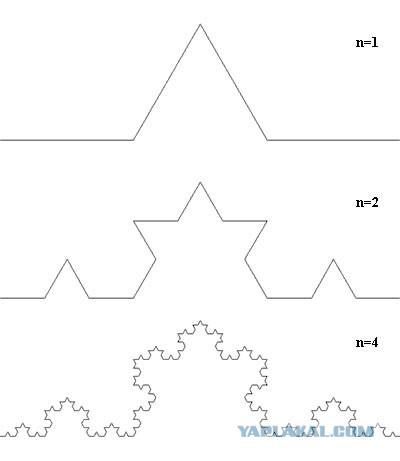
The only way to improve the parameters of the antenna, which was known at the time, is to increase its geometric dimensions. However, the owner of the property in the heart of Boston, which is rented Nathan, was strongly against the installation of large devices on the roof. Then Nathan began to experiment with various forms of antennas, trying to get maximum results with minimum dimensions. Inspired by the idea of fractal shapes, Cohen, as they say, blindly made of wire is one of the most famous fractals - "Koch snowflake." Swedish mathematician Helge von Koch (Helge von Koch) came up with this curve back in 1904. It is obtained by dividing the segment into three parts, and replacement of the middle segment of an equilateral triangle with no sides, which coincides with this segment. Determining a bit difficult to understand, but the figure everything is clear and simple.
When Nathan connect the antenna to the RF reception circuit, he was very surprised - sensitivity has increased dramatically. After a series of experiments, the future professor at Boston University, realized that the antenna is made of fractal pattern, it has a high efficiency and covers a much wider frequency range than the classic solutions. Furthermore, the shape of the antenna in the form of a fractal curve can significantly reduce the geometrical dimensions. Nathan Cohen even brought theorem proving that the creation of a broadband antenna is enough to give it the form of a self-similar fractal curve.
Author patented his discovery and founded the company in the development and design of fractal antenna Fractal Antenna Systems, believing that in the future thanks to his discovery of cell phones will be able to get rid of bulky antennas and become more compact.
Basically, what happened. However, to this day, Nathan is a legal battle with large corporations who illegally use his discovery for the production of compact communication devices. Some well-known manufacturers of mobile devices, such as, Motorola, have already come to a peace agreement with the inventor of fractal antenna.

Fractal dimensions: the mind can not understand
In his book, Mandelbrot tells of a very interesting mathematical paradox. The fifth chapter of the book "The Fractal Geometry of Nature" is dedicated, at first glance, a rather simple question: "What is the length of the coastline of Britain?" (A similar article was published it in the journal Science 1967).
This question Benoit borrowed from the famous American scholar Edward Kasner.
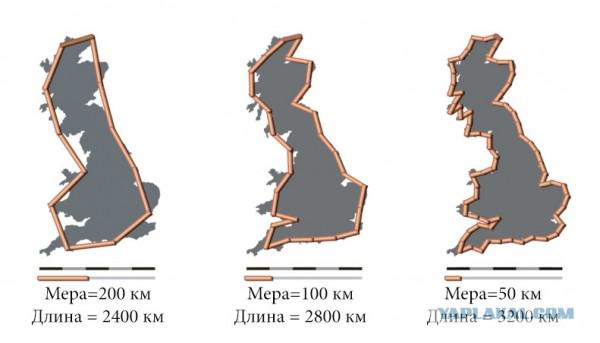
The latter, like many other famous mathematicians, loved to chat with the children by asking them questions and get surprising answers. Sometimes this led to surprising consequences. For example, a nine-year nephew Edward Kasner invented is now well known to all the word 'googol', denoting a unit with a hundred zeros. But back to fractals. American mathematician liked to ask the question, what is the length of the coastline of the United States. After hearing the opinion of the interlocutor, Edward himself told the correct answer. If we measure the length of the broken segments of the map, the result would be inaccurate, because the coastline has a large number of irregularities. And what will happen when measured as accurately as possible? We'll have to take into account the length of each irregularities - will need to measure every headland, every bay, rock, long rocky ledge, rock her, grains of sand, atoms and so on. As the number of irregularities tends to infinity, the measured length of the coastline is the measurement of each new irregularities increase to infinity.
Interestingly, following the prompts Edward faster adult children talking right decision, while the latter had a problem with the adoption of such an incredible response.
For example, this problem Mandelbrot proposed a new approach to measurement. Since the coastline close to the fractal curve, then we can apply characterizing parameter - the so-called fractal dimension.
What is the normal size - it is clear to anyone. If the dimension is equal to unity, we obtain a straight line, if two - flat shape, three - volume. However, such an understanding of the dimensions of mathematics does not work with fractal curves, where this parameter is a fractional value. The fractal dimension of mathematics can be conventionally regarded as "uneven." The higher the roughness curve, the higher its fractal dimension. The curve has at Mandelbrot fractal dimension higher than its topological dimension, has an approximate length of which does not depend on the number of measurements.
Now scientists are finding more and more areas to apply the theory of fractals.
Thanks to all.
and
Source:
Fractal geometry - an amazing branch of mathematics, which conceals the key to understanding nature. To learn how to draw fractals, how they sound, what they taste like and why it is impossible to measure the length of the coastline, read the article.

The most brilliant discoveries in science to radically change human life. Invented the vaccine could save millions of people, the creation of weapons, on the contrary, these life-consuming. More recently (in the scale of human evolution), we have learned to "tame" the electricity - and now can not imagine life without these handy devices that use electricity. But there are discoveries that few people attaches importance, although they also strongly influence our lives.
One of these "invisible" openings - fractals. You probably have heard this word to remember, but do you know what it means and how many interesting things hidden in this term?
In every man laid natural curiosity, the desire to know the world around him. And in this endeavor man tries to stick to the logic of judgment. Analyzing the processes taking place around him, he tries to find the logic of what is happening and to bring some regularity. The greatest minds on the planet occupied by the task. Roughly speaking, the scientists are looking for a pattern where it should not be. Nevertheless, even in the chaos you can find a connection between the events. And this connection - fractal. Our little daughter, four and a half years, is now in the wonderful age when the number of questions "Why?" Is many times the number of responses that adults have time to give. Not so long ago, considering the raised ground with a branch, the daughter suddenly noticed that this branch, with twigs and branches, she is like a tree. And, of course, continue to follow the usual question, "Why?", To which his parents had to find a simple explanation, the child can understand.
The observed similarity between separate branches of a child with a tree - it is a very accurate observation, which once again demonstrates the principle of recursive self-similarity in nature. Many organic and inorganic forms of naturally formed similarly. Clouds, sea shells, "house" snails, bark and tree crowns, circulatory system, and so on - all of these random shapes of objects can be described by fractal algorithm.

Benoit Mandelbrot father of fractal geometry
The word "fractal" appeared thanks to the brilliant scientist Benoit Mandelbrot (Benoît B. Mandelbrot).
He coined the term in the seventies of the last century, borrowing from the Latin word fractus, where it literally means "break" or "crushed." What is it? Today, the word "fractal" often taken to mean a graphic representation of the structure, which is on a larger scale similar to herself.
The mathematical basis for the emergence of the theory of fractals was laid many years before the birth of Benoit Mandelbrot, but she was able to develop only with the advent of computers. At the beginning of his scientific career Benoit worked in the Research Center at IBM. While employees of the center worked on the transmission of data over a distance. During the research scientists are faced with the problem of large loss occurring due to noise. Before Benoit was a difficult and very important task - to understand how to predict the occurrence of noise interference in electronic circuits where the statistical method is ineffective.
Looking through the results of measurements of noise, Mandelbrot noticed a strange pattern - graphic noise in different scales look the same. An identical pattern was observed regardless of whether it was the noise schedule for one day, a week or an hour. Value change graph scale, and the picture was repeated every time.

During the life of Benoit Mandelbrot has repeatedly said that he does not deal with the formulas and just playing with images. This man thought very vividly, and any algebraic problem translated to geometry, where, according to him, is always the right answer is obvious.
No wonder that a person with such a rich spatial imagination became the father of fractal geometry. After understanding the essence of fractals comes a time when you begin to study the pictures and try to understand the meaning of the strange pattern of twists.
Fractal image has no identical elements, but has similar at any scale. To build such an image with a highly detailed manual previously was impossible, it took a huge amount of computation. For example, the French mathematician Pierre Fatou Jose Louis (Pierre Joseph Louis Fatou) described a set of more than seventy years before the discovery of Benoit Mandelbrot. If we talk about the principles of self-similarity, it is mentioned about them in the works of Leibniz and Georg Cantor.

One of the first paintings were fractal graphic interpretation of the Mandelbrot set, which was born thanks to the research of Gaston Maurice Julia (Gaston Maurice Julia).
This French mathematician wondered how it will look a lot, if you build it on the basis of a simple formula, iterated loop feedback. If you explain the "fingers", which means that for a given number, we find the new value of the formula, and then substitute in formula again and obtain another value. The result - a large sequence of numbers.
To get a complete picture of such a set, you need to do a huge amount of computing - hundreds, thousands, millions. Manually do this was simply unrealistic. But when mathematicians were at the disposal of powerful computing devices, they were able to take a fresh look at the formulas and expressions which have long aroused the interest. Mandelbrot was the first to use the computer to render the classic fractal. After processing sequence consisting of a large number of values, Benoit suffered results on a graph. That's what he got.

Subsequently, this image was painted (for example, one way of staining color - the number of iterations), and became one of the most popular images, which only have been created by man.

As the old saying, attributed to Heraclitus of Ephesus, "The same river can not enter twice." It is perfectly suited for the interpretation of the geometry of fractals. As much as we may have considered in detail a fractal image, all the time we'll see a similar pattern.
Posted in [mergetime] 1377776296 [/ mergetime]
Wishes to see how the image will look like the Mandelbrot space at multiple zooming can do so by downloading an animated GIF. 80Mb

Loren Carpenter: art, created by nature
The theory of fractals soon found practical application. Since it is closely linked with the visualization of self-similar images, it is not surprising that the first one who has adopted the principles of algorithms and unusual shapes, were artists.
Future co-founder of the legendary studio Pixar Lauren Carpenter (Loren C. Carpenter) in 1967 went to work for Boeing Computer Services, which was a division of the well-known corporation engaged in the development of new aircraft.
In 1977, he created a presentation with prototypes of flying models. The duties of Lorena was to develop planes projected image. He had to create images of new models showing future aircraft from different sides. At some point in the future the head of Pixar Animation Studios founder came up with the creative idea to use as a background image of the mountains. Today, this task can solve any student, but in the late seventies of the last century, computers could not cope with such complex calculations - graphic editors were not, not to mention the applications for three-dimensional graphics. In 1978, Lauren accidentally saw a book in the store Benoit Mandelbrot "Fractals: Form, and the dimension of an accident." In this book, his attention was drawn to the fact that Benoit cited many examples of fractal shapes in real life and to prove that they can be described by a mathematical expression.
This analogy was chosen not by chance that a mathematician. The fact is that as soon as he unveiled his studies, he had to face a barrage of criticism. The main thing is what is reproached his colleagues - the futility of the developed theory. "Yes, - they said - a beautiful picture, but no more. The practical value of the theory of fractals do not have. " There were also those who generally believe that fractal patterns - just by-products of "diabolical machine", which in the late seventies to many seemed to be something too complicated and unexplored to fully trust them. Mandelbrot was trying to find an obvious application of the theory of fractals, but, by and large, it did not need to do it. Followers of Benoit Mandelbrot in the next 25 years proved immensely from such a "mathematical curiosity," and Loren Carpenter was one of the first who tried the method of fractals in practice.

Having studied the book, the future animator seriously studied the principles of fractal geometry and began looking for a way to implement it in computer graphics. In just three days, Lauren was able to visualize a realistic image of the mountain system on your computer. In other words, he painted with formulas quite recognizable mountain landscape.

The principle that Lauren used to achieve the goal, was very simple. It consisted to divide larger geometrical figure into smaller elements, and those in turn, divided into a similar figure smaller.

Using larger triangles, Carpenter divide them into four small, and then repeating this process again and again until he could not get a realistic mountain landscape. Thus, he managed to become the first artist to apply in computer graphics fractal algorithm for imaging. Once it became aware of the work done, enthusiasts around the world picked up the idea and began to use fractal algorithms to simulate realistic natural forms.

Just a few years of their achievements Loren Carpenter was able to apply in a much more ambitious project. Animator created based on these two-minute demo Vol Libre, which was shown at Siggraph 1980. This video has shocked all who saw it, and Lauren received an invitation from Lucasfilm.
Animation render computer VAX-11/780 from Digital Equipment Corporation with a frequency of five megahertz, and drawing each frame took about half an hour.

Fractal Antenna: less is better
Over the past half-century life began to change rapidly. Most of us accept the achievements of modern technology for granted. To all that makes life more comfortable, you get used to very quickly. Few ask "Where did this come from?" And "How does it work?". Microwave heats breakfast - well, well, smart phone gives you the opportunity to talk with another person - great. It seems an obvious possibility.
But life would be totally different if people did not seek an explanation of events. Take, for example, cellular telephones. Remember retractable antenna on the first models? They prevented, increased the size of the device, in the end, often broke. We believe they all have sunk into oblivion, and partly the reason for it ... fractals.
Fractal patterns fascinate with their patterns. They definitely remind images of space objects - nebulae, clusters of galaxies, and so on. It is therefore quite natural that when Mandelbrot fractals voiced his theory, his research aroused intense interest among those who engaged in the study of astronomy. One of these lovers named Nathan Cohen (Nathan Cohen) after attending a lecture Benoit Mandelbrot in Budapest, hit on the idea of practical application of the knowledge gained. True, he did it intuitively, and not the last role played in its opening event. As a radio amateur, Nathan sought to create an antenna having the highest possible sensitivity.
The only way to improve the parameters of the antenna, which was known at the time, is to increase its geometric dimensions. However, the owner of the property in the heart of Boston, which is rented Nathan, was strongly against the installation of large devices on the roof. Then Nathan began to experiment with various forms of antennas, trying to get maximum results with minimum dimensions. Inspired by the idea of fractal shapes, Cohen, as they say, blindly made of wire is one of the most famous fractals - "Koch snowflake." Swedish mathematician Helge von Koch (Helge von Koch) came up with this curve back in 1904. It is obtained by dividing the segment into three parts, and replacement of the middle segment of an equilateral triangle with no sides, which coincides with this segment. Determining a bit difficult to understand, but the figure everything is clear and simple.

When Nathan connect the antenna to the RF reception circuit, he was very surprised - sensitivity has increased dramatically. After a series of experiments, the future professor at Boston University, realized that the antenna is made of fractal pattern, it has a high efficiency and covers a much wider frequency range than the classic solutions. Furthermore, the shape of the antenna in the form of a fractal curve can significantly reduce the geometrical dimensions. Nathan Cohen even brought theorem proving that the creation of a broadband antenna is enough to give it the form of a self-similar fractal curve.
Author patented his discovery and founded the company in the development and design of fractal antenna Fractal Antenna Systems, believing that in the future thanks to his discovery of cell phones will be able to get rid of bulky antennas and become more compact.
Basically, what happened. However, to this day, Nathan is a legal battle with large corporations who illegally use his discovery for the production of compact communication devices. Some well-known manufacturers of mobile devices, such as, Motorola, have already come to a peace agreement with the inventor of fractal antenna.

Fractal dimensions: the mind can not understand
In his book, Mandelbrot tells of a very interesting mathematical paradox. The fifth chapter of the book "The Fractal Geometry of Nature" is dedicated, at first glance, a rather simple question: "What is the length of the coastline of Britain?" (A similar article was published it in the journal Science 1967).
This question Benoit borrowed from the famous American scholar Edward Kasner.
The latter, like many other famous mathematicians, loved to chat with the children by asking them questions and get surprising answers. Sometimes this led to surprising consequences. For example, a nine-year nephew Edward Kasner invented is now well known to all the word 'googol', denoting a unit with a hundred zeros. But back to fractals. American mathematician liked to ask the question, what is the length of the coastline of the United States. After hearing the opinion of the interlocutor, Edward himself told the correct answer. If we measure the length of the broken segments of the map, the result would be inaccurate, because the coastline has a large number of irregularities. And what will happen when measured as accurately as possible? We'll have to take into account the length of each irregularities - will need to measure every headland, every bay, rock, long rocky ledge, rock her, grains of sand, atoms and so on. As the number of irregularities tends to infinity, the measured length of the coastline is the measurement of each new irregularities increase to infinity.

Interestingly, following the prompts Edward faster adult children talking right decision, while the latter had a problem with the adoption of such an incredible response.
For example, this problem Mandelbrot proposed a new approach to measurement. Since the coastline close to the fractal curve, then we can apply characterizing parameter - the so-called fractal dimension.
What is the normal size - it is clear to anyone. If the dimension is equal to unity, we obtain a straight line, if two - flat shape, three - volume. However, such an understanding of the dimensions of mathematics does not work with fractal curves, where this parameter is a fractional value. The fractal dimension of mathematics can be conventionally regarded as "uneven." The higher the roughness curve, the higher its fractal dimension. The curve has at Mandelbrot fractal dimension higher than its topological dimension, has an approximate length of which does not depend on the number of measurements.
Now scientists are finding more and more areas to apply the theory of fractals.
Thanks to all.
and
Source:























