1430
“分形”
分形及其应用的神秘疾病史
分形几何 - 一个惊人的数学分支,它掩盖了关键认识自然。要了解如何绘制分形,他们是如何健全,他们味道,为什么它是无法衡量的海岸线长度,阅读文章。
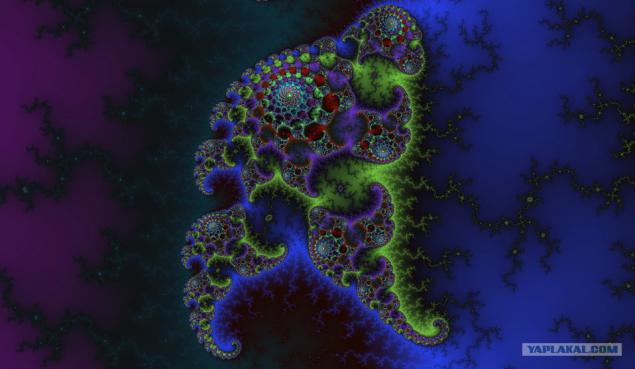
最辉煌的发现在科学,从根本上改变人类的生活。发明了疫苗可以挽救数以百万计的人,创造武器,相反,这些生活消费。最近(在人类进化的规模),我们已经学会了“驯服”电 - 现在无法想象生活中没有使用电这些方便的设备。但也有发现,很少人重视,虽然他们也强烈地影响着我们的生活。
其中的一个“隐形”开口 - 分形。您可能听说过这个词记住,但你知道这意味着什么,有多少隐藏在这个学期有趣的事情?
在每个人奠定了天生的好奇心,渴望了解他周围的世界。而在这方面男子试图坚持判断的逻辑。在分析过程中发生在他周围,他试图找到正在发生的事情的逻辑,并带来一定的规律性。在这个星球上最伟大的头脑占用的任务。粗略地说,科学家们正在寻找一种模式,它应该不会。然而,即使在混乱中可以找到的事件之间的连接。而这个连接 - 分形。我们的小女儿,四年半的时间,现在在美妙的时代,当问题的数量“为什么?”是的大人有时间作出响应很多的次数。不久前,考虑与一个分支升起的接地,女儿突然发现,这个分支,树枝和树枝,她就像是一棵树。当然,继续按照通常的问题:“为什么?”,对此他的父母不得不找到一个简单的解释,孩子能理解。
一个孩子一棵树单独的分支所观察到的相似性 - 这是一个非常准确的观察,这再次证明了递归自相似性的原则。许多有机和无机形式自然形成的类似。云,海贝壳,“房子”蜗牛,树皮和树冠,循环系统,等等 - 所有对象的这些随机的形状可以通过分形算法来描述。

蒙德布罗特父亲的分形几何
单词“分形”出现要归功于出色的科学家蒙德布罗特(伯努瓦B.曼德尔布罗)。
他创造了这个词在上世纪七十年代,来自拉丁词Fractus的,它的字面意思是“破发”或借“粉碎”。这是什么?今天,单词“分形”通常用来表示的结构,这是在更大的规模类似于她自己的图形表示。
为分形理论的出现的数学基础奠定了多年蒙德布罗特诞生之前,但她能够与计算机的出现只是发展。在他的科学生涯的开始伯努瓦曾在研究中心的IBM。而中心的雇员的数据的一段距离的发送工作。在研究过程中科学家们都面临着发生因噪音大的损失的问题。在贝努瓦是一个艰难的,非常重要的任务 - 要了解如何预测在电子电路中的统计方法是无效的噪音干扰的发生
。 综观噪声的测量结果,曼德勃罗注意到一个奇怪的模式 - 在不同的尺度图形噪声看起来是一样的。观察不管它是否是噪声日程一天,一周或一小时的相同的图案。价值变化曲线图规模,画面重复每次。

在蒙德布罗特的生活曾多次表示,他不处理的公式,只是玩的图像。这个人想得很生动,任何代数问题转化为几何,在那里,据他说,是永远正确的答案是显而易见的。
也难怪,一个人有如此丰富的空间想象成为分形几何之父。理解分形的本质后,来的时候,你开始学习的图片,并尝试了解的曲折奇特图案的含义的时候。
分形图像没有相同的元素,但在任何规模相似。要建立一个非常详细的手册,这样的形象在以前是不可能的,花了巨大的计算量。例如,法国数学家皮埃尔·法图何塞·路易斯(皮埃尔·约瑟夫·路易斯·法图)描述了一套七十多蒙德布罗特的发现之前。如果我们谈论的自相似原理,它是在莱布尼兹和康托尔的作品中提到他们。

其中的第一个作品都是Mandelbrot集,它诞生得益于加斯顿朱莉娅·莫里斯(莫里斯·加斯顿朱莉娅)的研究分形图形的解释。
这个法国数学家不知道怎么会好看很多,如果你一个简单的公式的基础上建设社会主义,迭代循环反馈。如果解释的“手指”,这意味着,对于给定的数,我们发现式的新的值,则替换式再次,将获得另一个值。结果 - 号的大序列
。 为了得到这样一组完整的图片,你需要做大量的计算 - 几百,几千,几百万。做手工,这是根本不现实的。但是,当数学家的处置强大的计算设备,他们能够重新审视的公式和表现形式早就引起了关注。曼德尔布罗是第一个用电脑来呈现经典的分形。处理序列组成的庞大数量的值后,伯努瓦遭遇上的曲线图的结果。这就是他了。
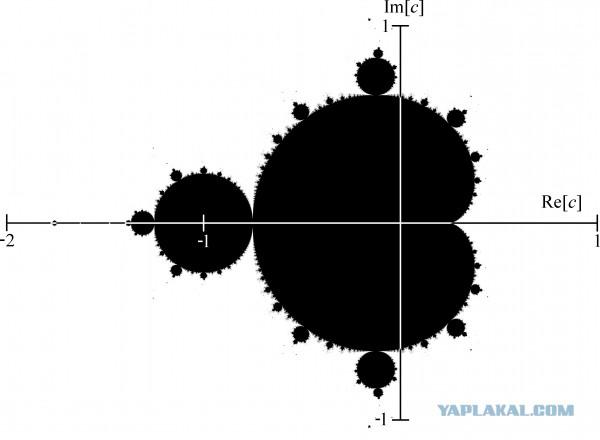
接着,该图像被画(例如,染色色的单程 - 迭代次数),和成为最流行的图像,这只是已创建人之一。

古语说,由于以弗所赫拉克利特,“同一条河流不能输入两次。”它非常适合于分形几何的解释。尽管我们可能已经在详细考虑一个分形图像,所有的时间,我们会看到一个类似的模式。
发表在[mergetime] 1377776296 [/ mergetime]
希望看到的图像会怎么看起来像在多个变焦的曼德尔布罗空间可以通过下载一个GIF动画这么做。 80MB

洛伦·卡彭特:艺术,大自然
创建
分形理论很快就找到了实际应用。既然是紧密结合的自相似图像可视化链接,这并不奇怪,谁已通过算法和不寻常的形状的原则,第一个,是艺术家。
传说工作室皮克斯劳伦匠(洛伦C.木匠)在1967年的未来共同创始人去工作,波音计算机服务,这是从事新型飞机的研制知名公司的一个部门。
1977年,他创建的演示文稿具有飞行模式的原型。洛雷娜的职责是开发平面投影图像。他创建的新车型呈现出从不同的侧面未来飞机的图像。在未来的某个时候皮克斯动画工作室创始人的头想出了一个创意,如同山上的背景图像使用。如今,这个任务可以解决任何学生,但在上世纪七十年代末,电脑无法应付如此复杂的计算 - 图形编辑器没有,更不要说为三维图形的应用程序。 1978年,劳伦无意间看到一本书,在商店蒙德布罗特“分形:形态,和事故的维度”在这本书中,他提请注意的是,伯努瓦引用在现实生活中,并证明他们可以通过一个数学表达式来描述分形形状的例子很多。
这个比喻被选择不是偶然的,一个数学家。事实是,只要他公布了他的研究,他不得不面对的批评攻势。最主要的是什么指责他的同事 - 发达理论是徒劳的。 “是的, - 他们说 - 一幅美丽的图画,但仅此而已。分形理论的实践价值没有“。也有那些谁普遍认为,分形图案 - 只是副产品“恶魔机器”,这在七十年代末到许多似乎是一些过于复杂,未开发的完全信任他们。曼德尔布罗试图找到分形理论的一个明显的应用程序,但是,总的来说,它并不需要这么做。蒙德布罗特在未来25年的追随者证明了极大从这样的“数学的好奇心,”和洛伦·卡彭特是第一个谁试图分形方法在实践中的一个。

在研究的书,未来动画师认真研究分形几何学的原理,并开始寻找一种方式在计算机图形来实现它。在短短的三天,劳伦是能够以可视化的山系的形象逼真的计算机上。换句话说,他画着公式相当知名的山地景观。

,劳伦用来实现这一目标的原则,很简单。它包括划分较大的几何图形成更小的元素,而这些反过来,分为类似的数字更小的。

使用较大的三角形,匠将其分为四个小,然后重复一遍又一遍这个过程,直到他无法得到一个现实的景观。因此,他成功地成为计算机图形学申请分形算法成像的第一位艺术家。一旦意识到所做的工作,在世界各地的爱好者拿起的想法,并开始用分形算法来模拟现实的自然形态。

短短几年间取得的成就洛伦·卡彭特的是能够在一个更加雄心勃勃的项目申请。动画创建基于这两分钟的演示卷自由报,这是在SIGGRAPH 1980年。这个视频带来的震撼所有谁看到它,劳伦接到卢卡斯的邀请。
动画渲染计算机VAX-11/780数字设备公司配备了主频五兆赫,并绘制每一帧花了约半小时。

分形天线:越少越好
在过去的半个世纪的生活开始迅速改变。我们大多数人接受现代科技的成果是理所当然的。为了所有,使生活更加舒适,你会习惯的速度非常快。很少有人问:“在哪里这是从哪里来的?”和“如何工作的?”。微波炉加热早餐 - 好,好,智能手机让你有机会与其他人交谈 - 伟大的。这似乎是一个明显的可能性。
但生活是完全不同的,如果人们不寻求事件的解释。举个例子来说,蜂窝式电话。记住伸缩天线上的第一款?它们阻止,增加了装置的尺寸,在结束时,经常破裂。我们相信,他们都陷入遗忘,部分因为它...分形的原因。
分形图案吸引他们的模式。他们绝对提醒的空间物体的图像 - 星云,星系团,等等。因此,它是很自然的,当曼德尔布罗分形表达了他的理论,他的研究引起了那些谁从事天文学研究的浓厚兴趣。其中一个恋人命名弥敦道科恩(内森·科恩)听课蒙德布罗特在布达佩斯后,打在所获得的知识的实际应用的想法。的确,他做到了直观,并在其开业活动不是最后的角色扮演。作为一名无线电爱好者,内森试图建立具有尽可能高的灵敏度的天线。
提高天线,这是已知的时间的参数的唯一方法,是为了提高其几何尺寸。然而,在波士顿的心脏,这是租来的内森物业的业主,强烈反对在屋顶大型设备安装。拿单开始尝试各种形式的天线,试图获得与最小尺寸最大的效果。分形的形状,科恩的想法的启发,正如他们所说的,盲目的做线是最有名的分形之一 - “科赫雪花”瑞典数学家黑尔格·冯·科赫(黑尔格·冯·科赫)想出了这个曲线回到1904年。它是通过将段得到的分为三部分,并更换一个等边三角形,无两侧,与本段重合的中间段。确定一个有点难以理解,但身材一切都简单明了。
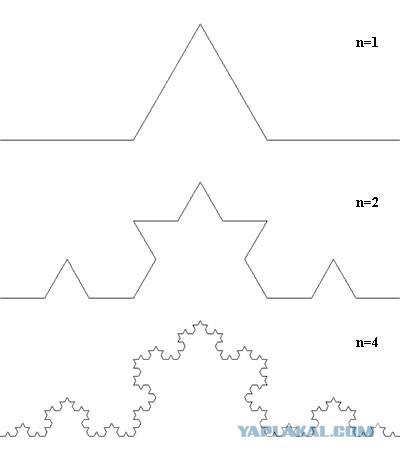
当内森将天线连接到射频接收电路,他非常惊讶 - 灵敏度显着增加。经过一系列的实验,在波士顿大学将来教授,意识到,天线是由分形图案,它具有较高的效率,并覆盖一个宽得多的频率范围比传统的解决方案。此外,在一分形曲线的形式的天线的形状可显著降低的几何尺寸。内森·科恩甚至还把定理证明,建立一个宽带天线就足以给它一个自相似的分形曲线的形式。
作者专利,他发现和创立的公司在发展和分形天线分形天线系统的设计,相信在他发现手机未来的感谢就能摆脱笨重的天线,变得更加紧凑。
基本上,发生了什么事。然而,到了今天,内森是非法使用他的发现为生产小型通信设备谁大公司一个法律战。一些知名厂商的移动设备,比如,摩托罗拉公司,都纷纷与分形天线的发明人达成和平协议。

分形尺寸:头脑无法理解
在他的书中,曼德勃罗讲述了一个非常有趣的数学悖论。书“分形几何性质”的第五章是专用的,乍一看,一个相当简单的问题:“什么是英国海岸线的长度”(类似文章发表就在科学杂志1967)
。 这个问题伯努瓦距离著名的美国学者爱德华·卡斯纳借来的。
后者,像其他许多著名的数学家,爱问他们的问题与孩子们聊天,并得到了惊人的答复。有时,这导致了令人惊讶的结果。例如,九年侄子爱德华卡斯纳发明现在众所周知的单词“固高',表示一个单元具有一百零。但是,回到分形。美国数学家喜欢问的问题,什么是美国的海岸线长度。听到对话者的意见后,爱德华亲口告诉正确答案。如果我们测量碎段的地图的长度,其结果将是不准确的,因为海岸线有大量的不规则性。当尽可能准确地测量会发生什么?我们必须考虑到每一个违规的长度 - 将需要衡量每一个岬角,每一个海湾,岩,长窜动,哄哄她,沙粒,原子等。作为凹凸的数目趋向于无穷大,海岸线的测量长度为每个新的凹凸的测量增加到无穷大。
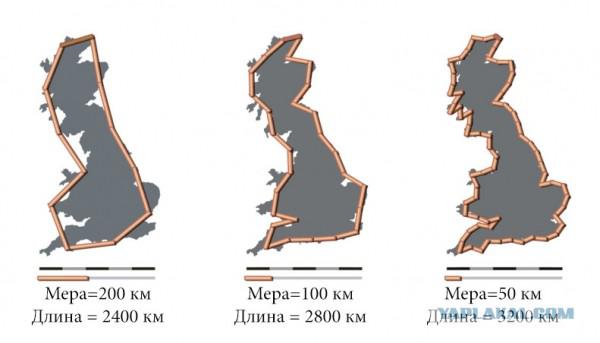
有趣的是,按照提示爱德华快成年的孩子讲正确的决定,而后者曾与通过这样一个令人难以置信的反应的问题。
例如,这个问题曼德尔布罗提出了一种新的方法来测量。由于海岸线接近的分形曲线,那么我们可以应用表征参数 - 即所谓的分形维数
。 这是正常尺寸 - 它是清楚的任何人。如果尺寸等于一,我们得到的直线,如果两个 - 扁平形状,三 - 体积。然而,数学的尺寸的这样的理解不与分形曲线,其中该参数是一个分数值工作。数学的分形维数可以被传统视为“不均衡。”较高的粗糙度曲线,它的分形维数越高。曲线具有比其拓扑维更高曼德尔布罗分形维数,具有的近似长度不依赖于测量的次数。
现在,科学家们发现越来越多的领域运用分形理论。
结论
谢谢。
资料来源:
分形几何 - 一个惊人的数学分支,它掩盖了关键认识自然。要了解如何绘制分形,他们是如何健全,他们味道,为什么它是无法衡量的海岸线长度,阅读文章。

最辉煌的发现在科学,从根本上改变人类的生活。发明了疫苗可以挽救数以百万计的人,创造武器,相反,这些生活消费。最近(在人类进化的规模),我们已经学会了“驯服”电 - 现在无法想象生活中没有使用电这些方便的设备。但也有发现,很少人重视,虽然他们也强烈地影响着我们的生活。
其中的一个“隐形”开口 - 分形。您可能听说过这个词记住,但你知道这意味着什么,有多少隐藏在这个学期有趣的事情?
在每个人奠定了天生的好奇心,渴望了解他周围的世界。而在这方面男子试图坚持判断的逻辑。在分析过程中发生在他周围,他试图找到正在发生的事情的逻辑,并带来一定的规律性。在这个星球上最伟大的头脑占用的任务。粗略地说,科学家们正在寻找一种模式,它应该不会。然而,即使在混乱中可以找到的事件之间的连接。而这个连接 - 分形。我们的小女儿,四年半的时间,现在在美妙的时代,当问题的数量“为什么?”是的大人有时间作出响应很多的次数。不久前,考虑与一个分支升起的接地,女儿突然发现,这个分支,树枝和树枝,她就像是一棵树。当然,继续按照通常的问题:“为什么?”,对此他的父母不得不找到一个简单的解释,孩子能理解。
一个孩子一棵树单独的分支所观察到的相似性 - 这是一个非常准确的观察,这再次证明了递归自相似性的原则。许多有机和无机形式自然形成的类似。云,海贝壳,“房子”蜗牛,树皮和树冠,循环系统,等等 - 所有对象的这些随机的形状可以通过分形算法来描述。

蒙德布罗特父亲的分形几何
单词“分形”出现要归功于出色的科学家蒙德布罗特(伯努瓦B.曼德尔布罗)。
他创造了这个词在上世纪七十年代,来自拉丁词Fractus的,它的字面意思是“破发”或借“粉碎”。这是什么?今天,单词“分形”通常用来表示的结构,这是在更大的规模类似于她自己的图形表示。
为分形理论的出现的数学基础奠定了多年蒙德布罗特诞生之前,但她能够与计算机的出现只是发展。在他的科学生涯的开始伯努瓦曾在研究中心的IBM。而中心的雇员的数据的一段距离的发送工作。在研究过程中科学家们都面临着发生因噪音大的损失的问题。在贝努瓦是一个艰难的,非常重要的任务 - 要了解如何预测在电子电路中的统计方法是无效的噪音干扰的发生
。 综观噪声的测量结果,曼德勃罗注意到一个奇怪的模式 - 在不同的尺度图形噪声看起来是一样的。观察不管它是否是噪声日程一天,一周或一小时的相同的图案。价值变化曲线图规模,画面重复每次。

在蒙德布罗特的生活曾多次表示,他不处理的公式,只是玩的图像。这个人想得很生动,任何代数问题转化为几何,在那里,据他说,是永远正确的答案是显而易见的。
也难怪,一个人有如此丰富的空间想象成为分形几何之父。理解分形的本质后,来的时候,你开始学习的图片,并尝试了解的曲折奇特图案的含义的时候。
分形图像没有相同的元素,但在任何规模相似。要建立一个非常详细的手册,这样的形象在以前是不可能的,花了巨大的计算量。例如,法国数学家皮埃尔·法图何塞·路易斯(皮埃尔·约瑟夫·路易斯·法图)描述了一套七十多蒙德布罗特的发现之前。如果我们谈论的自相似原理,它是在莱布尼兹和康托尔的作品中提到他们。

其中的第一个作品都是Mandelbrot集,它诞生得益于加斯顿朱莉娅·莫里斯(莫里斯·加斯顿朱莉娅)的研究分形图形的解释。
这个法国数学家不知道怎么会好看很多,如果你一个简单的公式的基础上建设社会主义,迭代循环反馈。如果解释的“手指”,这意味着,对于给定的数,我们发现式的新的值,则替换式再次,将获得另一个值。结果 - 号的大序列
。 为了得到这样一组完整的图片,你需要做大量的计算 - 几百,几千,几百万。做手工,这是根本不现实的。但是,当数学家的处置强大的计算设备,他们能够重新审视的公式和表现形式早就引起了关注。曼德尔布罗是第一个用电脑来呈现经典的分形。处理序列组成的庞大数量的值后,伯努瓦遭遇上的曲线图的结果。这就是他了。

接着,该图像被画(例如,染色色的单程 - 迭代次数),和成为最流行的图像,这只是已创建人之一。

古语说,由于以弗所赫拉克利特,“同一条河流不能输入两次。”它非常适合于分形几何的解释。尽管我们可能已经在详细考虑一个分形图像,所有的时间,我们会看到一个类似的模式。
发表在[mergetime] 1377776296 [/ mergetime]
希望看到的图像会怎么看起来像在多个变焦的曼德尔布罗空间可以通过下载一个GIF动画这么做。 80MB

洛伦·卡彭特:艺术,大自然
创建
分形理论很快就找到了实际应用。既然是紧密结合的自相似图像可视化链接,这并不奇怪,谁已通过算法和不寻常的形状的原则,第一个,是艺术家。
传说工作室皮克斯劳伦匠(洛伦C.木匠)在1967年的未来共同创始人去工作,波音计算机服务,这是从事新型飞机的研制知名公司的一个部门。
1977年,他创建的演示文稿具有飞行模式的原型。洛雷娜的职责是开发平面投影图像。他创建的新车型呈现出从不同的侧面未来飞机的图像。在未来的某个时候皮克斯动画工作室创始人的头想出了一个创意,如同山上的背景图像使用。如今,这个任务可以解决任何学生,但在上世纪七十年代末,电脑无法应付如此复杂的计算 - 图形编辑器没有,更不要说为三维图形的应用程序。 1978年,劳伦无意间看到一本书,在商店蒙德布罗特“分形:形态,和事故的维度”在这本书中,他提请注意的是,伯努瓦引用在现实生活中,并证明他们可以通过一个数学表达式来描述分形形状的例子很多。
这个比喻被选择不是偶然的,一个数学家。事实是,只要他公布了他的研究,他不得不面对的批评攻势。最主要的是什么指责他的同事 - 发达理论是徒劳的。 “是的, - 他们说 - 一幅美丽的图画,但仅此而已。分形理论的实践价值没有“。也有那些谁普遍认为,分形图案 - 只是副产品“恶魔机器”,这在七十年代末到许多似乎是一些过于复杂,未开发的完全信任他们。曼德尔布罗试图找到分形理论的一个明显的应用程序,但是,总的来说,它并不需要这么做。蒙德布罗特在未来25年的追随者证明了极大从这样的“数学的好奇心,”和洛伦·卡彭特是第一个谁试图分形方法在实践中的一个。

在研究的书,未来动画师认真研究分形几何学的原理,并开始寻找一种方式在计算机图形来实现它。在短短的三天,劳伦是能够以可视化的山系的形象逼真的计算机上。换句话说,他画着公式相当知名的山地景观。

,劳伦用来实现这一目标的原则,很简单。它包括划分较大的几何图形成更小的元素,而这些反过来,分为类似的数字更小的。

使用较大的三角形,匠将其分为四个小,然后重复一遍又一遍这个过程,直到他无法得到一个现实的景观。因此,他成功地成为计算机图形学申请分形算法成像的第一位艺术家。一旦意识到所做的工作,在世界各地的爱好者拿起的想法,并开始用分形算法来模拟现实的自然形态。

短短几年间取得的成就洛伦·卡彭特的是能够在一个更加雄心勃勃的项目申请。动画创建基于这两分钟的演示卷自由报,这是在SIGGRAPH 1980年。这个视频带来的震撼所有谁看到它,劳伦接到卢卡斯的邀请。
动画渲染计算机VAX-11/780数字设备公司配备了主频五兆赫,并绘制每一帧花了约半小时。

分形天线:越少越好
在过去的半个世纪的生活开始迅速改变。我们大多数人接受现代科技的成果是理所当然的。为了所有,使生活更加舒适,你会习惯的速度非常快。很少有人问:“在哪里这是从哪里来的?”和“如何工作的?”。微波炉加热早餐 - 好,好,智能手机让你有机会与其他人交谈 - 伟大的。这似乎是一个明显的可能性。
但生活是完全不同的,如果人们不寻求事件的解释。举个例子来说,蜂窝式电话。记住伸缩天线上的第一款?它们阻止,增加了装置的尺寸,在结束时,经常破裂。我们相信,他们都陷入遗忘,部分因为它...分形的原因。
分形图案吸引他们的模式。他们绝对提醒的空间物体的图像 - 星云,星系团,等等。因此,它是很自然的,当曼德尔布罗分形表达了他的理论,他的研究引起了那些谁从事天文学研究的浓厚兴趣。其中一个恋人命名弥敦道科恩(内森·科恩)听课蒙德布罗特在布达佩斯后,打在所获得的知识的实际应用的想法。的确,他做到了直观,并在其开业活动不是最后的角色扮演。作为一名无线电爱好者,内森试图建立具有尽可能高的灵敏度的天线。
提高天线,这是已知的时间的参数的唯一方法,是为了提高其几何尺寸。然而,在波士顿的心脏,这是租来的内森物业的业主,强烈反对在屋顶大型设备安装。拿单开始尝试各种形式的天线,试图获得与最小尺寸最大的效果。分形的形状,科恩的想法的启发,正如他们所说的,盲目的做线是最有名的分形之一 - “科赫雪花”瑞典数学家黑尔格·冯·科赫(黑尔格·冯·科赫)想出了这个曲线回到1904年。它是通过将段得到的分为三部分,并更换一个等边三角形,无两侧,与本段重合的中间段。确定一个有点难以理解,但身材一切都简单明了。

当内森将天线连接到射频接收电路,他非常惊讶 - 灵敏度显着增加。经过一系列的实验,在波士顿大学将来教授,意识到,天线是由分形图案,它具有较高的效率,并覆盖一个宽得多的频率范围比传统的解决方案。此外,在一分形曲线的形式的天线的形状可显著降低的几何尺寸。内森·科恩甚至还把定理证明,建立一个宽带天线就足以给它一个自相似的分形曲线的形式。
作者专利,他发现和创立的公司在发展和分形天线分形天线系统的设计,相信在他发现手机未来的感谢就能摆脱笨重的天线,变得更加紧凑。
基本上,发生了什么事。然而,到了今天,内森是非法使用他的发现为生产小型通信设备谁大公司一个法律战。一些知名厂商的移动设备,比如,摩托罗拉公司,都纷纷与分形天线的发明人达成和平协议。

分形尺寸:头脑无法理解
在他的书中,曼德勃罗讲述了一个非常有趣的数学悖论。书“分形几何性质”的第五章是专用的,乍一看,一个相当简单的问题:“什么是英国海岸线的长度”(类似文章发表就在科学杂志1967)
。 这个问题伯努瓦距离著名的美国学者爱德华·卡斯纳借来的。
后者,像其他许多著名的数学家,爱问他们的问题与孩子们聊天,并得到了惊人的答复。有时,这导致了令人惊讶的结果。例如,九年侄子爱德华卡斯纳发明现在众所周知的单词“固高',表示一个单元具有一百零。但是,回到分形。美国数学家喜欢问的问题,什么是美国的海岸线长度。听到对话者的意见后,爱德华亲口告诉正确答案。如果我们测量碎段的地图的长度,其结果将是不准确的,因为海岸线有大量的不规则性。当尽可能准确地测量会发生什么?我们必须考虑到每一个违规的长度 - 将需要衡量每一个岬角,每一个海湾,岩,长窜动,哄哄她,沙粒,原子等。作为凹凸的数目趋向于无穷大,海岸线的测量长度为每个新的凹凸的测量增加到无穷大。

有趣的是,按照提示爱德华快成年的孩子讲正确的决定,而后者曾与通过这样一个令人难以置信的反应的问题。
例如,这个问题曼德尔布罗提出了一种新的方法来测量。由于海岸线接近的分形曲线,那么我们可以应用表征参数 - 即所谓的分形维数
。 这是正常尺寸 - 它是清楚的任何人。如果尺寸等于一,我们得到的直线,如果两个 - 扁平形状,三 - 体积。然而,数学的尺寸的这样的理解不与分形曲线,其中该参数是一个分数值工作。数学的分形维数可以被传统视为“不均衡。”较高的粗糙度曲线,它的分形维数越高。曲线具有比其拓扑维更高曼德尔布罗分形维数,具有的近似长度不依赖于测量的次数。
现在,科学家们发现越来越多的领域运用分形理论。
结论
谢谢。
资料来源:























