1430
"Fractales"
Historia trastorno misterioso de los fractales y sus aplicaciones
La geometría fractal - una rama de las matemáticas increíble, que oculta la clave para entender la naturaleza. Para aprender a dibujar fractales, cómo suenan, lo que ellos saben como y por qué es imposible medir la longitud de la línea de costa, leer el artículo.
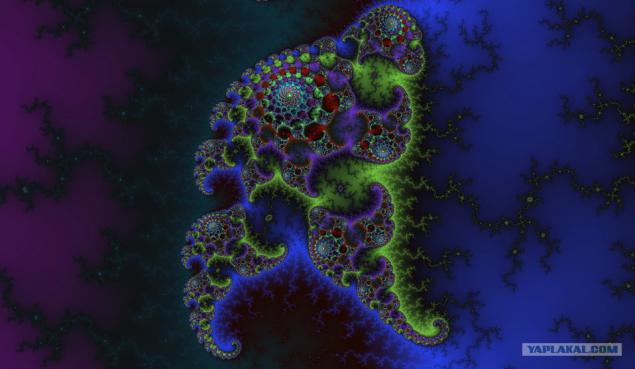
Los descubrimientos más brillantes de la ciencia para cambiar radicalmente la vida humana. Inventado la vacuna podría salvar a millones de personas, la creación de las armas, por el contrario, se trata de consumir la vida. Más recientemente (en la escala de la evolución humana), hemos aprendido a "domesticar" la electricidad - y ahora no puede imaginar la vida sin estos dispositivos de mano que utilizan electricidad. Pero hay descubrimientos que poca gente da importancia, aunque también influyen fuertemente en nuestras vidas.
Una de estas aberturas "invisibles" - fractales. Usted probablemente ha escuchado esta palabra para recordar, pero ¿sabe lo que significa y la cantidad de cosas interesantes ocultos en este término?
En toda la curiosidad natural del hombre relajado, el deseo de conocer el mundo que le rodea. Y en este esfuerzo el hombre trata de atenerse a la lógica del juicio. El análisis de los procesos que tienen lugar a su alrededor, trata de encontrar la lógica de lo que está pasando y para traer cierta regularidad. Las mentes más brillantes del planeta ocupados por la tarea. En términos generales, los científicos están buscando un patrón en el que no debe ser. Sin embargo, incluso en medio del caos se puede encontrar una conexión entre los eventos. Y esta conexión - fractal. Nuestra pequeña hija, de cuatro años y medio, se encuentra ahora en la era maravilloso cuando el número de preguntas "¿Por qué?" ¿Es muchas veces el número de respuestas que los adultos tienen tiempo para dar. No hace mucho tiempo, teniendo en cuenta el terreno enarbolado con una rama, la hija de repente se dio cuenta de que esta rama, con las ramitas y ramas, ella es como un árbol. Y, por supuesto, seguirá la pregunta de siempre: "¿Por qué?", A lo que sus padres tuvieron que encontrar una explicación simple, el niño puede entender.
La similitud observada entre ramas separadas de un niño con un árbol - es una observación muy precisa, lo que demuestra una vez más el principio de auto-similitud de naturaleza recursiva. Muchas formas orgánicas e inorgánicas de forma natural formado de manera similar. Nubes, conchas de mar, "casa" caracoles, corteza de árboles y coronas, sistema circulatorio, y así sucesivamente - todas estas formas aleatorias de objetos pueden ser descritos por el algoritmo fractal.

Benoit Mandelbrot padre de la geometría fractal
La palabra "fractal" apareció gracias a la brillante científico Benoit Mandelbrot (Benoît B. Mandelbrot).
Él acuñó el término en los años setenta del siglo pasado, los préstamos del fractus palabra latina, donde significa literalmente "break" o "aplastado". ¿Qué es? Hoy en día, la palabra "fractal" toma a menudo para referirse a una representación gráfica de la estructura, que es a mayor escala similar a sí misma.
La base matemática para el surgimiento de la teoría de los fractales se colocó muchos años antes del nacimiento de Benoit Mandelbrot, pero ella fue capaz de desarrollar sólo con el advenimiento de las computadoras. Al principio de su carrera científica Benoit trabajó en el Centro de Investigación de IBM. Mientras que los empleados del centro trabajaron en la transmisión de datos a través de una distancia. Durante los investigadores se enfrentan con el problema de la gran pérdida que ocurre debido al ruido. Antes de Benoit era una tarea difícil y muy importante - para entender cómo predecir la ocurrencia de interferencia de ruido en los circuitos electrónicos, donde el método estadístico es ineficaz
. Mirando a través de los resultados de las mediciones de ruido, Mandelbrot notó un extraño patrón - el ruido gráfica en diferentes escalas tienen el mismo aspecto. Un patrón idéntico se observó independientemente de si era el horario de ruido para un día, una semana o un horas. Cambio de valor de la escala gráfica, y la imagen se repitió cada vez.

Durante la vida de Benoit Mandelbrot ha dicho en repetidas ocasiones que él no se ocupa de las fórmulas y simplemente jugar con las imágenes. Este hombre pensó muy vívidamente, y cualquier problema algebraico traducido a la geometría, donde, según él, es siempre la respuesta correcta es obvia.
No es de extrañar que una persona con una rica imaginación tales espacial se convirtió en el padre de la geometría fractal. Después de comprender la esencia de los fractales llega un momento en que comience a estudiar las fotos y tratar de comprender el significado del extraño patrón de giros.
Imagen del fractal no tiene elementos idénticos, pero tiene similar en cualquier escala. Para construir una imagen de este tipo con un manual muy detallado anteriormente era imposible, tomó una enorme cantidad de cálculos. Por ejemplo, el matemático francés Pierre Fatou José Luis (Pierre Joseph Louis Fatou) describe un conjunto de más de setenta años antes del descubrimiento de Benoit Mandelbrot. Si hablamos de los principios de auto-similitud, se menciona acerca de ellos en la obra de Leibniz y Georg Cantor.

Una de las primeras pinturas eran interpretación gráfica fractal del conjunto de Mandelbrot, que nació gracias a la investigación de Gaston Maurice Julia (Gaston Maurice Julia).
Este matemático francés se preguntó cómo se verá mucho, si usted lo construye sobre la base de una fórmula simple, la retroalimentación de lazo reiteró. Si usted explica los "dedos", lo que significa que para un número dado, nos encontramos con el nuevo valor de la fórmula, y luego sustituimos en la fórmula una y obtenemos otro valor. El resultado - una gran secuencia de números
. Para obtener una imagen completa de un conjunto tal, que tiene que hacer una gran cantidad de computación - cientos, miles, millones. Manualmente qué esto era simplemente poco realista. Pero cuando los matemáticos estaban a disposición de potentes dispositivos informáticos, fueron capaces de tomar una nueva mirada a las fórmulas y expresiones que han despertado mucho interés. Mandelbrot fue el primero en utilizar el ordenador para hacer que el fractal clásico. Después de procesar la secuencia que consiste en un gran número de valores, Benoit sufrió resultados en una gráfica. Eso es lo que obtuvo.
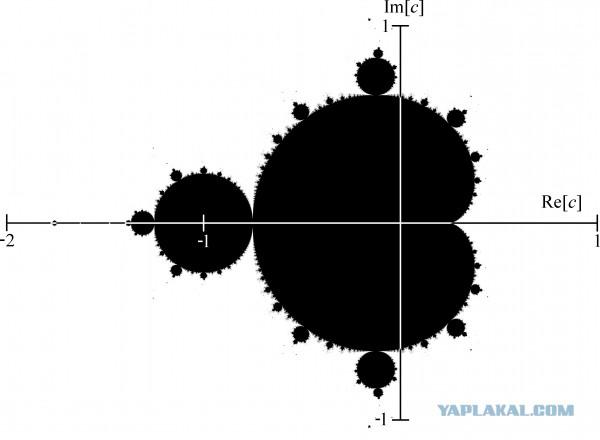
Posteriormente, esta imagen fue pintada (por ejemplo, una forma de color de tinción - el número de iteraciones), y se convirtió en una de las imágenes más populares, que sólo han sido creados por el hombre.

Como dice el viejo refrán, atribuida a Heráclito de Éfeso, "El mismo río no puede entrar dos veces." Está perfectamente adaptado para la interpretación de la geometría de los fractales. Por mucho que nos hayamos considerado en detalle una imagen fractal, todo el tiempo vamos a ver un patrón similar.
Publicado en [mergetime] 1377776296 [/ mergetime]
Deseos para ver cómo la imagen se verá como el espacio de Mandelbrot en múltiples zoom puede hacerlo mediante la descarga de un archivo GIF animado.
80Mb

Loren Carpintero: arte, creado por la naturaleza
La teoría de los fractales pronto se encontró aplicación práctica. Ya que está estrechamente relacionada con la visualización de imágenes auto-similares, no es de extrañar que la primera persona que ha adoptado los principios de algoritmos y formas inusuales, eran artistas.
Futuro cofundador del legendario estudio Pixar Lauren Carpenter (Loren C. Carpenter) en 1967 fue a trabajar para Boeing Computer Services, que era una división de la corporación conocida participan en el desarrollo de nuevos aviones.
En 1977, creó una presentación con prototipos de modelos de vuelo. Los deberes de Lorena fue desarrollar aviones imagen proyectada. Tuvo que crear imágenes de los nuevos modelos que muestran las futuras aeronaves desde diferentes lados. En algún momento en el futuro la cabeza del fundador de Pixar Animation Studios se le ocurrió la idea creativa para utilizar como imagen de fondo de las montañas. Hoy en día, esta tarea puede resolver cualquier estudiante, pero a finales de los años setenta del siglo pasado, las computadoras no podría hacer frente a este tipo de cálculos complejos - editores gráficos no eran, por no hablar de las aplicaciones para gráficos tridimensionales. En 1978, Lauren vio accidentalmente un libro en la tienda Benoit Mandelbrot "Fractales: Forma, y la dimensión de un accidente." En este libro, le llamó la atención al hecho de que Benoit citó muchos ejemplos de formas fractales en la vida real y para demostrar que pueden ser descritos por una expresión matemática.
Esta analogía fue elegido no por la posibilidad de que un matemático. El hecho es que tan pronto como se dio a conocer sus estudios, tuvo que enfrentarse a un aluvión de críticas. Lo más importante es lo que se reprocha a sus colegas - la futilidad de la teoría desarrollada. "Sí, - dijeron - un hermoso cuadro, pero no más. El valor práctico de la teoría de los fractales no tienen ". También hubo quienes en general creen que los patrones fractales - simplemente subproductos de "máquina diabólica", que a finales de los años setenta a muchos parecían ser algo demasiado complicado e inexplorado que confiar plenamente. Mandelbrot estaba tratando de encontrar una aplicación obvia de la teoría de los fractales, pero, en general, no tenía por qué hacerlo. Los seguidores de Benoit Mandelbrot en los próximos 25 años resultaron enormemente de un tal "curiosidad matemática", y Loren Carpenter, fue uno de los primeros que trató el método de fractales en la práctica.

Después de haber estudiado el libro, el animador futuro estudió seriamente los principios de la geometría fractal y comenzó a buscar una manera de ponerlo en práctica en gráficos por ordenador. En sólo tres días, Lauren fue capaz de visualizar una imagen realista del sistema montañoso en el equipo. En otras palabras, él pintó con fórmulas muy reconocible paisaje de montaña.

El principio de que Lauren utiliza para lograr el objetivo, era muy simple. Consistía dividir figura geométrica más grande en elementos más pequeños, y los que a su vez, dividido en una cifra similar más pequeño.

El uso de los triángulos más grandes, Carpintero dividirlos en cuatro pequeños, y luego repetir este proceso una y otra vez hasta que no pudo obtener un panorama realista de montaña. Por lo tanto, se las arregló para convertirse en el primer artista de aplicar en la infografía algoritmo fractal de imágenes. Una vez que se dio cuenta de los trabajos realizados, los aficionados de todo el mundo recogieron la idea y comenzaron a utilizar algoritmos fractales para simular las formas naturales realistas.

A pocos años de sus logros Loren Carpenter fue capaz de aplicar en un proyecto mucho más ambicioso. Animador creado en base a estos dos minutos de demostración Vol Libre, que fue mostrado en Siggraph 1980. Este video ha conmocionado a todo el que lo vio, y Lauren recibido una invitación de Lucasfilm.
Animación rendido computadora VAX-11/780 de Digital Equipment Corporation, con una frecuencia de cada cinco megahercios, y dibujando cada fotograma tarda una media hora.

Antena Fractal: menos es mejor
Durante el último medio siglo la vida comenzó a cambiar rápidamente. La mayoría de nosotros aceptamos los logros de la tecnología moderna por sentado. Para todo lo que hace la vida más cómoda, que te acostumbras a muy rápidamente. Pocos se preguntan "¿De dónde viene esto?" Y "¿Cómo funciona?". Microondas calienta el desayuno - bueno, bueno, teléfono inteligente le da la oportunidad de hablar con otra persona - grande. Parece una posibilidad obvia.
Pero la vida sería totalmente diferente si la gente no buscaron una explicación de los hechos. Tomemos, por ejemplo, los teléfonos celulares. Recuerde antena retráctil en los primeros modelos? Ellos prevenirse, aumentado el tamaño del dispositivo, en el extremo, a menudo se rompieron. Creemos que todos ellos han caído en el olvido, y en parte la razón para ello ... fractales.
Patrones fractales fascinan con sus patrones. Definitivamente, recuerdan las imágenes de los objetos espaciales - nebulosas, cúmulos de galaxias, y así sucesivamente. Por tanto, es muy natural que cuando los fractales de Mandelbrot expresaron su teoría, su investigación despertó gran interés entre los que participan en el estudio de la astronomía. Uno de estos amantes de nombre Nathan Cohen (Nathan Cohen) después de asistir a una conferencia Benoit Mandelbrot en Budapest, tuvo la idea de la aplicación práctica de los conocimientos adquiridos. Es cierto, lo hizo de manera intuitiva, y no el último papel jugó en su evento de apertura. Como radioaficionado, Nathan trató de crear una antena con la mayor sensibilidad posible.
La única manera de mejorar los parámetros de la antena, que se conocía en el momento, es aumentar sus dimensiones geométricas. Sin embargo, el dueño de la propiedad en el corazón de Boston, que se alquila Nathan, estaba fuertemente en contra de la instalación de grandes dispositivos de la azotea. Entonces Nathan comenzó a experimentar con las diversas formas de antenas, tratando de conseguir los máximos resultados con dimensiones mínimas. Inspirado en la idea de formas fractales, Cohen, como se suele decir, hecha ciegamente de alambre es uno de los más famosos fractales - "Koch copo de nieve". Matemático sueco Helge von Koch (Helge von Koch) se le ocurrió esta curva de nuevo en 1904. Se obtiene dividiendo el segmento en tres partes, y la sustitución del segmento medio de un triángulo equilátero con los lados, que coincide con este segmento. Determinar un poco difícil de entender, pero la cifra de todo es claro y simple.
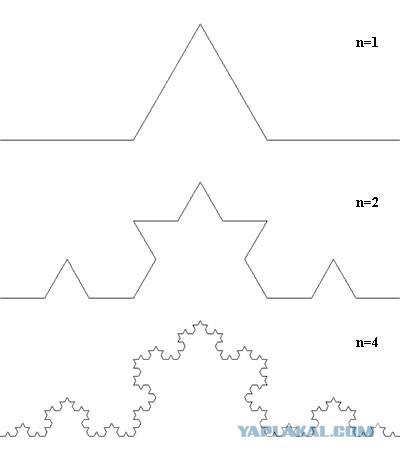
Cuando Nathan conectar la antena al circuito de recepción de RF, que estaba muy sorprendido - la sensibilidad se ha incrementado dramáticamente. Después de una serie de experimentos, el profesor de la Universidad de Boston futuro, dado cuenta de que la antena está hecha de patrón fractal, tiene una alta eficiencia y cubre una gama de frecuencias mucho más amplio que las soluciones clásicas. Además, la forma de la antena en la forma de una curva fractal puede reducir significativamente las dimensiones geométricas. Nathan Cohen incluso trajo teorema que demuestra que la creación de una antena de banda ancha es suficiente para darle la forma de una curva fractal auto-similar.
Autor patentó su descubrimiento y fundó la compañía en el desarrollo y diseño de antena fractal Fractal sistemas de antenas, en la creencia de que en el futuro gracias a su descubrimiento de teléfonos celulares será capaz de deshacerse de antenas voluminosos y ser más compacto.
Básicamente, lo que sucedió. Sin embargo, hasta este día, Nathan es una batalla legal con las grandes corporaciones que utilizan ilegalmente su descubrimiento para la producción de dispositivos de comunicación compactos. Algunos fabricantes bien conocidos de los dispositivos móviles, como por ejemplo, Motorola, ya han llegado a un acuerdo de paz con el inventor de la antena fractal.

Dimensiones fractales: la mente no puede entender
En su libro, Mandelbrot habla de un muy interesante paradoja matemática. El quinto capítulo del libro "La geometría fractal de la naturaleza" se dedica, a primera vista, una pregunta bastante simple: "¿Cuál es la longitud de la costa de Bretaña" (Un artículo similar se publicó en la revista Science 1967)
. Esta pregunta Benoit tomado del famoso erudito estadounidense Edward Kasner.
Este último, al igual que muchos otros famosos matemáticos, querido charlar con los niños haciéndoles preguntas y obtener respuestas sorprendentes. A veces esto llevó a consecuencias sorprendentes. Por ejemplo, un sobrino de nueve años Edward Kasner inventó es ahora bien conocido por todos la palabra 'googol', que denota una unidad con cien ceros. Pero volvamos a los fractales. Matemático estadounidense le gusta hacer la pregunta, ¿cuál es la longitud de la costa de los Estados Unidos. Después de escuchar la opinión del interlocutor, el propio Edward dijo a la respuesta correcta. Si medimos la longitud de los segmentos rotos del mapa, el resultado sería inexacto, ya que la costa tiene un gran número de irregularidades. ¿Y qué va a pasar cuando se mide con la mayor precisión posible? Tendremos que tener en cuenta la longitud de cada uno irregularidades - tendrá que medir cada punta, cada bahía, roca, larga saliente rocoso, mecerla, granos de arena, átomos y así sucesivamente. Como el número de irregularidades tiende a infinito, la longitud medida de la costa es la medición de cada nuevo irregularidades aumentar hasta el infinito.
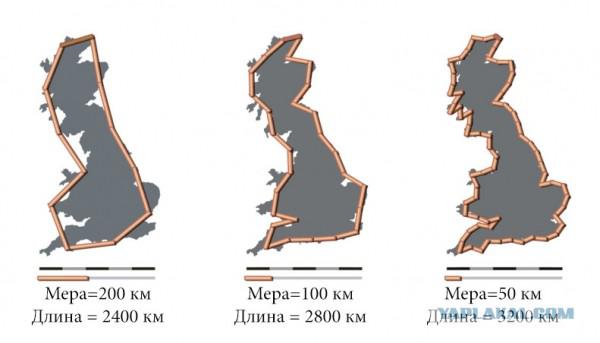
Curiosamente, siguiendo las instrucciones Edward niños más rápido adultos hablando decisión correcta, mientras que el segundo tenía un problema con la adopción de una respuesta tan increíble.
Por ejemplo, este problema Mandelbrot propuso un nuevo enfoque a la medición. Desde la costa cerca de la curva fractal, entonces podemos aplicar la caracterización de parámetros - la llamada dimensión fractal
. ¿Cuál es el tamaño normal - es claro para cualquiera. Si la dimensión es igual a la unidad, se obtiene una línea recta, si dos - forma plana, tres - volumen. Sin embargo, la comprensión de las dimensiones de las matemáticas tales no funciona con curvas fractales, donde este parámetro es un valor fraccionario. La dimensión fractal de las matemáticas puede ser considerado convencionalmente como "desigual." Cuanto mayor sea la curva de rugosidad, mayor es su dimensión fractal. La curva tiene al Mandelbrot dimensión fractal mayor que su dimensión topológica, tiene una longitud aproximada de las cuales no depende del número de mediciones.
Ahora los científicos están descubriendo más y más áreas de aplicar la teoría de los fractales.
Conclusión
y
Fuente:
La geometría fractal - una rama de las matemáticas increíble, que oculta la clave para entender la naturaleza. Para aprender a dibujar fractales, cómo suenan, lo que ellos saben como y por qué es imposible medir la longitud de la línea de costa, leer el artículo.

Los descubrimientos más brillantes de la ciencia para cambiar radicalmente la vida humana. Inventado la vacuna podría salvar a millones de personas, la creación de las armas, por el contrario, se trata de consumir la vida. Más recientemente (en la escala de la evolución humana), hemos aprendido a "domesticar" la electricidad - y ahora no puede imaginar la vida sin estos dispositivos de mano que utilizan electricidad. Pero hay descubrimientos que poca gente da importancia, aunque también influyen fuertemente en nuestras vidas.
Una de estas aberturas "invisibles" - fractales. Usted probablemente ha escuchado esta palabra para recordar, pero ¿sabe lo que significa y la cantidad de cosas interesantes ocultos en este término?
En toda la curiosidad natural del hombre relajado, el deseo de conocer el mundo que le rodea. Y en este esfuerzo el hombre trata de atenerse a la lógica del juicio. El análisis de los procesos que tienen lugar a su alrededor, trata de encontrar la lógica de lo que está pasando y para traer cierta regularidad. Las mentes más brillantes del planeta ocupados por la tarea. En términos generales, los científicos están buscando un patrón en el que no debe ser. Sin embargo, incluso en medio del caos se puede encontrar una conexión entre los eventos. Y esta conexión - fractal. Nuestra pequeña hija, de cuatro años y medio, se encuentra ahora en la era maravilloso cuando el número de preguntas "¿Por qué?" ¿Es muchas veces el número de respuestas que los adultos tienen tiempo para dar. No hace mucho tiempo, teniendo en cuenta el terreno enarbolado con una rama, la hija de repente se dio cuenta de que esta rama, con las ramitas y ramas, ella es como un árbol. Y, por supuesto, seguirá la pregunta de siempre: "¿Por qué?", A lo que sus padres tuvieron que encontrar una explicación simple, el niño puede entender.
La similitud observada entre ramas separadas de un niño con un árbol - es una observación muy precisa, lo que demuestra una vez más el principio de auto-similitud de naturaleza recursiva. Muchas formas orgánicas e inorgánicas de forma natural formado de manera similar. Nubes, conchas de mar, "casa" caracoles, corteza de árboles y coronas, sistema circulatorio, y así sucesivamente - todas estas formas aleatorias de objetos pueden ser descritos por el algoritmo fractal.

Benoit Mandelbrot padre de la geometría fractal
La palabra "fractal" apareció gracias a la brillante científico Benoit Mandelbrot (Benoît B. Mandelbrot).
Él acuñó el término en los años setenta del siglo pasado, los préstamos del fractus palabra latina, donde significa literalmente "break" o "aplastado". ¿Qué es? Hoy en día, la palabra "fractal" toma a menudo para referirse a una representación gráfica de la estructura, que es a mayor escala similar a sí misma.
La base matemática para el surgimiento de la teoría de los fractales se colocó muchos años antes del nacimiento de Benoit Mandelbrot, pero ella fue capaz de desarrollar sólo con el advenimiento de las computadoras. Al principio de su carrera científica Benoit trabajó en el Centro de Investigación de IBM. Mientras que los empleados del centro trabajaron en la transmisión de datos a través de una distancia. Durante los investigadores se enfrentan con el problema de la gran pérdida que ocurre debido al ruido. Antes de Benoit era una tarea difícil y muy importante - para entender cómo predecir la ocurrencia de interferencia de ruido en los circuitos electrónicos, donde el método estadístico es ineficaz
. Mirando a través de los resultados de las mediciones de ruido, Mandelbrot notó un extraño patrón - el ruido gráfica en diferentes escalas tienen el mismo aspecto. Un patrón idéntico se observó independientemente de si era el horario de ruido para un día, una semana o un horas. Cambio de valor de la escala gráfica, y la imagen se repitió cada vez.

Durante la vida de Benoit Mandelbrot ha dicho en repetidas ocasiones que él no se ocupa de las fórmulas y simplemente jugar con las imágenes. Este hombre pensó muy vívidamente, y cualquier problema algebraico traducido a la geometría, donde, según él, es siempre la respuesta correcta es obvia.
No es de extrañar que una persona con una rica imaginación tales espacial se convirtió en el padre de la geometría fractal. Después de comprender la esencia de los fractales llega un momento en que comience a estudiar las fotos y tratar de comprender el significado del extraño patrón de giros.
Imagen del fractal no tiene elementos idénticos, pero tiene similar en cualquier escala. Para construir una imagen de este tipo con un manual muy detallado anteriormente era imposible, tomó una enorme cantidad de cálculos. Por ejemplo, el matemático francés Pierre Fatou José Luis (Pierre Joseph Louis Fatou) describe un conjunto de más de setenta años antes del descubrimiento de Benoit Mandelbrot. Si hablamos de los principios de auto-similitud, se menciona acerca de ellos en la obra de Leibniz y Georg Cantor.

Una de las primeras pinturas eran interpretación gráfica fractal del conjunto de Mandelbrot, que nació gracias a la investigación de Gaston Maurice Julia (Gaston Maurice Julia).
Este matemático francés se preguntó cómo se verá mucho, si usted lo construye sobre la base de una fórmula simple, la retroalimentación de lazo reiteró. Si usted explica los "dedos", lo que significa que para un número dado, nos encontramos con el nuevo valor de la fórmula, y luego sustituimos en la fórmula una y obtenemos otro valor. El resultado - una gran secuencia de números
. Para obtener una imagen completa de un conjunto tal, que tiene que hacer una gran cantidad de computación - cientos, miles, millones. Manualmente qué esto era simplemente poco realista. Pero cuando los matemáticos estaban a disposición de potentes dispositivos informáticos, fueron capaces de tomar una nueva mirada a las fórmulas y expresiones que han despertado mucho interés. Mandelbrot fue el primero en utilizar el ordenador para hacer que el fractal clásico. Después de procesar la secuencia que consiste en un gran número de valores, Benoit sufrió resultados en una gráfica. Eso es lo que obtuvo.

Posteriormente, esta imagen fue pintada (por ejemplo, una forma de color de tinción - el número de iteraciones), y se convirtió en una de las imágenes más populares, que sólo han sido creados por el hombre.

Como dice el viejo refrán, atribuida a Heráclito de Éfeso, "El mismo río no puede entrar dos veces." Está perfectamente adaptado para la interpretación de la geometría de los fractales. Por mucho que nos hayamos considerado en detalle una imagen fractal, todo el tiempo vamos a ver un patrón similar.
Publicado en [mergetime] 1377776296 [/ mergetime]
Deseos para ver cómo la imagen se verá como el espacio de Mandelbrot en múltiples zoom puede hacerlo mediante la descarga de un archivo GIF animado.
80Mb

Loren Carpintero: arte, creado por la naturaleza
La teoría de los fractales pronto se encontró aplicación práctica. Ya que está estrechamente relacionada con la visualización de imágenes auto-similares, no es de extrañar que la primera persona que ha adoptado los principios de algoritmos y formas inusuales, eran artistas.
Futuro cofundador del legendario estudio Pixar Lauren Carpenter (Loren C. Carpenter) en 1967 fue a trabajar para Boeing Computer Services, que era una división de la corporación conocida participan en el desarrollo de nuevos aviones.
En 1977, creó una presentación con prototipos de modelos de vuelo. Los deberes de Lorena fue desarrollar aviones imagen proyectada. Tuvo que crear imágenes de los nuevos modelos que muestran las futuras aeronaves desde diferentes lados. En algún momento en el futuro la cabeza del fundador de Pixar Animation Studios se le ocurrió la idea creativa para utilizar como imagen de fondo de las montañas. Hoy en día, esta tarea puede resolver cualquier estudiante, pero a finales de los años setenta del siglo pasado, las computadoras no podría hacer frente a este tipo de cálculos complejos - editores gráficos no eran, por no hablar de las aplicaciones para gráficos tridimensionales. En 1978, Lauren vio accidentalmente un libro en la tienda Benoit Mandelbrot "Fractales: Forma, y la dimensión de un accidente." En este libro, le llamó la atención al hecho de que Benoit citó muchos ejemplos de formas fractales en la vida real y para demostrar que pueden ser descritos por una expresión matemática.
Esta analogía fue elegido no por la posibilidad de que un matemático. El hecho es que tan pronto como se dio a conocer sus estudios, tuvo que enfrentarse a un aluvión de críticas. Lo más importante es lo que se reprocha a sus colegas - la futilidad de la teoría desarrollada. "Sí, - dijeron - un hermoso cuadro, pero no más. El valor práctico de la teoría de los fractales no tienen ". También hubo quienes en general creen que los patrones fractales - simplemente subproductos de "máquina diabólica", que a finales de los años setenta a muchos parecían ser algo demasiado complicado e inexplorado que confiar plenamente. Mandelbrot estaba tratando de encontrar una aplicación obvia de la teoría de los fractales, pero, en general, no tenía por qué hacerlo. Los seguidores de Benoit Mandelbrot en los próximos 25 años resultaron enormemente de un tal "curiosidad matemática", y Loren Carpenter, fue uno de los primeros que trató el método de fractales en la práctica.

Después de haber estudiado el libro, el animador futuro estudió seriamente los principios de la geometría fractal y comenzó a buscar una manera de ponerlo en práctica en gráficos por ordenador. En sólo tres días, Lauren fue capaz de visualizar una imagen realista del sistema montañoso en el equipo. En otras palabras, él pintó con fórmulas muy reconocible paisaje de montaña.

El principio de que Lauren utiliza para lograr el objetivo, era muy simple. Consistía dividir figura geométrica más grande en elementos más pequeños, y los que a su vez, dividido en una cifra similar más pequeño.

El uso de los triángulos más grandes, Carpintero dividirlos en cuatro pequeños, y luego repetir este proceso una y otra vez hasta que no pudo obtener un panorama realista de montaña. Por lo tanto, se las arregló para convertirse en el primer artista de aplicar en la infografía algoritmo fractal de imágenes. Una vez que se dio cuenta de los trabajos realizados, los aficionados de todo el mundo recogieron la idea y comenzaron a utilizar algoritmos fractales para simular las formas naturales realistas.

A pocos años de sus logros Loren Carpenter fue capaz de aplicar en un proyecto mucho más ambicioso. Animador creado en base a estos dos minutos de demostración Vol Libre, que fue mostrado en Siggraph 1980. Este video ha conmocionado a todo el que lo vio, y Lauren recibido una invitación de Lucasfilm.
Animación rendido computadora VAX-11/780 de Digital Equipment Corporation, con una frecuencia de cada cinco megahercios, y dibujando cada fotograma tarda una media hora.

Antena Fractal: menos es mejor
Durante el último medio siglo la vida comenzó a cambiar rápidamente. La mayoría de nosotros aceptamos los logros de la tecnología moderna por sentado. Para todo lo que hace la vida más cómoda, que te acostumbras a muy rápidamente. Pocos se preguntan "¿De dónde viene esto?" Y "¿Cómo funciona?". Microondas calienta el desayuno - bueno, bueno, teléfono inteligente le da la oportunidad de hablar con otra persona - grande. Parece una posibilidad obvia.
Pero la vida sería totalmente diferente si la gente no buscaron una explicación de los hechos. Tomemos, por ejemplo, los teléfonos celulares. Recuerde antena retráctil en los primeros modelos? Ellos prevenirse, aumentado el tamaño del dispositivo, en el extremo, a menudo se rompieron. Creemos que todos ellos han caído en el olvido, y en parte la razón para ello ... fractales.
Patrones fractales fascinan con sus patrones. Definitivamente, recuerdan las imágenes de los objetos espaciales - nebulosas, cúmulos de galaxias, y así sucesivamente. Por tanto, es muy natural que cuando los fractales de Mandelbrot expresaron su teoría, su investigación despertó gran interés entre los que participan en el estudio de la astronomía. Uno de estos amantes de nombre Nathan Cohen (Nathan Cohen) después de asistir a una conferencia Benoit Mandelbrot en Budapest, tuvo la idea de la aplicación práctica de los conocimientos adquiridos. Es cierto, lo hizo de manera intuitiva, y no el último papel jugó en su evento de apertura. Como radioaficionado, Nathan trató de crear una antena con la mayor sensibilidad posible.
La única manera de mejorar los parámetros de la antena, que se conocía en el momento, es aumentar sus dimensiones geométricas. Sin embargo, el dueño de la propiedad en el corazón de Boston, que se alquila Nathan, estaba fuertemente en contra de la instalación de grandes dispositivos de la azotea. Entonces Nathan comenzó a experimentar con las diversas formas de antenas, tratando de conseguir los máximos resultados con dimensiones mínimas. Inspirado en la idea de formas fractales, Cohen, como se suele decir, hecha ciegamente de alambre es uno de los más famosos fractales - "Koch copo de nieve". Matemático sueco Helge von Koch (Helge von Koch) se le ocurrió esta curva de nuevo en 1904. Se obtiene dividiendo el segmento en tres partes, y la sustitución del segmento medio de un triángulo equilátero con los lados, que coincide con este segmento. Determinar un poco difícil de entender, pero la cifra de todo es claro y simple.

Cuando Nathan conectar la antena al circuito de recepción de RF, que estaba muy sorprendido - la sensibilidad se ha incrementado dramáticamente. Después de una serie de experimentos, el profesor de la Universidad de Boston futuro, dado cuenta de que la antena está hecha de patrón fractal, tiene una alta eficiencia y cubre una gama de frecuencias mucho más amplio que las soluciones clásicas. Además, la forma de la antena en la forma de una curva fractal puede reducir significativamente las dimensiones geométricas. Nathan Cohen incluso trajo teorema que demuestra que la creación de una antena de banda ancha es suficiente para darle la forma de una curva fractal auto-similar.
Autor patentó su descubrimiento y fundó la compañía en el desarrollo y diseño de antena fractal Fractal sistemas de antenas, en la creencia de que en el futuro gracias a su descubrimiento de teléfonos celulares será capaz de deshacerse de antenas voluminosos y ser más compacto.
Básicamente, lo que sucedió. Sin embargo, hasta este día, Nathan es una batalla legal con las grandes corporaciones que utilizan ilegalmente su descubrimiento para la producción de dispositivos de comunicación compactos. Algunos fabricantes bien conocidos de los dispositivos móviles, como por ejemplo, Motorola, ya han llegado a un acuerdo de paz con el inventor de la antena fractal.

Dimensiones fractales: la mente no puede entender
En su libro, Mandelbrot habla de un muy interesante paradoja matemática. El quinto capítulo del libro "La geometría fractal de la naturaleza" se dedica, a primera vista, una pregunta bastante simple: "¿Cuál es la longitud de la costa de Bretaña" (Un artículo similar se publicó en la revista Science 1967)
. Esta pregunta Benoit tomado del famoso erudito estadounidense Edward Kasner.
Este último, al igual que muchos otros famosos matemáticos, querido charlar con los niños haciéndoles preguntas y obtener respuestas sorprendentes. A veces esto llevó a consecuencias sorprendentes. Por ejemplo, un sobrino de nueve años Edward Kasner inventó es ahora bien conocido por todos la palabra 'googol', que denota una unidad con cien ceros. Pero volvamos a los fractales. Matemático estadounidense le gusta hacer la pregunta, ¿cuál es la longitud de la costa de los Estados Unidos. Después de escuchar la opinión del interlocutor, el propio Edward dijo a la respuesta correcta. Si medimos la longitud de los segmentos rotos del mapa, el resultado sería inexacto, ya que la costa tiene un gran número de irregularidades. ¿Y qué va a pasar cuando se mide con la mayor precisión posible? Tendremos que tener en cuenta la longitud de cada uno irregularidades - tendrá que medir cada punta, cada bahía, roca, larga saliente rocoso, mecerla, granos de arena, átomos y así sucesivamente. Como el número de irregularidades tiende a infinito, la longitud medida de la costa es la medición de cada nuevo irregularidades aumentar hasta el infinito.

Curiosamente, siguiendo las instrucciones Edward niños más rápido adultos hablando decisión correcta, mientras que el segundo tenía un problema con la adopción de una respuesta tan increíble.
Por ejemplo, este problema Mandelbrot propuso un nuevo enfoque a la medición. Desde la costa cerca de la curva fractal, entonces podemos aplicar la caracterización de parámetros - la llamada dimensión fractal
. ¿Cuál es el tamaño normal - es claro para cualquiera. Si la dimensión es igual a la unidad, se obtiene una línea recta, si dos - forma plana, tres - volumen. Sin embargo, la comprensión de las dimensiones de las matemáticas tales no funciona con curvas fractales, donde este parámetro es un valor fraccionario. La dimensión fractal de las matemáticas puede ser considerado convencionalmente como "desigual." Cuanto mayor sea la curva de rugosidad, mayor es su dimensión fractal. La curva tiene al Mandelbrot dimensión fractal mayor que su dimensión topológica, tiene una longitud aproximada de las cuales no depende del número de mediciones.
Ahora los científicos están descubriendo más y más áreas de aplicar la teoría de los fractales.
Conclusión
y
Fuente:























