Отображение сил гравитации Солнечной системы

Предисловие

Зачастую очень сложно объяснить словами самые простые вещи или устройство того или иного механизма. Но обычно, понимание приходит достаточно легко, если увидеть их глазами, а еще лучше и покрутить в руках. Но некоторые вещи невидимы для нашего зрения и даже будучи простыми очень сложны для понимания.
Например, что такое электрический ток — есть множество определений, но ни одно из них не описывает его механизм в точности, без двусмысленности и неопределенности.
С другой стороны, электротехника достаточно сильно развитая наука, в которой с помощью математических формул подробно описываются любые электрические процессы.
Так вот почему бы не показать подобные процессы с помощью этих самых формул и компьютерной графики.
Но сегодня рассмотрим действие более простого процесса, чем электричество — силу тяготения. Казалось бы, что там сложного, ведь закон всемирного тяготения изучают в школе, но тем не менее… Математика описывает процесс так, как он проходит в идеальных условиях, в некоем виртуальном пространстве, где нет никаких ограничений.
В жизни обычно все не так и на рассматриваемый процесс непрерывно накладывается множество различных обстоятельств, незаметных или несущественных на первый взгляд.
Знать формулу и понимать её действие — это немножко разные вещи.
Итак, сделаем небольшой шаг к пониманию закона тяготения. Сам закон прост — сила тяготения прямо пропорциональна массам и обратно пропорциональна квадрату расстояния между ними, но сложность заключается в невообразимом количестве взаимодействующих объектов.
Да, будем рассматривать только силу тяготения, так сказать, в полном одиночестве, что конечно неверно, но в данном случае допустимо, так как это просто способ показать невидимое.
И еще, в статье есть код JavaScript, т.е. все рисунки на самом деле нарисованы с помощью Canvas, поэтому целиком статью можно взять здесь.

Отображение возможностей гравитации в Солнечной системе

В рамках классической механики гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения F между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием r, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть:



где G — гравитационная постоянная, равная примерно 6,67384×10^-11 Н×м²×кг^-2.
Но мне бы хотелось бы видеть картинку изменения силы тяготения по всей солнечной системе, а не между двумя телами. Поэтому массу второго тела m₂ возьмем равной 1, а массу первого тела обозначим просто m. (То есть, представляем объекты в виде материальной точки — размером в один пиксел, а силу притяжения измеряем относительно другого, виртуального объекта, назовем его «пробным телом», с массой 1 килограмм.) При этом формула будет иметь вид:



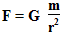
Теперь, вместо m подставляем массу интересующего тела, а вместо r перебираем все расстояния от 0 до значения орбиты последней планеты и получим изменение силы тяготения в зависимости от расстояния.
При наложении сил от разных объектов выбираем большую по величине.
Далее, выражаем эту силу не в цифрах, а в соответствующим им оттенках цвета. При этом получится наглядная картинка распределения гравитации в солнечной системе. То есть в физическом смысле, оттенок цвета будет соответствовать весу тела массой 1 килограмм в соответствующей точке солнечной системы.
Следует заметить, что:

• сила тяготения всегда положительна, не имеет отрицательных значений, т.е. масса не может быть отрицательной
• сила тяготения не может быть равна нулю, т.е. объект либо существует с какой-то массой, либо не существует вообще
• силу тяготения нельзя ни заэкранировать, ни отразить (как луч света зеркалом).

(собственно, вот и все ограничения, налагаемые физикой на математику в данном вопросе).
Давайте теперь рассмотрим как отобразить величины силы тяготения цветом.

Чтобы показать числа цветом нужно создать массив в котором индекс был бы равен числу, а значением являлось значение цвета в системе RGB.
Вот градиент цвета от белого к красному, затем желтому, зеленому, синему, фиолетовому и черному. Всего получилось 1786 оттенков цвета.


Количество цветов не так уж и велико, их просто не хватит для отображения всего спектра сил тяготения. Ограничимся силами тяготения от максимальной — на поверхности Солнца и минимальной — на орбите Сатурна. То есть, если силу притяжения на поверхности Солнца (270,0 Н) обозначить цветом, находящимся в таблице под индексом 1, то сила притяжения к Солнцу на орбите Сатурна (0,00006 Н) будет обозначена цветом, с индексом далеко за 1700. Так что все равно цветов не хватит для равномерного выражения величин силы тяготения.
Для того чтобы было хорошо видно самые интересные места в отображаемых силах притяжения нужно чтобы величинам силы притяжения меньше 1Н соответствовали большие изменения цвета, а от 1Н и выше, соответствия не так интересны — видно что сила притяжения, скажем Земли, отличается от притяжения Марса или Юпитера, да и ладно. То есть, цвет не будет пропорционален величине силы притяжения, иначе мы «потеряем» самое интересное.
Для приведения значения силы притяжения к индексу таблицы цвета воспользуемся следующей формулой:



Да, это та самая гипербола, известная ещё со средней школы, только предварительно из аргумента извлечен квадратный корень. (Взято чисто «от фонаря», только для того, чтобы уменьшить соотношение между самым большим и самым маленьким значениями силы притяжения.)
Посмотрите как распределятся цвета в зависимости от притяжения Солнца и планет.


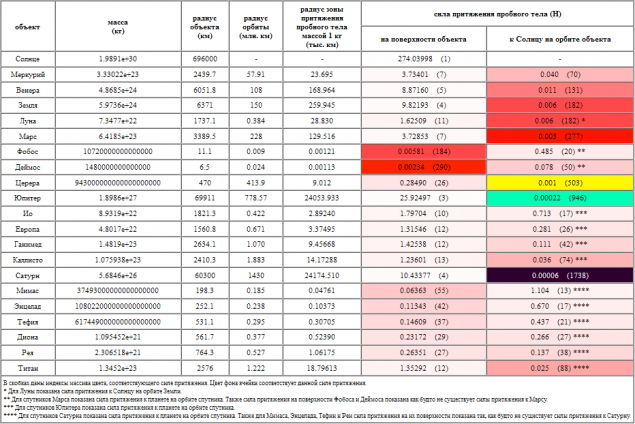
Как видите на поверхности Солнца наше пробное тело будет весить около 274Н или 27,4 кГс, так как 1 Н = 0,10197162 кгс = 0,1 кгс. А на Юпитере почти 26Н или 2,6 кгс, на Земле наше пробное тело весит около 9,8Н или 0,98кгс.
В принципе, все эти цифры очень-очень приблизительные. Для нашего случая это не очень важно, нам нужно превратить все эти значения силы притяжения в соответствующие им значения цвета.
Итак, из таблицы видно, что максимальная величина силы притяжения равна 274Н, а минимальная 0,00006Н. То есть разнятся более чем в 4,5 миллиона раз.

Также видно что все планеты получились почти одного цвета. Но это неважно, важно что будет хорошо видно границы притяжения планет, так как силы притяжения малых значений достаточно хорошо изменяются по цвету.
Конечно, точность невелика, но нам и нужно просто получить общее представление о силах гравитации в Солнечной системе.
Теперь «расставим» планеты в места, соответствующие их удалению от Солнца. Для этого к полученному градиенту цвета нужно приделать какое-то подобие шкалы расстояний. Кривизну орбит, я думаю, можно не учитывать.
Но как всегда космические масштабы, в прямом смысле этих слов, не дают увидеть картинку целиком. Смотрим, Сатурн находится приблизительно в 1430 миллионах километров от Солнца, индекс соответствующий цвету его орбиты равен 1738. Т.е. получается в одном пикселе (если брать в этом масштабе один оттенок цвета равен одному пикселу) приблизительно 822,8 тысяч километров. А радиус Земли приблизительно 6371 километр, т.е. диаметр 12742 километра, где-то в 65 раз меньше одного пиксела. Вот и как тут соблюдать пропорции.
Мы пойдем другим путем.© Так как нам интересна гравитация околопланетного пространства, то будем брать планеты по отдельности и раскрашивать их и пространство вокруг них цветом, соответствующим гравитационным силам от них самих и Солнца. Например, возьмем Меркурий — радиус планеты 2,4 тыс. км. и приравняем его к кругу диаметром 48 пикселов, т.е. в одном пикселе будет 100 км. Тогда Венера и Земля будут соответственно 121 и 127 пикселов. Вполне удобные размеры.
Итак, делаем картинку размером 600 на 600 пикселов, определяем значение силы притяжения к Солнцу на орбите Меркурия плюс/минус 30000 км (чтобы планета получилась в центре картинки) и закрашиваем фон градиентом оттенков цвета соответствующим этим силам.
При этом, для упрощения задачи, закрашиваем не дугами, соответствующего радиуса, а прямыми, вертикальными линиями. (Грубо говоря, наше «Солнце» будет «квадратным» и всегда будет находиться на левой стороне.)
Для того, чтобы цвет фона не просвечивался сквозь изображение планеты и зоны притяжения к планете, определяем радиус окружности, соответствующей зоне, где притяжение к планете больше притяжения к Солнцу и закрашиваем её в белый цвет.
Затем в центр картинки помещаем круг, соответствующий диаметру Меркурия в масштабе (48 пикселов) и заливаем его цветом, соответствующим силе притяжения к планете на её поверхности.
Далее от планеты закрашиваем градиентом в соответствии с изменением силы притяжения к ней и при этом постоянно сравниваем цвет каждой точки в слое притяжения к Меркурию с точкой с такими же координатами, но в слое притяжения к Солнцу. Когда эти значения становятся равными, делаем этот пиксел черным и дальнейшее закрашивание прекращаем.
Таким образом получим некую форму видимого изменения силы притяжения планеты и Солнца с четкой границей между ними черного цвета.
(Хотелось сделать именно так, но… не получилось, не смог сделать попиксельное сравнение двух слоев изображения.)

По расстоянию 600 пикселов равны 60 тыс. километров (т.е. один пиксел — 100 км).
Сила притяжения к Солнцу на орбите Меркурия и возле него изменяется лишь в небольшом диапазоне, который в нашем случае обозначается одним оттенком цвета.


Итак, Меркурий и сила тяготения в окрестностях планеты.
Сразу следует отметить, что восемь малозаметных лучей это дефекты от рисования окружностей в Canvas. Они не имеют никакого отношения к обсуждаемому вопросу и их следует просто не замечать.
Размеры квадрата 600 на 600 пикселей, т.е. это пространство в 60 тыс. километров. Радиус Меркурия 24 пиксела — 2,4 тыс. км. Радиус зоны притяжения 23,7 тыс. км.
Круг в центре, который почти белого цвета, это сама планета и её цвет соответствует весу нашего килограммового пробного тела на поверхности планеты — около 373 грамм. Тонкая окружность синего цвета показывает границу между поверхностью планеты и зоной, в которой сила тяготения к планете превышает силу тяготения к Солнцу.
Далее цвет постепенно изменяется, становится все более красным (т.е. вес пробного тела уменьшается) и наконец, становится равным цвету, соответствующему силе притяжения к Солнцу в данном месте, т.е. на орбите Меркурия. Граница между зоной где сила притяжения к планете превышает силу притяжения к Солнцу также отмечена синей окружностью.
Как видите, ничего сверхъестественного нет.
Но в жизни несколько другая картина. Например, на этом и всех остальных изображениях, Солнце находится слева, значит на самом деле, область притяжения планеты должна быть немного «сплющена» слева и вытянута справа. А на изображении — окружность.
Конечно, лучшим вариантом было бы попиксельное сравнение области притяжения к Солнцу и области притяжения к планете и выбор (отображение) большей из них. Но на такие подвиги ни я, как автор этой статьи, ни JavaScript не способны. Работа с многомерными массивами не является приоритетной для данного языка, зато его работу можно показать практически в любом браузере, что и решило вопрос применения.
Да и в случае Меркурия, и всех остальных планет земной группы, изменение силы притяжения к Солнцу не так велико, чтобы отобразить его имеющимся набором оттенков цвета. А вот при рассмотрении Юпитера и Сатурна изменение силы притяжения к Солнцу очень даже заметно.

Венера

Собственно, все тоже самое что и у предыдущей планеты, только размер Венеры и её масса значительно больше, а сила притяжения к Солнцу на орбите планеты меньше (цвет более темный, вернее, более красный), а планета большей массы, поэтому цвет диска планеты более светлый.
Для того чтобы на рисунке 600 на 600 пикселов поместилась планета с зоной притяжения пробного тела массой 1 кг уменьшим масштаб в 10 раз. Теперь в одном пикселе 1 тысяча километров.

Земля+Луна

Чтобы показать Землю и Луну изменить масштаб в 10 раз (как в случае с Венерой) недостаточно, нужно увеличить и размер картинки (радиус орбиты Луны 384,467 тыс. км). Картинка получится размером 800 на 800 пикселей. Масштаб — в одном пикселе 1 тысяча километров (хорошо понимаем что ошибочность картинки ещё больше увеличится).


На картинке четко видно что зоны притяжения Луны и Земли разделены зоной притяжения к Солнцу. То есть, Земля и Луна это система из двух равнозначных планет с разной массой.

Марс с Фобосом и Деймосом

Масштаб — в одном пикселе 1 тысяча километров. Т.е. как Венера, и Земля с Луной. Помним, что расстояния пропорциональны, а отображение силы тяжести нелинейно.


Вот, сразу видно коренное отличие Марса со спутниками от Земли с Луной. Если Земля и Луна являются системой двух планет и, несмотря на разные размеры и массы, выступают как равные партнеры, то спутники Марса находятся в зоне силы притяжения Марса.
Сама планета и спутники практически «потерялись». Белая окружность это орбита дальнего спутника — Деймоса. Увеличим в 10 раз масштаб для лучшего просмотра. В одном пикселе 100 километров.


Эти «жуткие» лучи от Canvas достаточно сильно портят картинку.
Размеры Фобоса и Деймоса непропорционально увеличены в 50 раз, иначе их совсем не видно. Цвет поверхностей этих спутников также не логичен. На самом деле сила притяжения на поверхностях этих планетах меньше силы притяжения к Марсу на их орбитах.
То есть, с поверхностей Фобоса и Деймоса притяжением Марса «сдувает» все. Поэтому цвет их поверхностей должен быть равен цвету на их орбитах, но только для того чтобы было лучше видно, диски спутников окрашены в цвет силы притяжения при отсутствии силы притяжения к Марсу.
Эти спутники должны быть просто монолитны. Кроме того, раз уж на поверхности нет силы притяжения, значит они не могли сформироваться в таком виде, то есть и Фобос и Деймос раньше были частями какого-то другого, большего объекта. Ну или, как минимум, находились в другом месте, с меньшей силой притяжения, чем в зоне притяжения Марса.
Например, вот Фобос. Масштаб — в одном пикселе 100 метров.
Поверхность спутника обозначена синей окружностью, а сила притяжения всей массы спутника белой окружностью.
(На самом деле форма небольших небесных тел Фобоса, Деймоса и т.д. далеко не шарообразна)
Цвет кружка в центре соответствует силе притяжения массы спутника. Чем ближе к поверхности планеты, тем меньше сила притяжения.
(Здесь опять допущена неточность. На самом деле белая окружность — это граница, где сила притяжения к планете становится равной силе притяжения к Марсу на орбите Фобоса.
То есть, цвет снаружи от этой белой окружности должен быть таким же как и снаружи от синей окружности, обозначающей поверхность спутника. А вот показанный переход цвета должен быть внутри белой окружности. Но тогда вообще ничего не будет видно.)
Получается как бы рисунок планеты в разрезе.
Целостность планеты определяется только прочностью материала, из которого состоит Фобос. При меньшей прочности у Марса были бы кольца как у Сатурна, от разрушения спутников.


Да и похоже, что распад космических объектов не такое уж исключительное событие. Вот даже космический телескоп «Хаббл» «засёк» подобный случай.

Распад астероида P/2013 R3
Распад астероида P/2013 R3

Распад астероида P/2013 R3, который находится на расстоянии более 480 миллионов километров от Солнца (в поясе астероидов, дальше Цереры). Диаметр четырех крупнейших фрагментов астероида достигает 200 метров, их общая масса составляет около 200 тысяч тонн.
А это Деймос. Все тоже, что и у Фобоса. Масштаб — в одном пикселе 100 метров. Только планета поменьше и соответственно полегче, а также находится дальше от Марса и сила притяжения к Марсу здесь поменьше (фон картинки потемнее, т.е. более красный).


Церера
Ну Церера ничего особенного не представляет, за исключением раскраски. Сила притяжения к Солнцу здесь меньше, поэтому цвет соответствующий. Масштаб — в одном пикселе 100 километров (такой же как на картинке с Меркурием).
Маленькая синяя окружность это поверхность Цереры, а большая синяя — граница, где сила притяжения к планете становится равной силе притяжения к Солнцу.

Юпитер

Юпитер очень велик. Вот картинка размером 800 на 800 пикселей. Масштаб — в одном пикселе 100 тысяч километров. Это чтобы показать область притяжения планеты целиком. Сама планета — маленькая точка в центре. Спутники не показаны.
Показана только орбита (внешняя окружность белого цвета) самого дальнего спутника — S/2003 J 2.


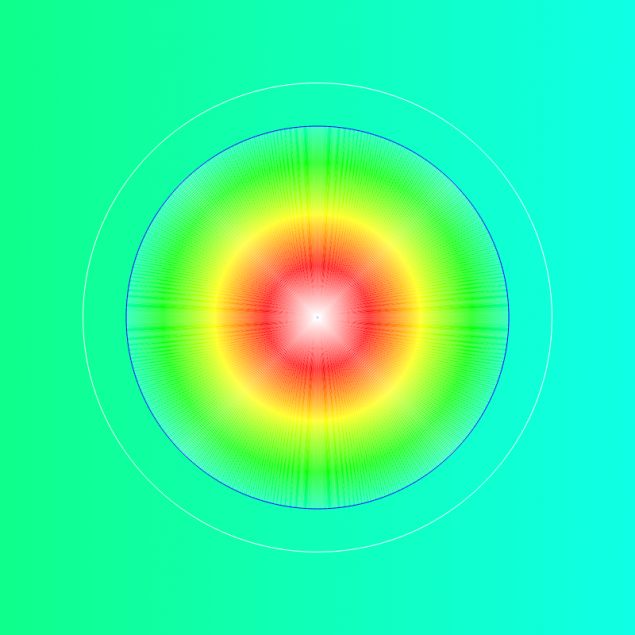
У Юпитера 67 спутников. Самые крупные Ио, Европа, Ганимед и Каллисто.
Самый дальний спутник — S/2003 J 2 совершает полный оборот вокруг Юпитера на расстоянии в среднем 29 541 000 км. Его диаметр около 2 км, масса — около 1,5×10¹³ кг. Как видите, она выходит далеко за пределы сферы тяготения планеты. Это можно объяснить ошибками в вычислениях (все-таки сделано довольно много усреднений, округлений и отбрасывания некоторых деталей).
Хотя имеется способ вычисления границы гравитационного влияния Юпитера, определямый сферой Хилла, радиус которой определяется формулой



где a_jupiter и m_jupiter большая полуось эллипса и масса Юпитера, а M_sun масса Солнца. Таким образом получается радиус округлённо 52 миллиона км. S/2003 J 2 отдаляется на эксцентрической орбите на расстояние до 36 миллионов км от Юпитера
У Юпитера также имеется система колец из 4 основных компонентов: толстый внутренний тор из частиц, известный как «кольцо-гало»; относительно яркое и тонкое «Главное кольцо»; и два широких и слабых внешних кольца — известных как «паутинные кольца», называющиеся по материалу спутников — которые их и формируют: Амальтеи и Фивы.
Кольцо-гало с внутренним радиусом 92000 и внешним 122500 километров.
Главное кольцо 122500—129000 км.
Паутинное кольцо Амальтеи 129000—182000км.
Паутинное кольцо Фивы 129000—226000 км.
Увеличим картинку в 200 раз, в одном пикселе 500 километров.
Вот кольца Юпитера. Тонкая окружность — поверхность планеты. Далее идут границы колец — внутренняя граница кольца-гало, внешняя граница кольца-гало и она же внутренняя граница главного кольца и т.д.
Маленький кружок в левом верхнем углу — область, где сила притяжения спутника Юпитера Ио становится равной силе притяжения Юпитера на орбите Ио. Сам спутник в этом масштабе просто не виден.


В принципе, большие планеты со спутниками нужно рассматривать отдельно, так как перепад значений сил гравитации очень велик, как велики и размеры области притяжения планеты. Вследствие этого все интересные подробности просто теряются. А рассматривать картинку с радиальным градиентом не имеет особого смысла.

Сатурн

Картинка размером 800 на 800 пикселей. Масштаб — в одном пикселе 100 тысяч километров. Сама планета — маленькая точка в центре. Спутники не показаны.
Четко видно изменение силы притяжения к Солнцу (помним что Солнце слева).


У Сатурна известно 62 спутника. Крупнейшие из них — Мимас, Энцелад, Тефия, Диона, Рея, Титан и Япет.
Самый дальний спутник — Форньот (временное обозначение S/2004 S 8). Также обозначается как Сатурн XLII. Средний радиус спутника около 3 километров, масса 2,6×10¹⁴ кг, большая полуось 25146000 км.
Кольца у планет появляются только на значительном удалении от Солнца. Первая такая планета — Юпитер. Имея массу и размеры большие чем у Сатурна, его кольца не так впечатляют как кольца Сатурна. То есть, размеры и масса планеты для образования колец имеют меньшее значение, чем отдаленность от Солнца.
Зато смотрите дальше, пара колец окружает астероид Харикло (10199 Chariklo) (диаметр астероида около 250 километров), который вращается вокруг Солнца между Сатурном и Ураном.
Статья на Хабре о астероиде с кольцами
Википедия о астероиде Харикло
Система колец состоит из плотного внутреннего кольца шириной в 7 км и внешнего кольца шириной в 3 км. Расстояние между кольцами около 9 км. Радиусы колец 396 и 405 км соответственно. Харикло является наименьшим объектом, у которого были открыты кольца.
Тем не менее, сила тяготения имеет к кольцам только опосредованное отношение.
На самом деле, кольца появляются от разрушения спутников, которые состоят из материала недостаточной прочности, т.е. не каменные монолиты типа Фобоса или Деймоса, а смерзшиеся в одно целое куски породы, льда, пыль и прочий космический мусор.
Вот его и утаскивает своим тяготением планета. Подобный спутник, не имеющий собственного притяжения (вернее имеющий силу собственного притяжения меньше силы притяжения к планете на своей орбите) летит по орбите оставляя после себя шлейф разрушенного материала. Так и образуется кольцо. Далее, под действием силы притяжения к планете, этот обломочный материал приближается к планете. То есть, кольцо расширяется.
На каком-то уровне, сила притяжения становится достаточно большой, чтобы скорость падения этих обломков увеличилась, и кольцо исчезает.

Послесловие

Цель публикации статьи — возможно кто-то, обладающий знаниями в программировании, заинтересуется данной темой и сделает более качественную модель гравитационных сил в Солнечной системе (да-да, трехмерную, с анимацией.
А может быть даже сделает так, чтобы орбиты были не фиксированы, а также рассчитывались — это ведь тоже возможно, орбита будет местом, где сила притяжения будет компенсирована центробежной силой.
Получится почти как в жизни, как самая настоящая Солнечная система. (Вот где можно будет создать космическую стрелялку, со всеми тонкостями космической навигации в поясе астероидов. С учетом сил, действующих по реальным физическим законам, а не среди рисованной графики.)
И это будет прекрасный учебник физики, которую будет интересно изучать.
P.S. Автор статьи обычный человек:
не физик,
не астроном,
не программист,
не имеет высшего образования.

Источник: habrahabr.ru/post/227127/