1217
Симетрія природи
Протягом століть симетрія залишалася суб'єктом, що зачаровує філософів, астрономів, математиків, митців, архітекторів та фізико-психологів. Стародавні греки були ерозійними з ним – і навіть сьогодні ми прагнемо зіткнутися з симетрією в усьому від планування наших меблів для різання нашого волосся.

Брокколі Романеско
Ви можете побачити романш broccoli в магазині і подумати, що це був ще один зразок генетично модифікованого продукту. Але це насправді ще один приклад фрактальної симетрії в природі. Кожен броколі суцвіття має логарифмічний спіральний візерунок. Романеско схожий на брокколі, а за смаком і консистенцією – цвітну. Це багатий каротиноїдами, а також вітамінами С і К, що робить його не тільки красивими, але і здоровими продуктами.

медуми
На тисячу років люди одружилися в ідеальному шестигранній формі медиків і просять себе, як бджіл може інстинктивно створити форму, яка людина може тільки відтворювати з компасом і лінійкою. Як і чому бджоли мають пристрасть до створення шестикутників? Математологи вважають, що це ідеальна форма, яка дозволяє зберігати якомога більше меду. У будь-якому випадку, це весь продукт природи, і це дратує ефект.

соняшники
Соняшники можуть похвалитися радіальною симетрією і цікавим типом симетрії, відомого як послідовність Fibonacci. Фібоначчі послідовність: 1, 2, 3, 5, 8, 13, 21, 24, 55, 89, 144 і т.д. (у вартість визначається сумою двох попередніх чисел). Якщо ми взяли наш час і підрахували кількість насіння в соняшнику, ми знайдемо, що кількість спіралей збільшується за принципами послідовності Фобнаци. Є так багато рослин в природі (в тому числі романсco broccoli) пелюстки, насіння і листя відповідають цій послідовності, тому важко знайти чотирилистовий конюшина.
Але чому соняшники та інші рослини дотримуються математичних правил? Як і гексагони в животі, це все питання ефективності.

Nautilus мийка
Крім рослин, деякі тварини, такі як Nautilus, відповідають послідовності Fibonacci. Оболонка Nautilus перекручує в «Фібоначські спіралі». Оболонка намагається підтримувати однакову пропорційну форму, яка дозволяє підтримувати її протягом усього життя (не схожих людей, які змінюють пропорції протягом усього життя). Не всі Nautilus мають оболонку Fibonacci, але всі вони слідують логарифмічної спіралі.
До того, як ви заздрили магтематики, пам'ятайте, що вони не роблять це з метою того, щоб ця форма була найбільш раціональна для них.
 доб.1
доб.1
Тварини
Більшість тварин мають двосторонню симетрію, що означає, що їх можна розділити на дві ідентичні половинки. Навіть люди мають двосторонню симетрію, і деякі вчені вважають, що людська симетрія є найважливішим фактором, який впливає на наше сприйняття краси. Іншими словами, якщо у вас є одностороння особа, то сподіваємось, що вона буде компенсувати інші хороші якості.
Деякі досягають точки повної симетрії у зусиллях залучення партнера, таких як півень. Дарвін був позитивно занурений птахом, і написав у листі, що «Примітка перо в хвостику півень, коли я виглядав на ньому, змушує мене хворі!» До Дарвіна, хвіст зданий тягарним і без еволюційного значення, так як він не вписав його теорію "сюрваль відповідника". Він був лютий до тих пір, поки він прийшов з теорію сексуального вибору, що говорить про те, що тварини розвивають певні функції, щоб збільшити свої шанси дозрівання. Таким чином, паяки мають різні пристрої для залучення партнера.

Веб-сайт
Існує близько 5,000 видів павуків, і всі вони створюють ближній круговий полотно з радіальними підтримуючими нитками на майже рівній відстані і спіральній тканині для зловлювання преси. Вчені не впевнені, що павуки люблять геометрію так багато, оскільки тести показали, що кругле полотно не буде виглядати краще, ніж нерегулярно сформоване полотно. Вчені свідчать про те, що радіальна симетрія рівномірно розподіляє силу впливу, коли потерпілий надходить в мережу, в результаті чого менше зазорів.
 р.
р.
Крупні кола
Подаруйте пару обманів дошки, косарки, і живу темряву, і ви побачите, що людина створює симетричні форми. У зв’язку з тим, що культурні кола відрізнялися складністю дизайну і неймовірною симетрією, навіть після творців кола зізналися і продемонстрували свою майстерність, багато людей все одно вірять, що космічні відчуження робили це.
Як стають більш складними, їх штучне походження стає більш чітким. Ілологічно припустити, що іноземці зроблять їх повідомлення більш складними, коли ми не змогли розшифрувати навіть перші.
Незалежно від того, як вони прийшли до того, що зернові кола приємно бачити, в основному, тому що їх геометрія вражає.
 Р
Р
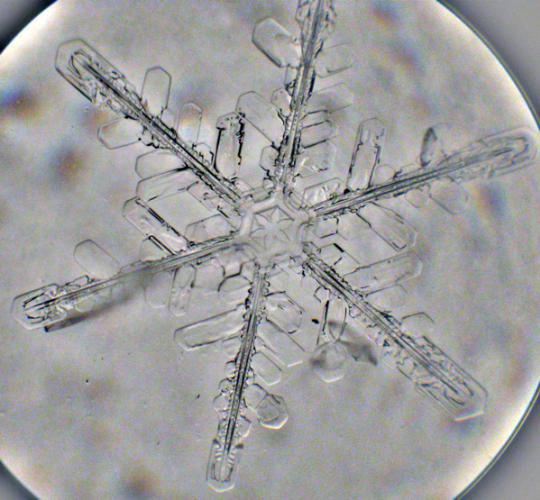
Сніжинки
Навіть крихітні утворення, такі як сніжинки регулюються законами симетрії, оскільки більшість сніжинок мають шестикутну симетрію. Це пов'язано з тим, що молекули води підкреслюють, коли тверді (кристалізуються). молекули води набувають твердого стану, утворюючи слабкі водні зв'язки, вони вирівнюються в замовленій обстановці, що балансує сили тяжіння і відбиття, утворюючи шестигранну форму сніжинки. Кожна сніжинка симетрична, але не сніжинка схожа на інший. Це тому, що кожна сніжинка потрапляє з неба і відчуває унікальні атмосферні умови, які викликають кристали, щоб вирівняти певним чином.
The Milky Way Галактика
Як ми бачили, симетрія і математичні моделі існують практично скрізь, але ці закони природи, що суперечать нашій планеті? Зрозуміло, Нещодавно відкрився новий розділ на краю галактики «Молочний шлях», а астрономи вважають, що галактика є майже ідеальним дзеркальним зображенням себе.
139992р.
Сонце-мона симетрія
З огляду на те, що Сонячний має діаметр 1,4 млн км і Місяць становить 3,474 км, здається практично неможливим, що Місяця може блокувати сонячні промені і забезпечити нам близько п'яти сонячних затисків кожні два роки. Як це працює? Coincidentally, в той час як Сонце близько 400 разів, як широкий Місяця, Сонце також 400 разів як далеко. Симметрія забезпечує, що Сонце і Місяць є однаковим розміром при перегляді з Землі, тому Місяць може покрити Сонце. Звичайно, відстань від Землі до Сонця може збільшитися, тому іноді ми бачимо кутові і неповні застібки. Але кожен до двох років є чітким вирівнюванням, і ми свідками вражаючих подій, відомих як загальний сонячний ексліпс. Астрономи не знають, як часто ця симетрія є серед інших планет, але вони думають, що це рідкісне явище. Але не варто припустити, що ми є особливим, оскільки все це питання шансу. Наприклад, кожен рік Місяць переходить близько 4 см від Землі, що означає, що мільярди років тому кожен сонячний екліпс був загальним екліпсом. Якщо все йде на так, то зникнуть загальні застібки, і це буде супроводжуватися зникненням кутових застібок. Ми в правильному місці, щоб побачити це явище.

Джерело: bigpicture.ru

Брокколі Романеско
Ви можете побачити романш broccoli в магазині і подумати, що це був ще один зразок генетично модифікованого продукту. Але це насправді ще один приклад фрактальної симетрії в природі. Кожен броколі суцвіття має логарифмічний спіральний візерунок. Романеско схожий на брокколі, а за смаком і консистенцією – цвітну. Це багатий каротиноїдами, а також вітамінами С і К, що робить його не тільки красивими, але і здоровими продуктами.

медуми
На тисячу років люди одружилися в ідеальному шестигранній формі медиків і просять себе, як бджіл може інстинктивно створити форму, яка людина може тільки відтворювати з компасом і лінійкою. Як і чому бджоли мають пристрасть до створення шестикутників? Математологи вважають, що це ідеальна форма, яка дозволяє зберігати якомога більше меду. У будь-якому випадку, це весь продукт природи, і це дратує ефект.

соняшники
Соняшники можуть похвалитися радіальною симетрією і цікавим типом симетрії, відомого як послідовність Fibonacci. Фібоначчі послідовність: 1, 2, 3, 5, 8, 13, 21, 24, 55, 89, 144 і т.д. (у вартість визначається сумою двох попередніх чисел). Якщо ми взяли наш час і підрахували кількість насіння в соняшнику, ми знайдемо, що кількість спіралей збільшується за принципами послідовності Фобнаци. Є так багато рослин в природі (в тому числі романсco broccoli) пелюстки, насіння і листя відповідають цій послідовності, тому важко знайти чотирилистовий конюшина.
Але чому соняшники та інші рослини дотримуються математичних правил? Як і гексагони в животі, це все питання ефективності.

Nautilus мийка
Крім рослин, деякі тварини, такі як Nautilus, відповідають послідовності Fibonacci. Оболонка Nautilus перекручує в «Фібоначські спіралі». Оболонка намагається підтримувати однакову пропорційну форму, яка дозволяє підтримувати її протягом усього життя (не схожих людей, які змінюють пропорції протягом усього життя). Не всі Nautilus мають оболонку Fibonacci, але всі вони слідують логарифмічної спіралі.
До того, як ви заздрили магтематики, пам'ятайте, що вони не роблять це з метою того, щоб ця форма була найбільш раціональна для них.
 доб.1
доб.1Тварини
Більшість тварин мають двосторонню симетрію, що означає, що їх можна розділити на дві ідентичні половинки. Навіть люди мають двосторонню симетрію, і деякі вчені вважають, що людська симетрія є найважливішим фактором, який впливає на наше сприйняття краси. Іншими словами, якщо у вас є одностороння особа, то сподіваємось, що вона буде компенсувати інші хороші якості.
Деякі досягають точки повної симетрії у зусиллях залучення партнера, таких як півень. Дарвін був позитивно занурений птахом, і написав у листі, що «Примітка перо в хвостику півень, коли я виглядав на ньому, змушує мене хворі!» До Дарвіна, хвіст зданий тягарним і без еволюційного значення, так як він не вписав його теорію "сюрваль відповідника". Він був лютий до тих пір, поки він прийшов з теорію сексуального вибору, що говорить про те, що тварини розвивають певні функції, щоб збільшити свої шанси дозрівання. Таким чином, паяки мають різні пристрої для залучення партнера.

Веб-сайт
Існує близько 5,000 видів павуків, і всі вони створюють ближній круговий полотно з радіальними підтримуючими нитками на майже рівній відстані і спіральній тканині для зловлювання преси. Вчені не впевнені, що павуки люблять геометрію так багато, оскільки тести показали, що кругле полотно не буде виглядати краще, ніж нерегулярно сформоване полотно. Вчені свідчать про те, що радіальна симетрія рівномірно розподіляє силу впливу, коли потерпілий надходить в мережу, в результаті чого менше зазорів.
 р.
р.Крупні кола
Подаруйте пару обманів дошки, косарки, і живу темряву, і ви побачите, що людина створює симетричні форми. У зв’язку з тим, що культурні кола відрізнялися складністю дизайну і неймовірною симетрією, навіть після творців кола зізналися і продемонстрували свою майстерність, багато людей все одно вірять, що космічні відчуження робили це.
Як стають більш складними, їх штучне походження стає більш чітким. Ілологічно припустити, що іноземці зроблять їх повідомлення більш складними, коли ми не змогли розшифрувати навіть перші.
Незалежно від того, як вони прийшли до того, що зернові кола приємно бачити, в основному, тому що їх геометрія вражає.
 Р
РСніжинки
Навіть крихітні утворення, такі як сніжинки регулюються законами симетрії, оскільки більшість сніжинок мають шестикутну симетрію. Це пов'язано з тим, що молекули води підкреслюють, коли тверді (кристалізуються). молекули води набувають твердого стану, утворюючи слабкі водні зв'язки, вони вирівнюються в замовленій обстановці, що балансує сили тяжіння і відбиття, утворюючи шестигранну форму сніжинки. Кожна сніжинка симетрична, але не сніжинка схожа на інший. Це тому, що кожна сніжинка потрапляє з неба і відчуває унікальні атмосферні умови, які викликають кристали, щоб вирівняти певним чином.

The Milky Way Галактика
Як ми бачили, симетрія і математичні моделі існують практично скрізь, але ці закони природи, що суперечать нашій планеті? Зрозуміло, Нещодавно відкрився новий розділ на краю галактики «Молочний шлях», а астрономи вважають, що галактика є майже ідеальним дзеркальним зображенням себе.
139992р.
Сонце-мона симетрія
З огляду на те, що Сонячний має діаметр 1,4 млн км і Місяць становить 3,474 км, здається практично неможливим, що Місяця може блокувати сонячні промені і забезпечити нам близько п'яти сонячних затисків кожні два роки. Як це працює? Coincidentally, в той час як Сонце близько 400 разів, як широкий Місяця, Сонце також 400 разів як далеко. Симметрія забезпечує, що Сонце і Місяць є однаковим розміром при перегляді з Землі, тому Місяць може покрити Сонце. Звичайно, відстань від Землі до Сонця може збільшитися, тому іноді ми бачимо кутові і неповні застібки. Але кожен до двох років є чітким вирівнюванням, і ми свідками вражаючих подій, відомих як загальний сонячний ексліпс. Астрономи не знають, як часто ця симетрія є серед інших планет, але вони думають, що це рідкісне явище. Але не варто припустити, що ми є особливим, оскільки все це питання шансу. Наприклад, кожен рік Місяць переходить близько 4 см від Землі, що означає, що мільярди років тому кожен сонячний екліпс був загальним екліпсом. Якщо все йде на так, то зникнуть загальні застібки, і це буде супроводжуватися зникненням кутових застібок. Ми в правильному місці, щоб побачити це явище.

Джерело: bigpicture.ru























