670
Як зробити непристойні шпалери: Історія заборонених симетрій
На перший погляд, винахідливі шпалери не складніші, ніж виконання завдань з дитячого садка. Дизайнери можуть вибрати будь-яке поєднання кольорів і форм для оригінального виробу, і просто пропагувати його в двох напрямках. Залежно від візерунка початкового шматочка і вибору напрямків може з'явитися додаткові симпети – наприклад, симетрія шостого порядку в першій картині або дзеркальної симетрії в другому. Обидва візерунки були створені математикою Френка Фаріс університету Каліфорнія Санта Клара.

На лівому зображенні шпалер з симетрією поздовжнього порядку навколо кожного з коричнево-зелених точок. На правому зображенні шпалер з дзеркальною симетрією відносно горизонтальних ліній, що проходять через кожен еліптичний елемент вітражного орнаменту.
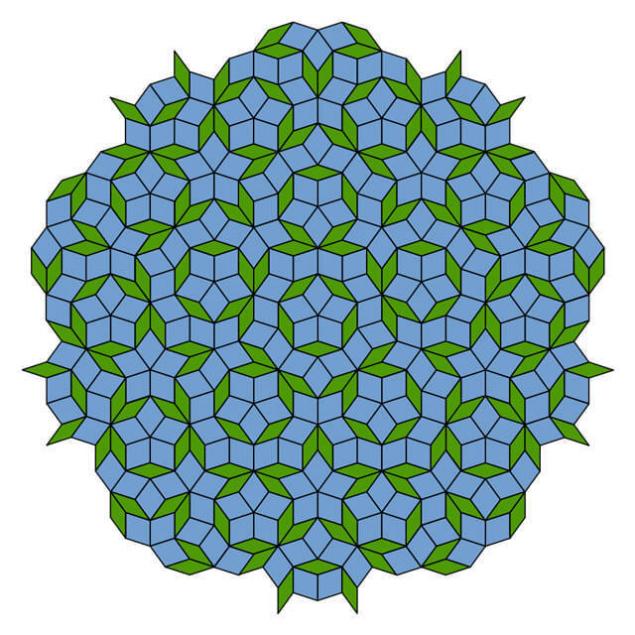
П'ятикутна плитка показує безліч прикладів симетрії місцевого п'ятого порядку, але вони не мають шаблонних повторень. При заповненні великих площ на площині, співвідношення кількості широких плиток до кількості вузьких підходів до золотого співвідношення.
Але, хоча можна зробити шпалери з обертальними symmetries другого, третього, четвертого або шостого порядку, неможливо створити шпалери з п'ятою симетрією замовлення (замовлення показує, скільки разів при обертанні 360 градусів візерунок буде самозніматися). Цей обмеження був відомий математикам протягом майже 200 років як кристалографічне обмеження. Геометрія петагона забороняє візерунки з симетрією п'ятого порядку. Так само, як і для замовлень сім або більше.
Тим не менш, найцікавіші візерунки, такі як кахель Penrose, експонують п'ятий порядок локальної симетрії в багатьох місцях і на різних масштабах, але без повторюваних візерунків. Використання методу відрізняється від підходу Penrose, Farris закриває незвичайну геометрію симетрії п'ятого порядку і створив новий набір захоплюючих образів – псевдо-паперовий, не піддається, на перший погляд, кристалографічні обмеження.
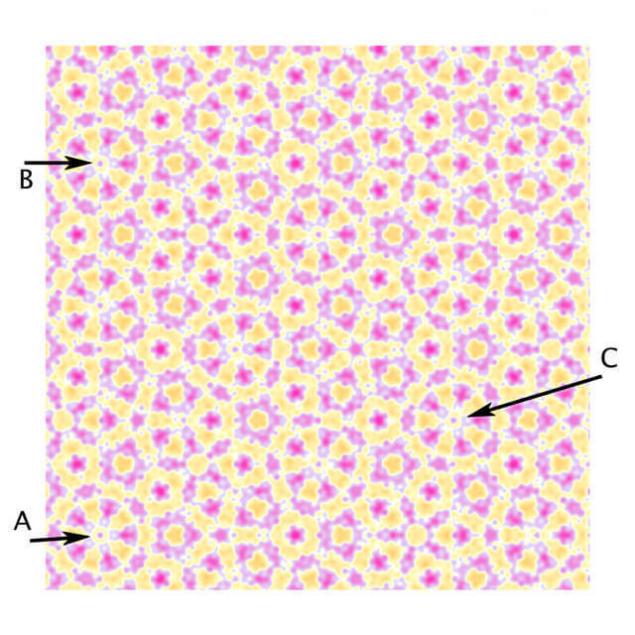
Рис. 4. У
Рисунок 4 схожий на контрабанду для кристалографічного обмеження, що має п'ятий порядок обертання симетрії навколо точки А, в той час як візерунок можна змінити на площині в напрямках AB або AC. По суті, Faris пише в своїй статті для журналу Повідомлень Американського Математичного товариства, що ця картина є просто розумною підробкою.
«Ви знаєте, що симетрія, яку ви не можете спостерігати, - говорить Стівен Кеннеді Карлтон Коледж в Міннесота.
П'ятий порядок обертання симетрії навколо точки Здається триматися. Але якщо ви подивитеся уважно, ви можете побачити, що колеса навколо B і C трохи відрізняються від A. Якщо ми змогли відійти від візерунка, щоб побачити більше повторень, очевидні повтори візерунка буде менше і менше, як візерунок навколо точки А, навіть якщо коли-небудь більш переконливі копії А були з'являтися в іншому місці, як на малюнку. 5. Faris показали, що такі ілюзії можуть бути створені на більших масштабах, відходячи від візерунка і повторюючи її певну кількість разів – зокрема, кількість разів, що відповідають номерам в серії Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, ... де кожен наступний номер є сумою попереднього двох), яка також грає роль в геометрії плитки Penrose.
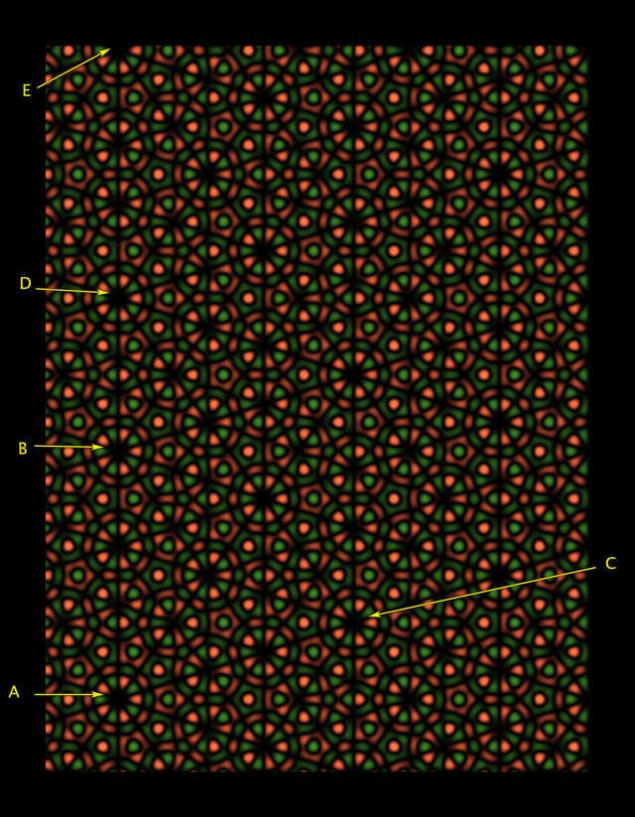
Рис. 5 хв
"Інтелектуальна практика змушує нас розуміти, що це таке децепція, - каже Faris. Я, як він пише в папці, ці зображення "насолодіться нашими думками, щоб вивчити їх і насолоджуватися відкритими повторами."
Faris прийшов з цими підробками, змінивши технологію, за допомогою якого він створив реальний 3-й порядок поворотних симетрій шпалер, таких як рис. 6. Жнівень
Для створення тримісної симетрії, Faris почав працювати в тривимірному просторі, що має одне особливо природне обертання, що проходить через три просторові координати, а поворотні точки в просторі 120 градусів навколо діагоналлю. Faris потім створюються об'ємні візерунки шпалер, які наділяються спеціально підібраними синусоїдами і поєднують їх з попередньо встановленою палітрою кольорів. Ознаки розфарбовувалися в залежності від їх положення на наділених синусоїдах. Потім Faris deduced плоскі шпалери, обмежуючи цей колір на двовимірну площину перпендикулярно осі обертання оригінального простору.
Цей плавний, синусоїдальний підхід до створення шпалерних візерунків відрізняється від традиційного способу копіювання і пасування, говорить Кеннеді. «Це дуже новий спосіб створення симетричних візерунків. й
 р.
р.
Рис. 6 хв
Так само процедура виконана в п'ятивимірному просторі, здається, виготовлялася з п'ятою симетрією замовлення. Я дивлюся, Faris дивився, в якому точка не виходить?
У теорії можливий п'ятивимірний простір, хоча складно уявити. Має природний аналог п'ятого порядку обертової симетрії, як і об'ємний простір – симетрія третього порядку. У п'ятивимірному просторі можна вибрати одну з двох площин, кожен перпендикулярно осі обертання і іншої площини. Кожен з них може бути обертається навколо точки 72 або 144 градусів. Здавалося б, важко уявити дві площини і пряму лінію перпендикулярно один одному, але в п'ять розмірах вони мають достатню кількість простору.
Faris розуміє проблему: якщо перпендикулярна площина акуратно розрізається через об'ємний простір, і містить нескінченні шпалери з нескінченною кількістю точок, що володіють цілими координатами, то дві перпендикулярні площини в п'ятивимірному просторі є irrational, і не містять точки з цілими координатами (крім точки посилання). Так як візерунок шпалер, створених з синусоїдів, повторюється через зсуви за цілими цілими, такі площини не впадуть у спадок візерунки в просторах вищого порядку.
«Так, як з'являється в супі,» Faris пише в статті.
Однак ілюзію структури шпалер з'являється на цих двох площинах, завдяки участі так званого золотого співвідношення, ірраціонального числа, що описує напрямки двох площин, і цифри Фібоначчі.
Цікаво: Фібоначчі числа
Фібоначчі Спіраль: шифроване право природи
Завдяки своїм відносинам, Faris зміг показати, що хоча не існує точок з цілими координатами на двох площинах, кожен з них має дуже близько до нескінченного розсіювання точок з цілими координатами, координати яких є цифри Fibonacci. Кожного разу літак підійшов одну з цих точок Фібоначчі, візерунок виглядає практично таким же чином, як на довідковій точці, яка створює ілюзію точної копії.

Faris також з'ясував, як об'єднати кольори та візерунки природи фотографії з функціями хвилі, щоб включити їх в дизайн візерунків, що призводить до величезної кількості шпалер "false". У вищезгаданій картині можна побачити гілки дерев, які злетів з фото. Видання
Переклад Еріка Кларріх
П.С. І пам'ятайте, що лише змінивши нашу свідомість - разом ми змінюємо світ!
Джерело: geektimes.ru/post/284594/

На лівому зображенні шпалер з симетрією поздовжнього порядку навколо кожного з коричнево-зелених точок. На правому зображенні шпалер з дзеркальною симетрією відносно горизонтальних ліній, що проходять через кожен еліптичний елемент вітражного орнаменту.

П'ятикутна плитка показує безліч прикладів симетрії місцевого п'ятого порядку, але вони не мають шаблонних повторень. При заповненні великих площ на площині, співвідношення кількості широких плиток до кількості вузьких підходів до золотого співвідношення.
Але, хоча можна зробити шпалери з обертальними symmetries другого, третього, четвертого або шостого порядку, неможливо створити шпалери з п'ятою симетрією замовлення (замовлення показує, скільки разів при обертанні 360 градусів візерунок буде самозніматися). Цей обмеження був відомий математикам протягом майже 200 років як кристалографічне обмеження. Геометрія петагона забороняє візерунки з симетрією п'ятого порядку. Так само, як і для замовлень сім або більше.
Тим не менш, найцікавіші візерунки, такі як кахель Penrose, експонують п'ятий порядок локальної симетрії в багатьох місцях і на різних масштабах, але без повторюваних візерунків. Використання методу відрізняється від підходу Penrose, Farris закриває незвичайну геометрію симетрії п'ятого порядку і створив новий набір захоплюючих образів – псевдо-паперовий, не піддається, на перший погляд, кристалографічні обмеження.

Рис. 4. У
Рисунок 4 схожий на контрабанду для кристалографічного обмеження, що має п'ятий порядок обертання симетрії навколо точки А, в той час як візерунок можна змінити на площині в напрямках AB або AC. По суті, Faris пише в своїй статті для журналу Повідомлень Американського Математичного товариства, що ця картина є просто розумною підробкою.
«Ви знаєте, що симетрія, яку ви не можете спостерігати, - говорить Стівен Кеннеді Карлтон Коледж в Міннесота.
П'ятий порядок обертання симетрії навколо точки Здається триматися. Але якщо ви подивитеся уважно, ви можете побачити, що колеса навколо B і C трохи відрізняються від A. Якщо ми змогли відійти від візерунка, щоб побачити більше повторень, очевидні повтори візерунка буде менше і менше, як візерунок навколо точки А, навіть якщо коли-небудь більш переконливі копії А були з'являтися в іншому місці, як на малюнку. 5. Faris показали, що такі ілюзії можуть бути створені на більших масштабах, відходячи від візерунка і повторюючи її певну кількість разів – зокрема, кількість разів, що відповідають номерам в серії Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, ... де кожен наступний номер є сумою попереднього двох), яка також грає роль в геометрії плитки Penrose.

Рис. 5 хв
"Інтелектуальна практика змушує нас розуміти, що це таке децепція, - каже Faris. Я, як він пише в папці, ці зображення "насолодіться нашими думками, щоб вивчити їх і насолоджуватися відкритими повторами."
Faris прийшов з цими підробками, змінивши технологію, за допомогою якого він створив реальний 3-й порядок поворотних симетрій шпалер, таких як рис. 6. Жнівень
Для створення тримісної симетрії, Faris почав працювати в тривимірному просторі, що має одне особливо природне обертання, що проходить через три просторові координати, а поворотні точки в просторі 120 градусів навколо діагоналлю. Faris потім створюються об'ємні візерунки шпалер, які наділяються спеціально підібраними синусоїдами і поєднують їх з попередньо встановленою палітрою кольорів. Ознаки розфарбовувалися в залежності від їх положення на наділених синусоїдах. Потім Faris deduced плоскі шпалери, обмежуючи цей колір на двовимірну площину перпендикулярно осі обертання оригінального простору.
Цей плавний, синусоїдальний підхід до створення шпалерних візерунків відрізняється від традиційного способу копіювання і пасування, говорить Кеннеді. «Це дуже новий спосіб створення симетричних візерунків. й
 р.
р.Рис. 6 хв
Так само процедура виконана в п'ятивимірному просторі, здається, виготовлялася з п'ятою симетрією замовлення. Я дивлюся, Faris дивився, в якому точка не виходить?
У теорії можливий п'ятивимірний простір, хоча складно уявити. Має природний аналог п'ятого порядку обертової симетрії, як і об'ємний простір – симетрія третього порядку. У п'ятивимірному просторі можна вибрати одну з двох площин, кожен перпендикулярно осі обертання і іншої площини. Кожен з них може бути обертається навколо точки 72 або 144 градусів. Здавалося б, важко уявити дві площини і пряму лінію перпендикулярно один одному, але в п'ять розмірах вони мають достатню кількість простору.
Faris розуміє проблему: якщо перпендикулярна площина акуратно розрізається через об'ємний простір, і містить нескінченні шпалери з нескінченною кількістю точок, що володіють цілими координатами, то дві перпендикулярні площини в п'ятивимірному просторі є irrational, і не містять точки з цілими координатами (крім точки посилання). Так як візерунок шпалер, створених з синусоїдів, повторюється через зсуви за цілими цілими, такі площини не впадуть у спадок візерунки в просторах вищого порядку.
«Так, як з'являється в супі,» Faris пише в статті.
Однак ілюзію структури шпалер з'являється на цих двох площинах, завдяки участі так званого золотого співвідношення, ірраціонального числа, що описує напрямки двох площин, і цифри Фібоначчі.
Цікаво: Фібоначчі числа
Фібоначчі Спіраль: шифроване право природи
Завдяки своїм відносинам, Faris зміг показати, що хоча не існує точок з цілими координатами на двох площинах, кожен з них має дуже близько до нескінченного розсіювання точок з цілими координатами, координати яких є цифри Fibonacci. Кожного разу літак підійшов одну з цих точок Фібоначчі, візерунок виглядає практично таким же чином, як на довідковій точці, яка створює ілюзію точної копії.

Faris також з'ясував, як об'єднати кольори та візерунки природи фотографії з функціями хвилі, щоб включити їх в дизайн візерунків, що призводить до величезної кількості шпалер "false". У вищезгаданій картині можна побачити гілки дерев, які злетів з фото. Видання
Переклад Еріка Кларріх
П.С. І пам'ятайте, що лише змінивши нашу свідомість - разом ми змінюємо світ!
Джерело: geektimes.ru/post/284594/