651
如何使不可能壁纸:故事的被禁止的对称
乍一看,拿出墙纸没有更多的困难于执行任务的幼儿园。 设计者可以选择的任何组合的颜色和形状的初始咬然后只是再现它在两个方面。 根据模式的初始片和选择的目的地可能出现,并附加对称性,例如对称的第六次顺序中的第一张照片或反射镜。 这两个模式创建的数学家弗兰克*法里斯,加利福尼亚大学、圣克拉拉。

左边的花纹壁纸折的旋转对称的第六为了围绕各个棕色绿色的玫瑰花。 该权利是图案的墙纸用的镜对称的相对水平线穿过每个椭圆形元的彩色装饰玻璃。
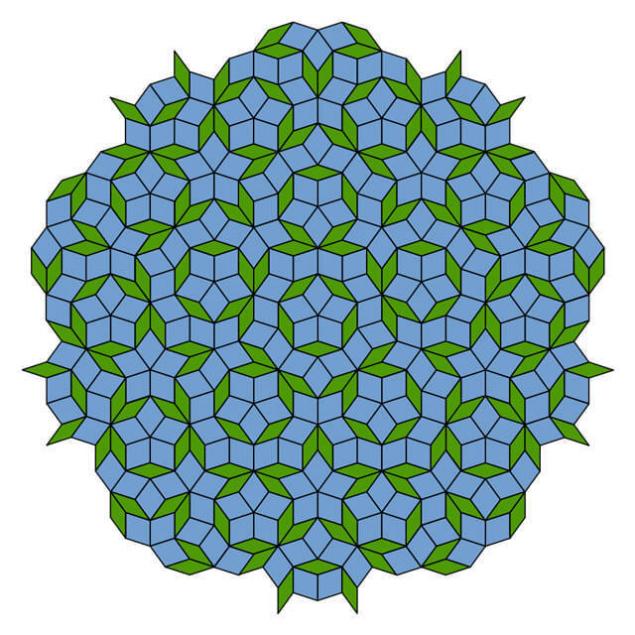
瓦彭罗斯表现出的例子很多的地方对称的第五次序,但是他们没有发现重复的模式。 在填写大面积的平面比广砖数的狭窄的办法的黄金部分。
但是,虽然这是可能做墙纸用的旋转对称的第二、第三、第四或第六数量级,它是不可能创造纸与对称的第五个了(订单的数量表示的时间,在一个360度转动将发生的校准的模式。 另外,高中)。 这种限制的是已知的数学家对于几乎200年为"晶体限制的"。 几何形状的五角大楼的禁止与对称的第五次序。 这同样适用于订单的七个或更多。
但是,最有趣的模式,例如彭罗斯瓷砖,显示出当地称的第五次顺序在许多地方,并在不同尺度,但无需重复的模式。 使用不同的做法彭罗斯的方法,里斯遏制不同寻常的几何形状对称的第五次序和创建一套新的令人兴奋的图像伪纸,不受的,乍一看,这个晶体结构限制。
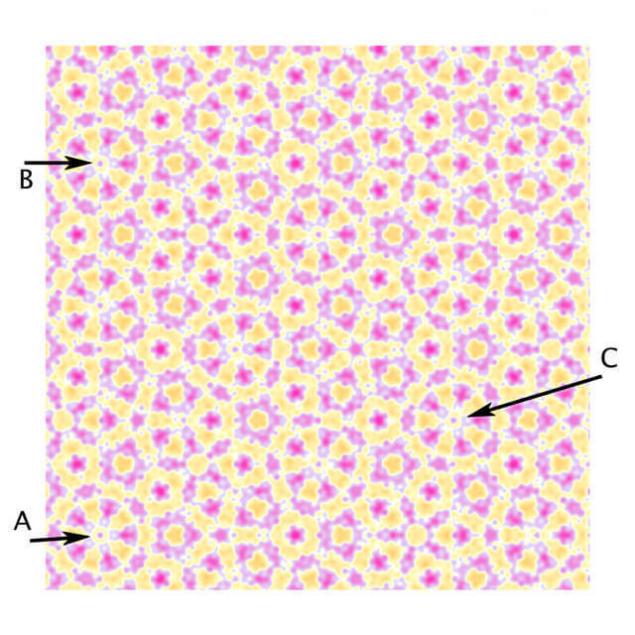
图。 4
第4张照片看起来像一个反的结晶限制,具有旋转对称的第五阶点周围,尽管事实上,该模式可以被转移飞机在方向AB或交流。 事实上,Faris写在他的文章的杂志通知的美国数学学会,这幅画只是一个聪明的假。
"你知道,你是观察对称,是不可能的,说"斯蒂芬*肯尼迪,卡尔顿大学在明尼苏达州。
旋转对称的第五阶点周围的和似乎可以运行。 但如果你仔细看,你可以看到车轮周围点b和C都稍有不同,从A.如果我们可以搬离的模式看到一个更大数量的重复,可见重复的模式将越来越少类似的模式在该地区的一点,即使所有的更多的引人注目的副本,并将出现在其他地方,如在图。 5. Faris已经显示,这样的幻想,可建立在更大的规模,从模式和重复这一定的次数--具体而言,该次数的相应数字从斐波那契数列(1, 1, 2, 3, 5, 8, 13, 21,... 在每个连续的数量的总和以前的两个),其中也发挥作用的几何形状彭罗斯瓷砖。
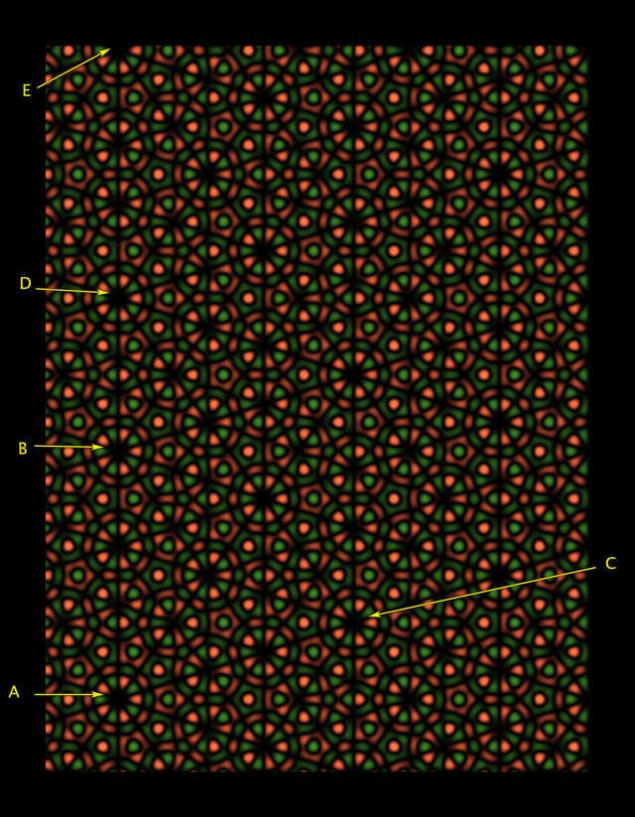
图。 5
"记住我们的理解是,这是某种骗局,"说法里斯。 然而,作为他写的文章,这些图像是"邀请我们的眼睛对他们的研究和享受的几乎完美的重复的"。
Faris出了这些假,不断变化的技术,这是他创造这些墙纸用的旋转对称的3-顺序,例如在图。 6.
创建对称的3阶Faris开始工作,在三维空间,其中有一个特别的自然旋转,使用三个空间的坐标,并转空间中的点120度周围的对角线。 然后Faris创造了三维图案的墙纸,实行一种特殊的方式选择的正弦曲线,并将它们结合有预先选定的调色板。 点颜色的根据自己的位置在的重叠正弦曲线. 然后Faris导致平壁纸的限制性的两个维色飞机的垂直轴线相交的旋转对原来的空间。
这个光滑,使用正弦波的方法来创建的图案的墙纸不同于传统方法的复制和粘贴说,肯尼迪。 "这是一个非常新的方式来创建对称的模式。"

图。 6
同样的程序进行的五个维空间,象它应该导致建立一个模式与对称的第五个了–如果只有我们不知道这是不可能的。 有趣,认为Faris,在什么时候系统发生故障吗?
在理论上,五个维空间可能的,虽然它很难想象的。 他有天然模拟的对称性的旋转的第五顺序,作为在三维空间的对称的三分之一。 在五个维空间可以选择两种飞机,每一个垂直轴旋转和其他飞机。 他们每个人都可以围绕上的一个点72或144度。 它可能看起来难以想象一下两个飞机和直线,互相垂直的,但在五尺寸,它们都具有足够的空间。
Faris实现的是什么问题–如果垂直的平面上整齐切口的三维空间,并包含一个无限的墙纸无数点具有整数的坐标,两个垂直的平面上的五个维空间中的不合理的,并不包含点整数的坐标(除了起始点)。 由于图案的墙纸的创建正弦波使用重复的变化在整数,这样的平面应不继承模式,从不同的空间中的最高的顺序。
"因此,有一个飞往汤写道:"Faris的文章。
然而,这两种飞机出现幻觉的结构的墙纸,感谢参加的所谓的黄金比例,不合理的数量,描述了方向的两个平面,斐波那契数。
也很有趣:斐波那契数字
斐波那契螺旋是加密的法律性质
与他们建立关系时,Faris能够显示,虽然两架飞机并没有点整数的坐标,他们每个人都是非常接近无限的散点整数坐标,这是斐波那契数。 每次的飞机接近这个点,斐波纳契、图案看起来几乎相同的参考点,它创造的幻觉的精确拷贝。

法里斯也想出如何结合的颜色和图案的性质的照片与波的功能,包括在设计的模式,从而有可能获得大量的"虚假"的壁纸。 在上图中可以看到树枝动的照片。出版
翻译:埃丽卡Klarreich
P.S.并记住,只要改变你的想法-我们一起改变世界了。 ©
资料来源:geektimes.ru/post/284594/

左边的花纹壁纸折的旋转对称的第六为了围绕各个棕色绿色的玫瑰花。 该权利是图案的墙纸用的镜对称的相对水平线穿过每个椭圆形元的彩色装饰玻璃。

瓦彭罗斯表现出的例子很多的地方对称的第五次序,但是他们没有发现重复的模式。 在填写大面积的平面比广砖数的狭窄的办法的黄金部分。
但是,虽然这是可能做墙纸用的旋转对称的第二、第三、第四或第六数量级,它是不可能创造纸与对称的第五个了(订单的数量表示的时间,在一个360度转动将发生的校准的模式。 另外,高中)。 这种限制的是已知的数学家对于几乎200年为"晶体限制的"。 几何形状的五角大楼的禁止与对称的第五次序。 这同样适用于订单的七个或更多。
但是,最有趣的模式,例如彭罗斯瓷砖,显示出当地称的第五次顺序在许多地方,并在不同尺度,但无需重复的模式。 使用不同的做法彭罗斯的方法,里斯遏制不同寻常的几何形状对称的第五次序和创建一套新的令人兴奋的图像伪纸,不受的,乍一看,这个晶体结构限制。

图。 4
第4张照片看起来像一个反的结晶限制,具有旋转对称的第五阶点周围,尽管事实上,该模式可以被转移飞机在方向AB或交流。 事实上,Faris写在他的文章的杂志通知的美国数学学会,这幅画只是一个聪明的假。
"你知道,你是观察对称,是不可能的,说"斯蒂芬*肯尼迪,卡尔顿大学在明尼苏达州。
旋转对称的第五阶点周围的和似乎可以运行。 但如果你仔细看,你可以看到车轮周围点b和C都稍有不同,从A.如果我们可以搬离的模式看到一个更大数量的重复,可见重复的模式将越来越少类似的模式在该地区的一点,即使所有的更多的引人注目的副本,并将出现在其他地方,如在图。 5. Faris已经显示,这样的幻想,可建立在更大的规模,从模式和重复这一定的次数--具体而言,该次数的相应数字从斐波那契数列(1, 1, 2, 3, 5, 8, 13, 21,... 在每个连续的数量的总和以前的两个),其中也发挥作用的几何形状彭罗斯瓷砖。

图。 5
"记住我们的理解是,这是某种骗局,"说法里斯。 然而,作为他写的文章,这些图像是"邀请我们的眼睛对他们的研究和享受的几乎完美的重复的"。
Faris出了这些假,不断变化的技术,这是他创造这些墙纸用的旋转对称的3-顺序,例如在图。 6.
创建对称的3阶Faris开始工作,在三维空间,其中有一个特别的自然旋转,使用三个空间的坐标,并转空间中的点120度周围的对角线。 然后Faris创造了三维图案的墙纸,实行一种特殊的方式选择的正弦曲线,并将它们结合有预先选定的调色板。 点颜色的根据自己的位置在的重叠正弦曲线. 然后Faris导致平壁纸的限制性的两个维色飞机的垂直轴线相交的旋转对原来的空间。
这个光滑,使用正弦波的方法来创建的图案的墙纸不同于传统方法的复制和粘贴说,肯尼迪。 "这是一个非常新的方式来创建对称的模式。"

图。 6
同样的程序进行的五个维空间,象它应该导致建立一个模式与对称的第五个了–如果只有我们不知道这是不可能的。 有趣,认为Faris,在什么时候系统发生故障吗?
在理论上,五个维空间可能的,虽然它很难想象的。 他有天然模拟的对称性的旋转的第五顺序,作为在三维空间的对称的三分之一。 在五个维空间可以选择两种飞机,每一个垂直轴旋转和其他飞机。 他们每个人都可以围绕上的一个点72或144度。 它可能看起来难以想象一下两个飞机和直线,互相垂直的,但在五尺寸,它们都具有足够的空间。
Faris实现的是什么问题–如果垂直的平面上整齐切口的三维空间,并包含一个无限的墙纸无数点具有整数的坐标,两个垂直的平面上的五个维空间中的不合理的,并不包含点整数的坐标(除了起始点)。 由于图案的墙纸的创建正弦波使用重复的变化在整数,这样的平面应不继承模式,从不同的空间中的最高的顺序。
"因此,有一个飞往汤写道:"Faris的文章。
然而,这两种飞机出现幻觉的结构的墙纸,感谢参加的所谓的黄金比例,不合理的数量,描述了方向的两个平面,斐波那契数。
也很有趣:斐波那契数字
斐波那契螺旋是加密的法律性质
与他们建立关系时,Faris能够显示,虽然两架飞机并没有点整数的坐标,他们每个人都是非常接近无限的散点整数坐标,这是斐波那契数。 每次的飞机接近这个点,斐波纳契、图案看起来几乎相同的参考点,它创造的幻觉的精确拷贝。

法里斯也想出如何结合的颜色和图案的性质的照片与波的功能,包括在设计的模式,从而有可能获得大量的"虚假"的壁纸。 在上图中可以看到树枝动的照片。出版
翻译:埃丽卡Klarreich
P.S.并记住,只要改变你的想法-我们一起改变世界了。 ©
资料来源:geektimes.ru/post/284594/