667
Como hacer imposibles de fondo de pantalla: la historia prohibida de la simetría
A primera vista inventar fondos de pantalla no es más difícil que realizar tareas del jardín de infantes. Los diseñadores pueden elegir cualquier combinación de colores y formas para la inicial de la pieza, y hacer en los dos sentidos. En función del motivo inicial de la pieza y la selección de destinos que pueden aparecer más de simetría, por ejemplo, la simetría de la sexta de la orden en la primera imagen, o reflejada en la segunda. Ambos patrón creado por el matemático frank Фарисом de la universidad de california de santa clara.

A la izquierda el patrón de papel tapiz con la simetría de rotación de la sexta de la orden alrededor de cada una de marrón-verde de tomas de corriente. A la derecha el patrón de papel tapiz con una simetría respecto a las líneas horizontales que pasan a través de cada elemento elíptico de la ornamentación de la vidriera.
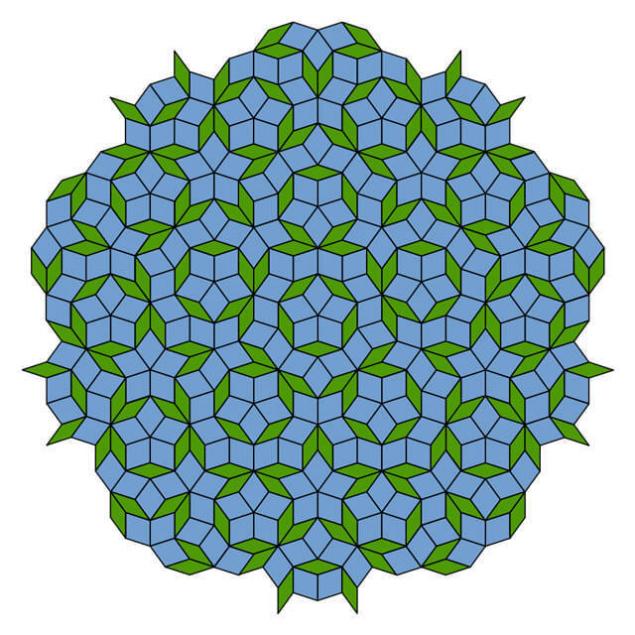
Azulejos Пенроуза demuestran muchos ejemplos local de la simetría de quinto orden, pero ellos no se encuentra repeticiones del motivo. Al rellenar grandes áreas en el plano de la relación de la cantidad de amplias iconos a la cantidad de estrechas se acerca a dorado.
Pero, aunque se puede hacer de fondos de pantalla con вращательными simetrías segundo, tercer, cuarto o sexto órdenes, no se puede crear fondos de pantalla con la simetría de la quinta de la orden (el orden indica la cantidad de veces durante el tiempo de rotación de 360° sucede самосовмещение patrón – aprox. res.). Esta limitación se sabe matemáticos de casi 200 años "кристаллографическое límite". La geometría del pentágono prohíbe a los patrones con la simetría de la quinta de la orden. Lo mismo es cierto para las órdenes de siete y más.
No obstante, los más interesantes patrones, tales como azulejos Пенроуза, manifiestan el local de la simetría de la quinta orden en muchos lugares y en diferentes escalas, sólo que sin los patrones regulares. Utilizando diferente del enfoque Пенроуза método, farris ha conquistado la inusual de la geometría de la simetría de la quinta de la orden y se ha creado un nuevo conjunto de emocionantes imágenes de la pseudo-fondo de pantalla, no pasan, a primera vista, кристаллографическому restricción.
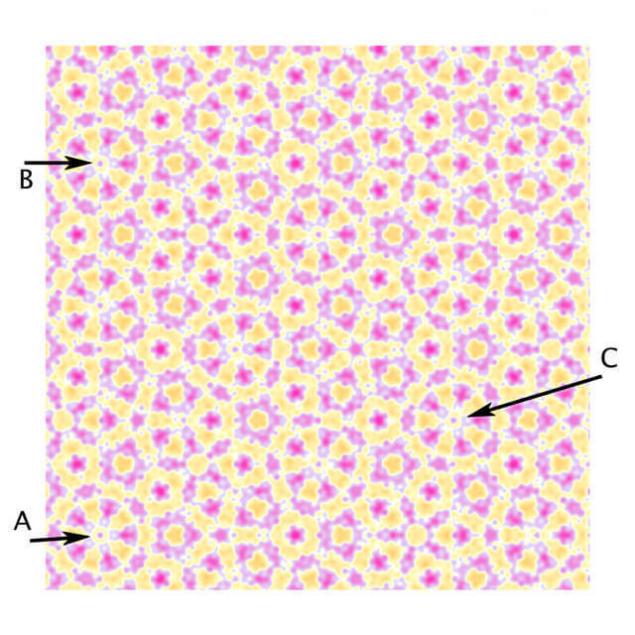
Fig. 4
4º la imagen se ve como контрпример para кристаллографического limitaciones, con giratoria, la simetría de la quinta del orden de alrededor de un punto Y, en caso de que el patrón se puede desplazar en el plano en la dirección de AB o AC. En realidad faris escribe en su artículo para la revista Notices of the American Mathematical Society, que es una imagen – sólo хитроумная falso.
"Usted sabe que se ha observado usted la simetría no es posible", dice stephen kennedy de Карлтонского college en minnesota.
La simetría rotatoria de la quinta del orden de alrededor de un punto Y como se realiza. Pero si se analizan en detalle, se puede observar que las ruedas alrededor de los puntos A y Con un poco diferentes de a. Si pudiéramos alejarse de la trama, para ver la mayor cantidad de repeticiones, lo visible de la repetición de un motivo serían cada vez menos como patrón en el área de los puntos A, incluso si todo el más convincente de la copia Y aparecerían en otros lugares, como en la fig. 5. Faris han demostrado que tales ilusiones se pueden crear y en mayor escala, el alejarse demasiado de la trama y su repetición un número determinado de veces – y en concreto, el número de veces correspondiente a los números de la serie fibonacci (1, 1, 2, 3, 5, 8, 13, 21,... donde cada número es la suma de las dos anteriores), que también juega su papel en la geometría de las baldosas Пенроуза.
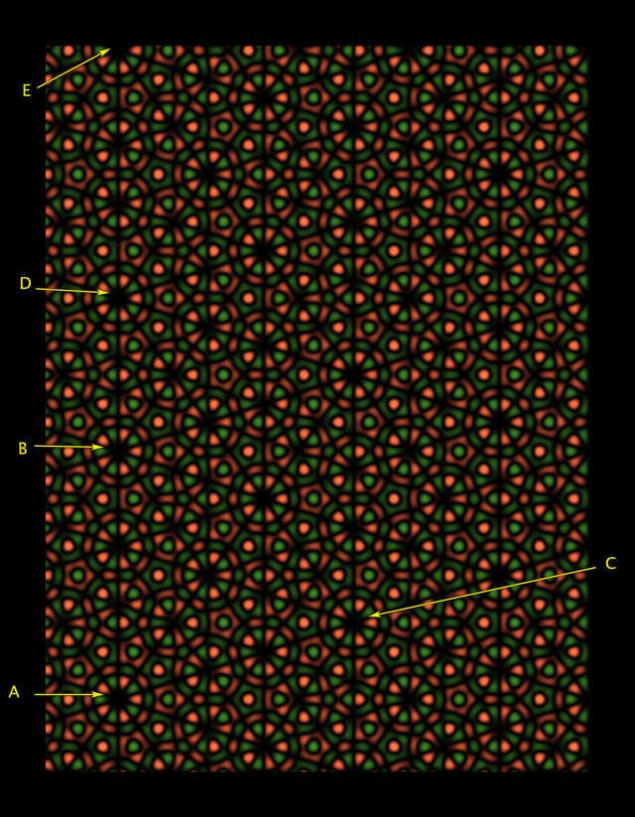
Fig. 5
"La mente nos damos cuenta de que es un engaño", dijo faris. Sin embargo, como se escribe en el artículo, estas imágenes invitan a nuestro punto de vista de su estudio y el disfrute de casi ideales periódicas".
Faris pensaba antes de esas falsificaciones, cambiando la tecnología, a través de la cual se creaba estos fondos de pantalla giratoria con simetría 3 del orden, como en la fig. 6.
Para crear simetría 3 del orden faris comenzó a trabajar en el espacio tridimensional, en el cual hay una especialmente natural de la rotación, перебирающее tres coordenadas espaciales, y вращающее punto en el espacio a 120 grados alrededor de la diagonal. A continuación, faris ha creado tridimensionales patrones de papel tapiz, poniendo de manera especial seleccionados formas de onda y los combina con la elegida de la paleta de los colores. El punto de окрашивались en función de su posición en el impuesto синусоидах. A continuación, faris sacó planas fondos de pantalla, limitando el color de dos dimensiones en un plano perpendicular a la que intersecta el eje de rotación de la original del espacio.
Este suave, utiliza la onda senoidal, el enfoque de la creación de patrones de papel tapiz diferente de la tradicional método de copiar y pegar, dice kennedy. "Esto es una nueva forma de crear patrones simétricos".

Fig. 6
El mismo procedimiento realizado en el пятимерном el espacio, como se debe llevar a la creación de un patrón con la simetría de la quinta orden – si tan sólo no sabíamos que era imposible. Interesante, pensó faris, en algún momento de este sistema falla?
En teoría, пятимерное espacio posible, aunque es difcil imaginar. Tenía una natural análogo de la simetría de rotación de quinto orden, y el espacio tridimensional – la simetría de la tercera. En пятимерном espacio, puede elegir uno de los dos planos, cada uno de los cuales es perpendicular al eje de rotación y otro plano. Cada uno de ellos puede girar alrededor de un punto en el 72 o 144 grados. Puede parecer difícil imaginar dos plano y la recta perpendiculares uno al otro, sino en cinco dimensiones de todos ellos hay suficiente espacio.
Faris di cuenta de que el problema – si perpendicular al plano suavemente rompe el espacio tridimensional, y contiene infinitos fondos de pantalla con un número infinito de puntos con valores enteros coordenadas, dos perpendiculares al plano en пятимерном espacio irracionales, y, en general, no contienen puntos enteros coordenadas (además de punto de referencia). Debido a que el patrón de papel tapiz creado a partir de sinusoides, se repite a través de los cambios en los números enteros, tales plano no heredarán el patrón de la raya de los espacios de orden superior.
"De aquí, y aparece la mosca en la sopa", escribe faris en el artículo.
Sin embargo, en estos dos planos, aparece la ilusión de la estructura del papel pintado, gracias a la participación de lo que se conoce como dorado, irracional número que describe la dirección de la posición de los dos planos, y de los números de fibonacci.
También es interesante: los Números de fibonacci
La ESPIRAL de FIBONACCI cifrada de la ley de la naturaleza
Gracias a sus relaciones, Фарису pudo demostrar que aunque en dos planos y no hay puntos de enteros las coordenadas de cada uno de ellos muy cerca se aproxima a infinito dispersión de puntos enteros coordenadas, las coordenadas que representan los números de fibonacci. Cada vez, cuando el avión se aproxima a uno de esos puntos de fibonacci, la trama se ve casi lo mismo, como en el punto de referencia, que crea la ilusión de una copia exacta.

También faris ha inventado, cómo combinar los colores y los patrones de fotos de la naturaleza de las funciones de onda para incluirlas en el diseño de patrones, el resultado que se puede obtener una gran cantidad de ненастоящих" fondo de pantalla. En la figura siguiente se pueden observar las ramas de los árboles, перекочевавшие con fotos.publicado
Traducción: Erica Klarreich
P. S. Y recuerde, sólo cambiando su conciencia - estamos juntos cambiando el mundo! ©
Fuente: geektimes.ru/post/284594/

A la izquierda el patrón de papel tapiz con la simetría de rotación de la sexta de la orden alrededor de cada una de marrón-verde de tomas de corriente. A la derecha el patrón de papel tapiz con una simetría respecto a las líneas horizontales que pasan a través de cada elemento elíptico de la ornamentación de la vidriera.

Azulejos Пенроуза demuestran muchos ejemplos local de la simetría de quinto orden, pero ellos no se encuentra repeticiones del motivo. Al rellenar grandes áreas en el plano de la relación de la cantidad de amplias iconos a la cantidad de estrechas se acerca a dorado.
Pero, aunque se puede hacer de fondos de pantalla con вращательными simetrías segundo, tercer, cuarto o sexto órdenes, no se puede crear fondos de pantalla con la simetría de la quinta de la orden (el orden indica la cantidad de veces durante el tiempo de rotación de 360° sucede самосовмещение patrón – aprox. res.). Esta limitación se sabe matemáticos de casi 200 años "кристаллографическое límite". La geometría del pentágono prohíbe a los patrones con la simetría de la quinta de la orden. Lo mismo es cierto para las órdenes de siete y más.
No obstante, los más interesantes patrones, tales como azulejos Пенроуза, manifiestan el local de la simetría de la quinta orden en muchos lugares y en diferentes escalas, sólo que sin los patrones regulares. Utilizando diferente del enfoque Пенроуза método, farris ha conquistado la inusual de la geometría de la simetría de la quinta de la orden y se ha creado un nuevo conjunto de emocionantes imágenes de la pseudo-fondo de pantalla, no pasan, a primera vista, кристаллографическому restricción.

Fig. 4
4º la imagen se ve como контрпример para кристаллографического limitaciones, con giratoria, la simetría de la quinta del orden de alrededor de un punto Y, en caso de que el patrón se puede desplazar en el plano en la dirección de AB o AC. En realidad faris escribe en su artículo para la revista Notices of the American Mathematical Society, que es una imagen – sólo хитроумная falso.
"Usted sabe que se ha observado usted la simetría no es posible", dice stephen kennedy de Карлтонского college en minnesota.
La simetría rotatoria de la quinta del orden de alrededor de un punto Y como se realiza. Pero si se analizan en detalle, se puede observar que las ruedas alrededor de los puntos A y Con un poco diferentes de a. Si pudiéramos alejarse de la trama, para ver la mayor cantidad de repeticiones, lo visible de la repetición de un motivo serían cada vez menos como patrón en el área de los puntos A, incluso si todo el más convincente de la copia Y aparecerían en otros lugares, como en la fig. 5. Faris han demostrado que tales ilusiones se pueden crear y en mayor escala, el alejarse demasiado de la trama y su repetición un número determinado de veces – y en concreto, el número de veces correspondiente a los números de la serie fibonacci (1, 1, 2, 3, 5, 8, 13, 21,... donde cada número es la suma de las dos anteriores), que también juega su papel en la geometría de las baldosas Пенроуза.

Fig. 5
"La mente nos damos cuenta de que es un engaño", dijo faris. Sin embargo, como se escribe en el artículo, estas imágenes invitan a nuestro punto de vista de su estudio y el disfrute de casi ideales periódicas".
Faris pensaba antes de esas falsificaciones, cambiando la tecnología, a través de la cual se creaba estos fondos de pantalla giratoria con simetría 3 del orden, como en la fig. 6.
Para crear simetría 3 del orden faris comenzó a trabajar en el espacio tridimensional, en el cual hay una especialmente natural de la rotación, перебирающее tres coordenadas espaciales, y вращающее punto en el espacio a 120 grados alrededor de la diagonal. A continuación, faris ha creado tridimensionales patrones de papel tapiz, poniendo de manera especial seleccionados formas de onda y los combina con la elegida de la paleta de los colores. El punto de окрашивались en función de su posición en el impuesto синусоидах. A continuación, faris sacó planas fondos de pantalla, limitando el color de dos dimensiones en un plano perpendicular a la que intersecta el eje de rotación de la original del espacio.
Este suave, utiliza la onda senoidal, el enfoque de la creación de patrones de papel tapiz diferente de la tradicional método de copiar y pegar, dice kennedy. "Esto es una nueva forma de crear patrones simétricos".

Fig. 6
El mismo procedimiento realizado en el пятимерном el espacio, como se debe llevar a la creación de un patrón con la simetría de la quinta orden – si tan sólo no sabíamos que era imposible. Interesante, pensó faris, en algún momento de este sistema falla?
En teoría, пятимерное espacio posible, aunque es difcil imaginar. Tenía una natural análogo de la simetría de rotación de quinto orden, y el espacio tridimensional – la simetría de la tercera. En пятимерном espacio, puede elegir uno de los dos planos, cada uno de los cuales es perpendicular al eje de rotación y otro plano. Cada uno de ellos puede girar alrededor de un punto en el 72 o 144 grados. Puede parecer difícil imaginar dos plano y la recta perpendiculares uno al otro, sino en cinco dimensiones de todos ellos hay suficiente espacio.
Faris di cuenta de que el problema – si perpendicular al plano suavemente rompe el espacio tridimensional, y contiene infinitos fondos de pantalla con un número infinito de puntos con valores enteros coordenadas, dos perpendiculares al plano en пятимерном espacio irracionales, y, en general, no contienen puntos enteros coordenadas (además de punto de referencia). Debido a que el patrón de papel tapiz creado a partir de sinusoides, se repite a través de los cambios en los números enteros, tales plano no heredarán el patrón de la raya de los espacios de orden superior.
"De aquí, y aparece la mosca en la sopa", escribe faris en el artículo.
Sin embargo, en estos dos planos, aparece la ilusión de la estructura del papel pintado, gracias a la participación de lo que se conoce como dorado, irracional número que describe la dirección de la posición de los dos planos, y de los números de fibonacci.
También es interesante: los Números de fibonacci
La ESPIRAL de FIBONACCI cifrada de la ley de la naturaleza
Gracias a sus relaciones, Фарису pudo demostrar que aunque en dos planos y no hay puntos de enteros las coordenadas de cada uno de ellos muy cerca se aproxima a infinito dispersión de puntos enteros coordenadas, las coordenadas que representan los números de fibonacci. Cada vez, cuando el avión se aproxima a uno de esos puntos de fibonacci, la trama se ve casi lo mismo, como en el punto de referencia, que crea la ilusión de una copia exacta.

También faris ha inventado, cómo combinar los colores y los patrones de fotos de la naturaleza de las funciones de onda para incluirlas en el diseño de patrones, el resultado que se puede obtener una gran cantidad de ненастоящих" fondo de pantalla. En la figura siguiente se pueden observar las ramas de los árboles, перекочевавшие con fotos.publicado
Traducción: Erica Klarreich
P. S. Y recuerde, sólo cambiando su conciencia - estamos juntos cambiando el mundo! ©
Fuente: geektimes.ru/post/284594/