1215
对称的性质
几个世纪以来,对称仍是一个课题着迷的哲学家,天文学家,数学家,艺术家,建筑师和物理学家。古希腊人完全着迷于它 - 即使在今天,我们通常从规划我们的家具的位置,凿毛面对的是一个对称的一切。

西兰花romanesco
也许看到西兰花romanesco在商店里,你在想,这是转基因食品多了一个样本。但事实上,这是大自然的分形对称的另一个例子。西兰花的每花序具有对数螺旋的图案。宝塔花菜是在外观和味道和一致性,相似 - 花椰菜。它含有丰富的类胡萝卜素和维生素C和钾,这使得它不仅美观,而且还健康食品。

蜂窝
千百年来,人们一直想知道理想的六边形蜂窝,想知道蜜蜂如何能本能地创造,人们只能通过直尺和圆规来重现形式。如何以及为什么蜜蜂有一个强烈的愿望来创建六边形?数学家认为,这是理想的形式,这使得他们存储蜂蜜的最大可能量,使用蜡的最小量。在任何情况下,这是自然的所有产品,这是相当不错的印象深刻。

向日葵
向日葵可以夸耀径向对称的和有趣的对称型,称为斐波那契序列。斐波那契序列:1,2,3,5,8,13,21,24,55,89,144,等等。 (每个数字是前两个数字的总和)。如果我们不快点计入向日葵种子的数量,我们会发现,在斐波那契序列的原则,不断增加螺旋的数量。在自然界中,也有很多植物(包括花椰菜romanesco),花瓣,种子,并符合此序列叶,因此很难找到具有四个叶子的三叶草。
但是,为什么向日葵等植物符合数学法则?像六边形蜂巢,这一切 - 效率问题

鹦鹉螺
除了植物,一些动物,如鹦鹉螺,满足斐波纳契数列。鹦鹉螺壳曲折的“斐波纳契螺旋。”壳试图维持相同的比例的形状,使其能够在整个生命维持它(而不是人谁正在改变寿命的比例)。并非所有有鹦鹉螺壳,列队在斐波那契的规则,但他们都满足了对数螺旋线。
在您pozaviduete贝类数学家,记住,他们不这样做的目的,只是一种形式的最合理的他们。

宠物
大多数动物具有双侧对称的,这意味着它们可以分成相同的两半。即使是人谁也左右对称,有些科学家认为,人类的对称性是影响我们的感知美的最重要的因素。换句话说,如果你有一个片面的人,我们希望,这是其他优秀品质补偿。
在努力吸引合作伙伴,如孔雀有的达到完全对称。达尔文是通过这种鸟正恼火,并在一封信中写道,“在一个孔雀的尾羽的类型,每当我看着它,让我感到恶心!”达尔文,尾巴显得繁琐,没有进化的意义,因为它不符合他的理论“适者生存”。他大发雷霆,直到他想出了性选择理论,其中指出,动物发展的某些功能,以增加交配的机会。为什么孔雀有不同的工具来吸引合作伙伴。

网络
大约有5000种蜘蛛,并且他们创造一个近乎完美的圆刀片径向支撑线几乎等距螺旋布料抓猎物。科学家们不知道为什么蜘蛛这么喜欢几何,作为试验表明,圆带不引诱的食物比不规则形状的网络更好。科学家认为,径向对称分布冲击力当受害者获取在网络上,从而导致破坏少。

麦田怪圈
给几个骗子板割草机和节约黑暗里,你会看到,人们还可以创建一个对称的形状。由于事实,麦田怪圈是复杂的设计和令人难以置信的对称性,即使在社会各界的认可和切磋球技的创造者,许多人仍然认为它没有外星人。
随着社会的复杂性越来越清晰自己的人工来源。这是不合逻辑的假设,外星人将让你的帖子更加困难的时候,我们无法破译即使是其中的第一个。
不管他们是如何到达那里,麦田怪圈很好的治疗,主要是因为它们的几何是令人印象深刻。

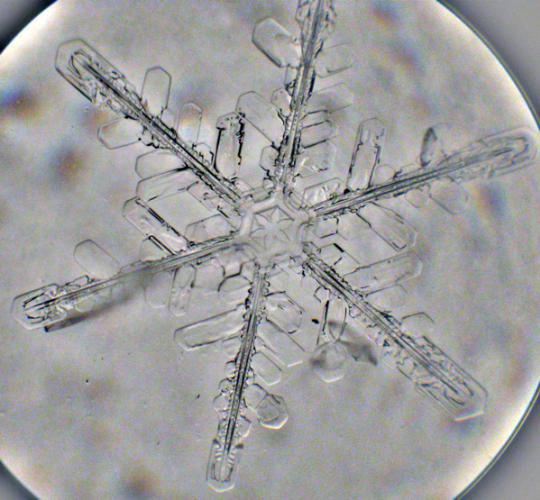
雪花
即使如此微小的教育,像雪花一样,被对称的法律管辖,为广大有雪花的六角形对称性。这种情况发生时,部分是由于水分子如何排队时固化(结晶)。水分子变成固态,形成了弱氢键,它们排列在该平衡吸引和排斥的力有序排列,形成雪花六边形形状。然而,每个雪花是对称的,但没有雪花是不是像另一个。这是因为从空中落下,每个雪花正经历着独特的大气条件下,使排列在以某种方式的结晶。
银河系
正如我们所看到的,对称性和数学模型存在几乎无处不在,但被我们这个星球的自然法则的限制?显然,没有。最近开在银河系的边缘一个新的部分,而天文学家认为,星系是他自己几乎完美的镜像。

太阳,月亮
的对称性
考虑到太阳的直径为1,4万公里,而月球 - 3474公里,看来几乎是不可能的,月球可以遮挡阳光,并为我们提供了约五日食每两年一次。它是如何工作的?巧合的是,伴随着的事实是,太阳的宽度比月亮,太阳和400倍放大大约400倍更远。对称性规定,太阳和月亮得到同样的大小,从地球上看到的,所以月球可以覆盖太阳。当然,从地球到太阳的距离增加,所以有时我们看到和环偏食。但每次一到两年,需要精确对准,与我们共同见证被称为日全食壮观的事件。天文学家不知道如何共同的其他行星之间的这种对称,但他们认为这是相当罕见的。尽管如此,我们不应该认为我们是特殊的,偶然的,因为这一切的问题。例如,每年月球远离地面,这意味着数十亿年前,每次日食是日全食约4厘米。如果事情继续下去这样的日全食,最终,消失,它会伴随着日环食的消失。事实证明,我们只是在合适的时候看到这种现象在正确的地方。

资料来源:bigpicture.ru

西兰花romanesco
也许看到西兰花romanesco在商店里,你在想,这是转基因食品多了一个样本。但事实上,这是大自然的分形对称的另一个例子。西兰花的每花序具有对数螺旋的图案。宝塔花菜是在外观和味道和一致性,相似 - 花椰菜。它含有丰富的类胡萝卜素和维生素C和钾,这使得它不仅美观,而且还健康食品。

蜂窝
千百年来,人们一直想知道理想的六边形蜂窝,想知道蜜蜂如何能本能地创造,人们只能通过直尺和圆规来重现形式。如何以及为什么蜜蜂有一个强烈的愿望来创建六边形?数学家认为,这是理想的形式,这使得他们存储蜂蜜的最大可能量,使用蜡的最小量。在任何情况下,这是自然的所有产品,这是相当不错的印象深刻。

向日葵
向日葵可以夸耀径向对称的和有趣的对称型,称为斐波那契序列。斐波那契序列:1,2,3,5,8,13,21,24,55,89,144,等等。 (每个数字是前两个数字的总和)。如果我们不快点计入向日葵种子的数量,我们会发现,在斐波那契序列的原则,不断增加螺旋的数量。在自然界中,也有很多植物(包括花椰菜romanesco),花瓣,种子,并符合此序列叶,因此很难找到具有四个叶子的三叶草。
但是,为什么向日葵等植物符合数学法则?像六边形蜂巢,这一切 - 效率问题

鹦鹉螺
除了植物,一些动物,如鹦鹉螺,满足斐波纳契数列。鹦鹉螺壳曲折的“斐波纳契螺旋。”壳试图维持相同的比例的形状,使其能够在整个生命维持它(而不是人谁正在改变寿命的比例)。并非所有有鹦鹉螺壳,列队在斐波那契的规则,但他们都满足了对数螺旋线。
在您pozaviduete贝类数学家,记住,他们不这样做的目的,只是一种形式的最合理的他们。

宠物
大多数动物具有双侧对称的,这意味着它们可以分成相同的两半。即使是人谁也左右对称,有些科学家认为,人类的对称性是影响我们的感知美的最重要的因素。换句话说,如果你有一个片面的人,我们希望,这是其他优秀品质补偿。
在努力吸引合作伙伴,如孔雀有的达到完全对称。达尔文是通过这种鸟正恼火,并在一封信中写道,“在一个孔雀的尾羽的类型,每当我看着它,让我感到恶心!”达尔文,尾巴显得繁琐,没有进化的意义,因为它不符合他的理论“适者生存”。他大发雷霆,直到他想出了性选择理论,其中指出,动物发展的某些功能,以增加交配的机会。为什么孔雀有不同的工具来吸引合作伙伴。

网络
大约有5000种蜘蛛,并且他们创造一个近乎完美的圆刀片径向支撑线几乎等距螺旋布料抓猎物。科学家们不知道为什么蜘蛛这么喜欢几何,作为试验表明,圆带不引诱的食物比不规则形状的网络更好。科学家认为,径向对称分布冲击力当受害者获取在网络上,从而导致破坏少。

麦田怪圈
给几个骗子板割草机和节约黑暗里,你会看到,人们还可以创建一个对称的形状。由于事实,麦田怪圈是复杂的设计和令人难以置信的对称性,即使在社会各界的认可和切磋球技的创造者,许多人仍然认为它没有外星人。
随着社会的复杂性越来越清晰自己的人工来源。这是不合逻辑的假设,外星人将让你的帖子更加困难的时候,我们无法破译即使是其中的第一个。
不管他们是如何到达那里,麦田怪圈很好的治疗,主要是因为它们的几何是令人印象深刻。

雪花
即使如此微小的教育,像雪花一样,被对称的法律管辖,为广大有雪花的六角形对称性。这种情况发生时,部分是由于水分子如何排队时固化(结晶)。水分子变成固态,形成了弱氢键,它们排列在该平衡吸引和排斥的力有序排列,形成雪花六边形形状。然而,每个雪花是对称的,但没有雪花是不是像另一个。这是因为从空中落下,每个雪花正经历着独特的大气条件下,使排列在以某种方式的结晶。

银河系
正如我们所看到的,对称性和数学模型存在几乎无处不在,但被我们这个星球的自然法则的限制?显然,没有。最近开在银河系的边缘一个新的部分,而天文学家认为,星系是他自己几乎完美的镜像。

太阳,月亮
的对称性
考虑到太阳的直径为1,4万公里,而月球 - 3474公里,看来几乎是不可能的,月球可以遮挡阳光,并为我们提供了约五日食每两年一次。它是如何工作的?巧合的是,伴随着的事实是,太阳的宽度比月亮,太阳和400倍放大大约400倍更远。对称性规定,太阳和月亮得到同样的大小,从地球上看到的,所以月球可以覆盖太阳。当然,从地球到太阳的距离增加,所以有时我们看到和环偏食。但每次一到两年,需要精确对准,与我们共同见证被称为日全食壮观的事件。天文学家不知道如何共同的其他行星之间的这种对称,但他们认为这是相当罕见的。尽管如此,我们不应该认为我们是特殊的,偶然的,因为这一切的问题。例如,每年月球远离地面,这意味着数十亿年前,每次日食是日全食约4厘米。如果事情继续下去这样的日全食,最终,消失,它会伴随着日环食的消失。事实证明,我们只是在合适的时候看到这种现象在正确的地方。

资料来源:bigpicture.ru























