205
La tarea que los chinos de segundo grado resuelven en un instante: prueba tu fuerza
Las tareas de desarrollo para los niños son buenas porque te hacen pensar duro. Los padres están indignados y desconcertados: “¿Qué desastre, cómo se puede resolver esto sin Xes y ecuaciones?” ¡Pero hay una manera, por supuesto! No es el que estamos acostumbrados. De lo contrario, ¿cómo podría resolver el problema del gato y la tortuga al instante por estudiantes de primaria en China?
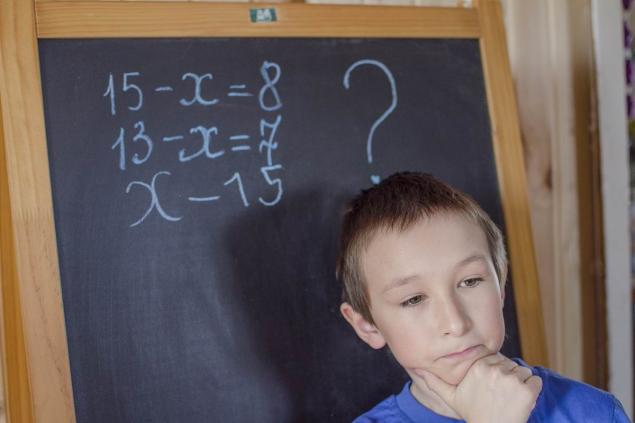
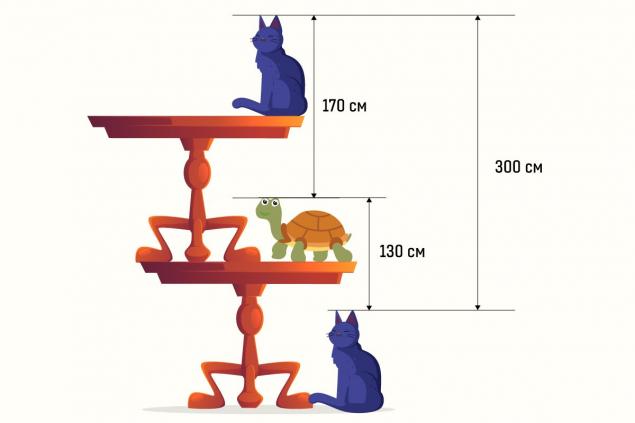
Entonces, necesitas encontrar la altura de la mesa en la imagen. En cuanto a las condiciones, son: desde la cabeza de una tortuga sentada bajo una mesa a la cabeza de un gato sentado sobre una mesa, exactamente 170 cm. La distancia de la cabeza del gato sentado debajo de la mesa a la cabeza de la tortuga sentada sobre la mesa es de 130 cm.
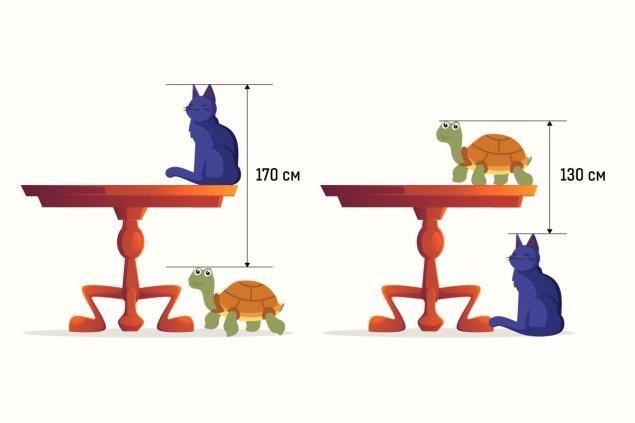
Para un adulto familiarizado con el álgebra, el primer impulso es construir un sistema de ecuaciones. Said, hecho. Denotamos la altura de la mesa, la altura de la tortuga - y, la altura del gato - z.

Luego la figura izquierda toma la forma - y + z = 170 cm. Para obtener 170 cm, necesita restar la altura de la tortuga de la altura de la mesa y añadir la altura del gato. Del mismo modo, presentamos la imagen correcta. Sólo desde la altura de la mesa, restamos la altura del gato, y agregamos la altura de la tortuga. Resulta - z + y = 130 cm.
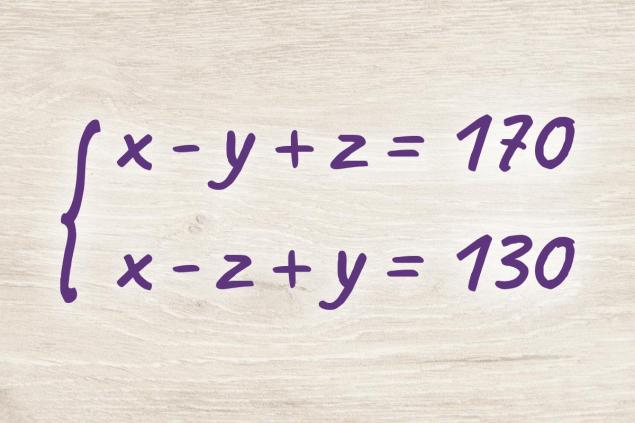
Ya no hay necesidad de hacer suposiciones. Queda por resolver el sistema de ecuaciones, como nos enseñaron en las lecciones de matemáticas escolares. Usando la adición articulada en el sistema de ecuaciones, obtenemos - y + z + y - z = 170 + 130. Por lo tanto 2x = 300 y x = 150. Respuesta: altura de mesa - 150 cm.
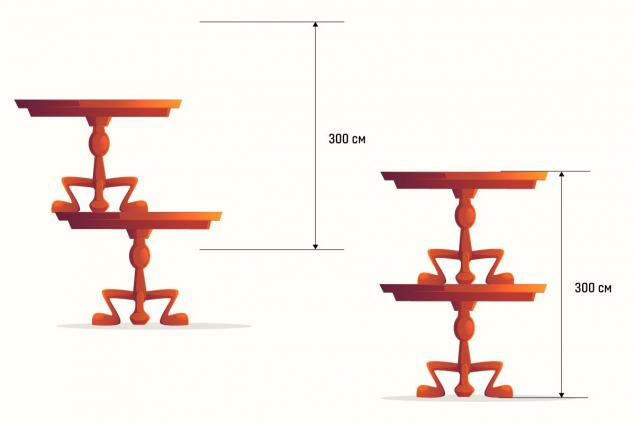
Los estudiantes jóvenes que aún no han aprobado el sistema de ecuaciones también pueden resolver el problema. Pero de una manera más simple y más visual, que, sin embargo, requiere cierta imaginación. Para hacer esto, necesitas poner mentalmente la imagen derecha a la izquierda. El resultado que representamos en la imagen siguiente.
Se muestra claramente que si se añade la altura del gato para duplicar la altura de la mesa, y luego restarlo, se obtiene 300 centímetros. En consecuencia, dos mesas son de 300 cm de altura y una de 150.
Esperamos que la solución de este problema no le parezca extremadamente difícil, y el proceso en sí mismo fue agradable y emocionante. Para hacer frente sin ecuaciones, tuvimos que apagar el camino golpeado y pensar creativamente y fuera de la caja. Esta experiencia ayuda a encontrar soluciones inusuales, logrando el resultado de la manera más corta posible.
Entonces, necesitas encontrar la altura de la mesa en la imagen. En cuanto a las condiciones, son: desde la cabeza de una tortuga sentada bajo una mesa a la cabeza de un gato sentado sobre una mesa, exactamente 170 cm. La distancia de la cabeza del gato sentado debajo de la mesa a la cabeza de la tortuga sentada sobre la mesa es de 130 cm.

Para un adulto familiarizado con el álgebra, el primer impulso es construir un sistema de ecuaciones. Said, hecho. Denotamos la altura de la mesa, la altura de la tortuga - y, la altura del gato - z.

Luego la figura izquierda toma la forma - y + z = 170 cm. Para obtener 170 cm, necesita restar la altura de la tortuga de la altura de la mesa y añadir la altura del gato. Del mismo modo, presentamos la imagen correcta. Sólo desde la altura de la mesa, restamos la altura del gato, y agregamos la altura de la tortuga. Resulta - z + y = 130 cm.
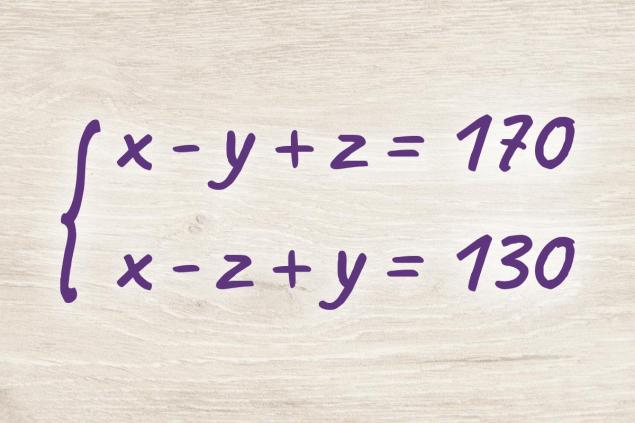
Ya no hay necesidad de hacer suposiciones. Queda por resolver el sistema de ecuaciones, como nos enseñaron en las lecciones de matemáticas escolares. Usando la adición articulada en el sistema de ecuaciones, obtenemos - y + z + y - z = 170 + 130. Por lo tanto 2x = 300 y x = 150. Respuesta: altura de mesa - 150 cm.
Los estudiantes jóvenes que aún no han aprobado el sistema de ecuaciones también pueden resolver el problema. Pero de una manera más simple y más visual, que, sin embargo, requiere cierta imaginación. Para hacer esto, necesitas poner mentalmente la imagen derecha a la izquierda. El resultado que representamos en la imagen siguiente.

Se muestra claramente que si se añade la altura del gato para duplicar la altura de la mesa, y luego restarlo, se obtiene 300 centímetros. En consecuencia, dos mesas son de 300 cm de altura y una de 150.

Esperamos que la solución de este problema no le parezca extremadamente difícil, y el proceso en sí mismo fue agradable y emocionante. Para hacer frente sin ecuaciones, tuvimos que apagar el camino golpeado y pensar creativamente y fuera de la caja. Esta experiencia ayuda a encontrar soluciones inusuales, logrando el resultado de la manera más corta posible.
Acerca de lo que los futuros cataclismos advirtieron al profeta Raymond Aguilera
¿Quién era el predictor monje Abel y qué maravillosas revelaciones sobre el futuro que recibimos de él