197
The task that Chinese second graders solve in an instant: test your strength
Developmental tasks for children are good because they make you think hard. Parents are indignant and puzzled: “What a mess, how can this be solved without Xes and equations?” But there is a way, of course! He's just not the one we're used to. Otherwise, how could the cat and turtle problem be solved instantly by elementary school students in China?
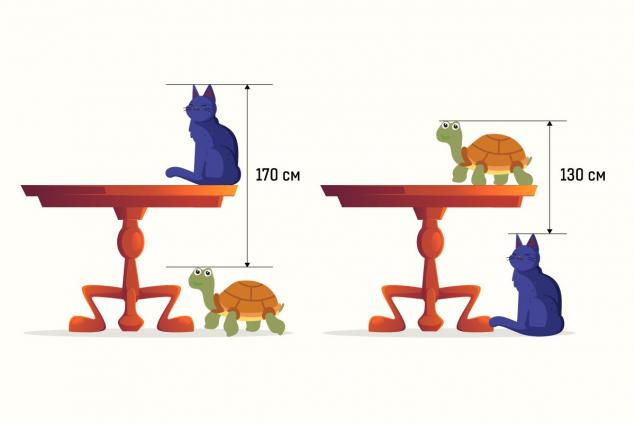
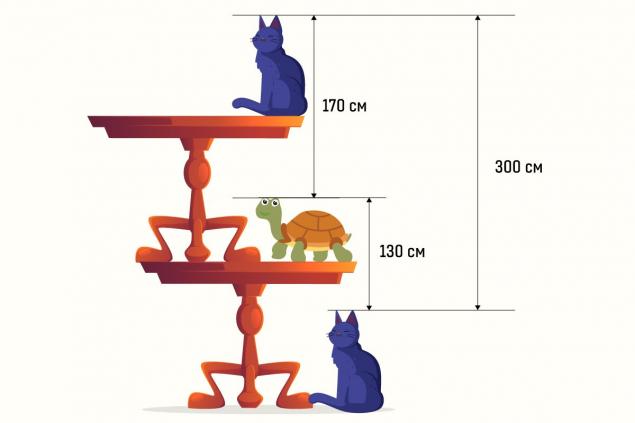
So, you need to find the height of the table in the picture. As for the conditions, they are: from the head of a turtle sitting under a table to the head of a cat sitting on a table, exactly 170 cm. The distance from the head of the cat sitting under the table to the head of the turtle sitting on the table is 130 cm.
For an adult familiar with algebra, the first impulse is to construct a system of equations. Said, done. Let's denote the height of the table, the height of the turtle - y, the height of the cat - z.

Then the left figure takes the form - y + z = 170 cm. To get 170 cm, you need to subtract the height of the turtle from the height of the table and add the height of the cat. Similarly, we present the right picture. Only from the height of the table, we subtract the height of the cat, and add the height of the turtle. It turns out - z + y = 130 cm.
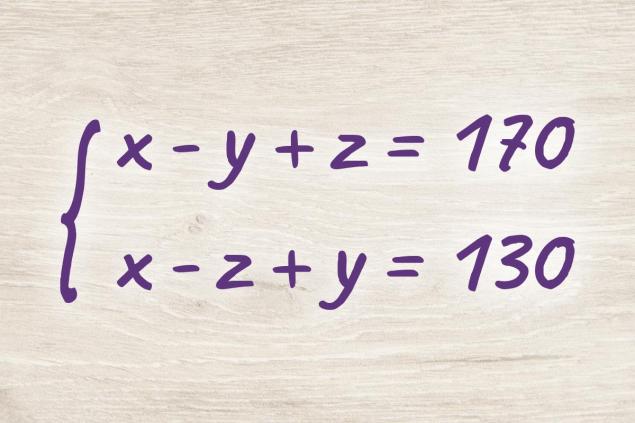
There is no need to make assumptions anymore. It remains to solve the system of equations, as we were taught in school mathematics lessons. Using the articulated addition in the system of equations, we get - y + z + y - z = 170 + 130. Hence 2x = 300 and x = 150. Answer: table height - 150 cm.
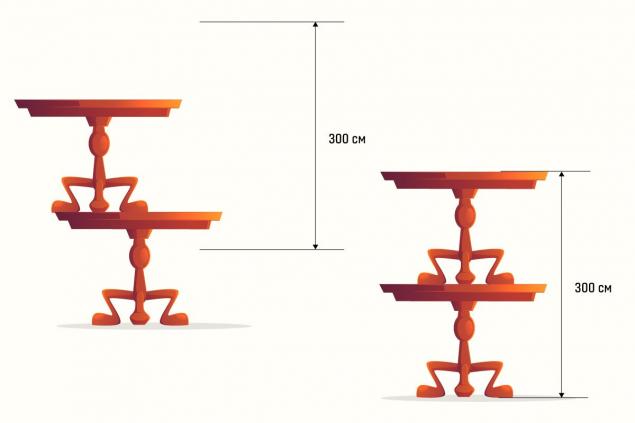
Junior students who have not yet passed the system of equations can also solve the problem. But in a simpler and more visual way, which, however, requires some imagination. To do this, you need to mentally put the right picture on the left. The result we depicted in the picture below.
It clearly shows that if you add the height of the cat to double the height of the table, and then subtract it, you get 300 centimeters. Consequently, two tables are 300 cm high and one is 150.
We hope that the solution of this problem did not seem to you extremely difficult, and the process itself was pleasant and exciting. To cope without equations, we had to turn off the beaten path and think creatively and outside the box. Such experience helps to find unusual solutions, achieving the result in the shortest possible way.
So, you need to find the height of the table in the picture. As for the conditions, they are: from the head of a turtle sitting under a table to the head of a cat sitting on a table, exactly 170 cm. The distance from the head of the cat sitting under the table to the head of the turtle sitting on the table is 130 cm.

For an adult familiar with algebra, the first impulse is to construct a system of equations. Said, done. Let's denote the height of the table, the height of the turtle - y, the height of the cat - z.

Then the left figure takes the form - y + z = 170 cm. To get 170 cm, you need to subtract the height of the turtle from the height of the table and add the height of the cat. Similarly, we present the right picture. Only from the height of the table, we subtract the height of the cat, and add the height of the turtle. It turns out - z + y = 130 cm.
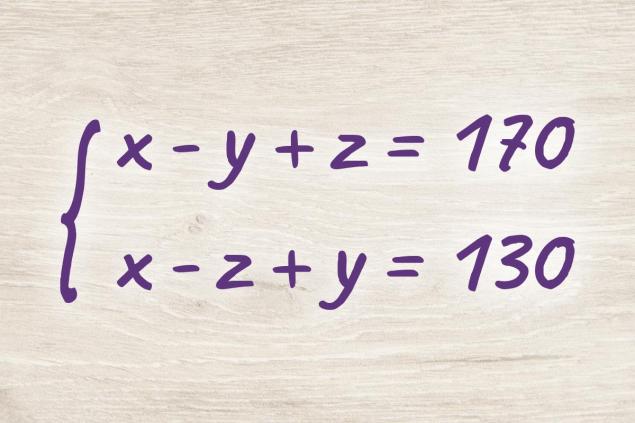
There is no need to make assumptions anymore. It remains to solve the system of equations, as we were taught in school mathematics lessons. Using the articulated addition in the system of equations, we get - y + z + y - z = 170 + 130. Hence 2x = 300 and x = 150. Answer: table height - 150 cm.
Junior students who have not yet passed the system of equations can also solve the problem. But in a simpler and more visual way, which, however, requires some imagination. To do this, you need to mentally put the right picture on the left. The result we depicted in the picture below.

It clearly shows that if you add the height of the cat to double the height of the table, and then subtract it, you get 300 centimeters. Consequently, two tables are 300 cm high and one is 150.

We hope that the solution of this problem did not seem to you extremely difficult, and the process itself was pleasant and exciting. To cope without equations, we had to turn off the beaten path and think creatively and outside the box. Such experience helps to find unusual solutions, achieving the result in the shortest possible way.
About what future cataclysms warned the prophet Raymond Aguilera
Who was the monk-predictor Abel and what wonderful revelations about the future we got from him