229
¿Por qué hay un primer grado en la escuela como un instituto?
Tomamos estos complejos problemas matemáticos de los libros de texto de la escuela primaria ordinaria. Los padres están indignados y desconcertados: “¿Qué desastre, cómo resolverlos sin X y sistemas de ecuaciones?” ?

Parece que Alla Borisovna sabía de este problema en 1980. Hoy, el primer grado es una especie de institución. Pero a diferencia del doctor emocional en "Primer Graduate Songs", no vamos a estar a cargo de la tarea de llorar. Intentaremos encontrar soluciones sencillas para ellos.
Problemas matemáticos complejos Círculos, triángulos y cuadrados El problema para la primera clase con un asterisco (aumento de complejidad). Es necesario encontrar la suma del círculo, triángulo y cuadrado.
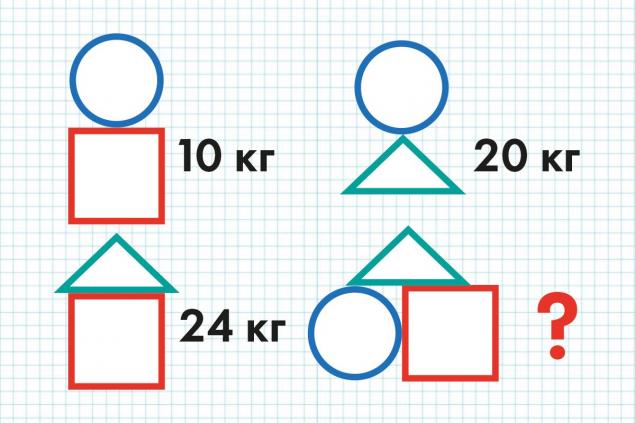
Para un adulto familiarizado con el álgebra, el primer impulso es construir un sistema de tres ecuaciones. Si el círculo es x, el cuadrado es y, y el triángulo es z, obtenemos:
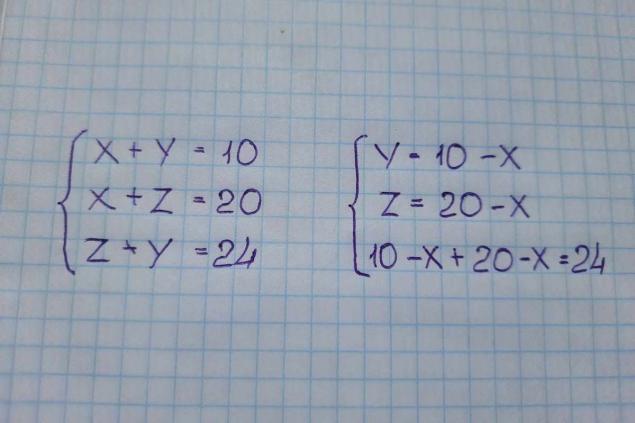
De ahí 30 – 2x = 24; 2x = 6; x = 3. El círculo (x) es 3, por lo que el cuadrado (y) es 7, y el triángulo (z) es 17. La suma del círculo, triángulo y cuadrado nos da 27 kg.
Pero los sistemas de ecuaciones comienzan a aprender sólo en las clases de álgebra en el séptimo grado. ¿Hay una solución más simple? Algunos padres en los comentarios sugieren resolver el problema seleccionando valores. Pero para mí, se siente más como una adivinación que una solución.
Veamos nuestras cifras de nuevo. En los tres primeros dibujos tenemos dos cuadrados, dos círculos y dos triángulos. Todo esto suma hasta 54. Así que el círculo de media cuadra y el triángulo es 27 (54:2 = 27).

O de otra manera: un círculo más un cuadrado de 10, y un triángulo más un cuadrado de 24, significa un triángulo 14 kilogramos más pesado que un círculo. Es decir, si el círculo se toma como x, entonces el triángulo es x + 14. Luego x + x + 14 = 20; x = 3, y así sucesivamente.
Katya y 4 postales Este problema que encontré en las asignaciones que mi hijo tercer grado tuvo que realizar en las vacaciones de verano. Esto no es la binomy de Newton, pero ¿cómo lo hace sin ecuaciones y sólo métodos elementales de la escuela? ¿Y cuántos niños serán capaces de resolver esto sin un padre que es “fuerte en matemáticas”?
475183.
No puedes hacerlo sin variables otra vez. Supongamos que la primera postal costó un rublos, el segundo - b, el tercero - c, el cuarto - d. Luego b+c+d=42; a+c+d=40; a+b+d=38; a+b+c=36. ¿Qué debemos hacer con esta riqueza?

Está claro que hay que añadir algo, pero no está muy claro qué con qué y por qué motivos. Digamos que armamos todas las partes izquierdas de nuestras expresiones. Consigue 3a+3b+3c+3d o 3(a+d+c+d). Puedes ver que esto es triple el valor de todas las cartas. Desde aquí encontramos su valor (42+40+38+36):3=52 rublos.
Ahora es cuestión de tecnología. 52-42=10 es la primera postal; 52-40=12 es la segunda postal; 52-38=14 es la tercera postal; 52-36=16 es la cuarta postal. Tenga en cuenta que en los comentarios, los adultos inteligentes con dos más altos sugieren “hacer un gráfico lineal simple”, “solver por el método de una calabaza no científica”, “más a menudo acercarse a la tarea, la tarea, dicen, y los huevos no valen la pena. ”

¿Crees que estas tareas ayudan a los estudiantes a desarrollar la lógica o desalentar completamente el deseo de aprender? Es fácil para un adulto, pero ¿pueden explicarlo a un niño? Un niño no decidirá una vez, no decidirá dos veces, y concluirá que nunca será capaz de entender esta terrible matemática. Y la madre suspira y dice: "Qué puedes hacer, mi hijo es un humanitario, no se le da ..."

Parece que Alla Borisovna sabía de este problema en 1980. Hoy, el primer grado es una especie de institución. Pero a diferencia del doctor emocional en "Primer Graduate Songs", no vamos a estar a cargo de la tarea de llorar. Intentaremos encontrar soluciones sencillas para ellos.
Problemas matemáticos complejos Círculos, triángulos y cuadrados El problema para la primera clase con un asterisco (aumento de complejidad). Es necesario encontrar la suma del círculo, triángulo y cuadrado.

Para un adulto familiarizado con el álgebra, el primer impulso es construir un sistema de tres ecuaciones. Si el círculo es x, el cuadrado es y, y el triángulo es z, obtenemos:
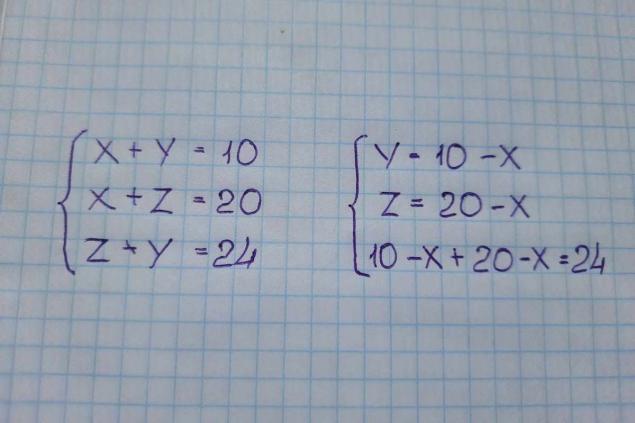
De ahí 30 – 2x = 24; 2x = 6; x = 3. El círculo (x) es 3, por lo que el cuadrado (y) es 7, y el triángulo (z) es 17. La suma del círculo, triángulo y cuadrado nos da 27 kg.
Pero los sistemas de ecuaciones comienzan a aprender sólo en las clases de álgebra en el séptimo grado. ¿Hay una solución más simple? Algunos padres en los comentarios sugieren resolver el problema seleccionando valores. Pero para mí, se siente más como una adivinación que una solución.
Veamos nuestras cifras de nuevo. En los tres primeros dibujos tenemos dos cuadrados, dos círculos y dos triángulos. Todo esto suma hasta 54. Así que el círculo de media cuadra y el triángulo es 27 (54:2 = 27).

O de otra manera: un círculo más un cuadrado de 10, y un triángulo más un cuadrado de 24, significa un triángulo 14 kilogramos más pesado que un círculo. Es decir, si el círculo se toma como x, entonces el triángulo es x + 14. Luego x + x + 14 = 20; x = 3, y así sucesivamente.
Katya y 4 postales Este problema que encontré en las asignaciones que mi hijo tercer grado tuvo que realizar en las vacaciones de verano. Esto no es la binomy de Newton, pero ¿cómo lo hace sin ecuaciones y sólo métodos elementales de la escuela? ¿Y cuántos niños serán capaces de resolver esto sin un padre que es “fuerte en matemáticas”?
475183.
No puedes hacerlo sin variables otra vez. Supongamos que la primera postal costó un rublos, el segundo - b, el tercero - c, el cuarto - d. Luego b+c+d=42; a+c+d=40; a+b+d=38; a+b+c=36. ¿Qué debemos hacer con esta riqueza?

Está claro que hay que añadir algo, pero no está muy claro qué con qué y por qué motivos. Digamos que armamos todas las partes izquierdas de nuestras expresiones. Consigue 3a+3b+3c+3d o 3(a+d+c+d). Puedes ver que esto es triple el valor de todas las cartas. Desde aquí encontramos su valor (42+40+38+36):3=52 rublos.
Ahora es cuestión de tecnología. 52-42=10 es la primera postal; 52-40=12 es la segunda postal; 52-38=14 es la tercera postal; 52-36=16 es la cuarta postal. Tenga en cuenta que en los comentarios, los adultos inteligentes con dos más altos sugieren “hacer un gráfico lineal simple”, “solver por el método de una calabaza no científica”, “más a menudo acercarse a la tarea, la tarea, dicen, y los huevos no valen la pena. ”

¿Crees que estas tareas ayudan a los estudiantes a desarrollar la lógica o desalentar completamente el deseo de aprender? Es fácil para un adulto, pero ¿pueden explicarlo a un niño? Un niño no decidirá una vez, no decidirá dos veces, y concluirá que nunca será capaz de entender esta terrible matemática. Y la madre suspira y dice: "Qué puedes hacer, mi hijo es un humanitario, no se le da ..."
Cómo el caldo de un pollo comprado difiere del caldo de un pollo doméstico
Perfumes para el verano con el olor del sol y las cabañas que atraerán a los pretendientes sultry