226
Why is there a first grade in school like an institute?
We took these complex mathematical problems from ordinary elementary school textbooks. Parents are outraged and puzzled: “What a mess, how to solve them without X and systems of equations?” ?

It seems that Alla Borisovna knew about this problem back in 1980. Today, first grade is a kind of institution. But unlike the emotional Ph.D. in "First Graduate Songs," we're not going to be over the task of crying. We will try to find simple solutions for them.
Complex mathematical problems Circles, triangles and squares The problem for the first class with an asterisk (increased complexity). It is necessary to find the sum of the circle, triangle and square.
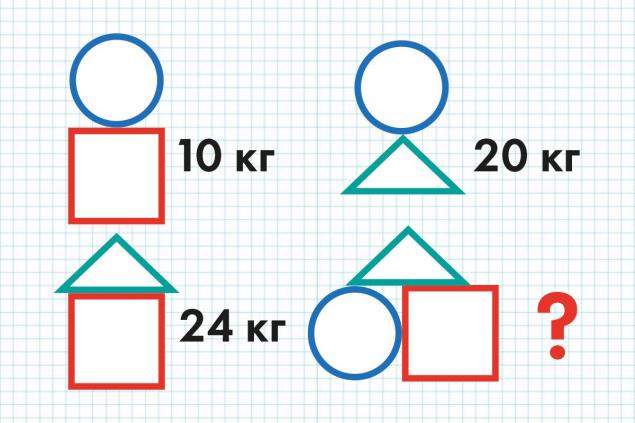
For an adult familiar with algebra, the first impulse is to construct a system of three equations. If the circle is x, the square is y, and the triangle is z, we get:
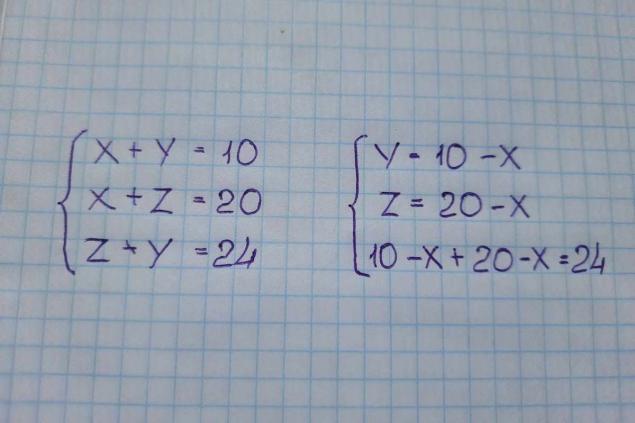
Hence 30 – 2x = 24; 2x = 6; x = 3. The circle (x) is 3, so the square (y) is 7, and the triangle (z) is 17. The sum of the circle, triangle and square gives us 27 kg.
But systems of equations begin to learn only in algebra classes in the 7th grade. Is there a simpler solution? Some parents in the comments suggest solving the problem by selecting values. But to me, it feels more like a divination than a solution.
Let's look at our figures again. In the first three drawings we have two squares, two circles and two triangles. All this adds up to 54. So the half-square circle and triangle is 27 (54:2 = 27).

Or another way: a circle plus a square of 10, and a triangle plus a square of 24, means a triangle 14 kilograms heavier than a circle. That is, if the circle is taken as x, then the triangle is x + 14. Then x + x + 14 = 20; x = 3, and so on.
Katya and 4 postcards This problem I found in the assignments that my son-third grader had to perform on the summer holidays. This is not Newton’s binomy, but how do you do without equations and only elementary school methods? And how many children will be able to solve this without a father who is “strong in mathematics”?

You can't do it without variables again. Suppose that the first postcard cost a rubles, the second - b, the third - c, the fourth - d. Then b+c+d=42; a+c+d=40; a+b+d=38; a+b+c=36. What should we do with this wealth?

It is clear that something needs to be added, but it is not very clear what with what and on what grounds. Let’s say we put together all the left-hand parts of our expressions. You get 3a+3b+3c+3d or 3(a+d+c+d). You can see that this is triple the value of all the cards. From here we find its value (42+40+38+36):3=52 rubles.
Now it's a matter of technology. 52-42=10 is the first postcard; 52-40=12 is the second postcard; 52-38=14 is the third postcard; 52-36=16 is the fourth postcard. Note that in the comments, intelligent adults with two higher ones suggest “draw a simple linear graph”, “solve by the method of an unscientific pumpkin”, “more often approach homework, the task, they say, and eggs are not worth it.”

Do you think that these tasks help students to develop logic or completely discourage the desire to learn? It’s easy for an adult, but can they explain it to a child? A child will not decide once, will not decide two times, and will conclude that he will never be able to understand this terrible mathematics. And the mother sighs and says: "What can you do, my child is a humanitarian, he is not given ..."

It seems that Alla Borisovna knew about this problem back in 1980. Today, first grade is a kind of institution. But unlike the emotional Ph.D. in "First Graduate Songs," we're not going to be over the task of crying. We will try to find simple solutions for them.
Complex mathematical problems Circles, triangles and squares The problem for the first class with an asterisk (increased complexity). It is necessary to find the sum of the circle, triangle and square.

For an adult familiar with algebra, the first impulse is to construct a system of three equations. If the circle is x, the square is y, and the triangle is z, we get:
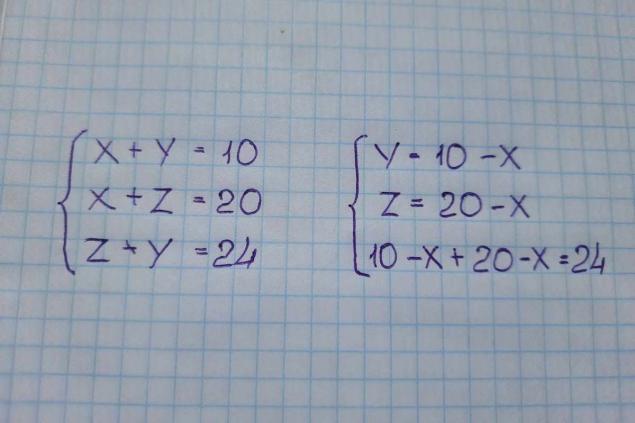
Hence 30 – 2x = 24; 2x = 6; x = 3. The circle (x) is 3, so the square (y) is 7, and the triangle (z) is 17. The sum of the circle, triangle and square gives us 27 kg.
But systems of equations begin to learn only in algebra classes in the 7th grade. Is there a simpler solution? Some parents in the comments suggest solving the problem by selecting values. But to me, it feels more like a divination than a solution.
Let's look at our figures again. In the first three drawings we have two squares, two circles and two triangles. All this adds up to 54. So the half-square circle and triangle is 27 (54:2 = 27).

Or another way: a circle plus a square of 10, and a triangle plus a square of 24, means a triangle 14 kilograms heavier than a circle. That is, if the circle is taken as x, then the triangle is x + 14. Then x + x + 14 = 20; x = 3, and so on.
Katya and 4 postcards This problem I found in the assignments that my son-third grader had to perform on the summer holidays. This is not Newton’s binomy, but how do you do without equations and only elementary school methods? And how many children will be able to solve this without a father who is “strong in mathematics”?

You can't do it without variables again. Suppose that the first postcard cost a rubles, the second - b, the third - c, the fourth - d. Then b+c+d=42; a+c+d=40; a+b+d=38; a+b+c=36. What should we do with this wealth?

It is clear that something needs to be added, but it is not very clear what with what and on what grounds. Let’s say we put together all the left-hand parts of our expressions. You get 3a+3b+3c+3d or 3(a+d+c+d). You can see that this is triple the value of all the cards. From here we find its value (42+40+38+36):3=52 rubles.
Now it's a matter of technology. 52-42=10 is the first postcard; 52-40=12 is the second postcard; 52-38=14 is the third postcard; 52-36=16 is the fourth postcard. Note that in the comments, intelligent adults with two higher ones suggest “draw a simple linear graph”, “solve by the method of an unscientific pumpkin”, “more often approach homework, the task, they say, and eggs are not worth it.”

Do you think that these tasks help students to develop logic or completely discourage the desire to learn? It’s easy for an adult, but can they explain it to a child? A child will not decide once, will not decide two times, and will conclude that he will never be able to understand this terrible mathematics. And the mother sighs and says: "What can you do, my child is a humanitarian, he is not given ..."
How broth from a purchased chicken differs from broth from a domestic chicken
Perfumes for summer with the smell of the sun and cottages that will attract sultry suitors