1296
Paradoja del cumpleaños
Supongamos que usted trabaja en una oficina, que emplea a 23 trabajadores, incluido usted. ¿Cuál es la probabilidad de que dos empleados de la oficina coincidirán los cumpleaños?
(Nosotros no tomamos en cuenta el 29 de febrero)
Su equipo de 23 empleados (que bajo №14):

Respuesta: La probabilidad de que dos personas en la oficina de cumpleaños cae en el mismo día, es de 50%
.
Si el número de personas que llega a 366 dígitos, entonces estadísticamente garantizado que al menos dos personas tienen los cumpleaños coinciden, como tal vez sólo 365 posibles cumpleaños.
Sin embargo, si tenemos en cuenta que todos los cumpleaños son igualmente probables, entonces, para un grupo de 57 personas la probabilidad de que un partido como sería el 99%.

¿Cómo podemos averiguar?
Volvamos a los 23 colegas de la oficina, para entender cómo es esto posible.
Formulamos la inversa:. No hay dos personas en los cumpleaños de los partidos de grupo
Determine la probabilidad de que al menos dos personas en la oficina de celebrar el cumpleaños de un día es muy difícil, si chocan directamente con él.
Determinar la probabilidad de que nadie en el grupo no coinciden con los cumpleaños, mucho más fácil.
La probabilidad de que dos personas no son el mismo cumpleaños, es:
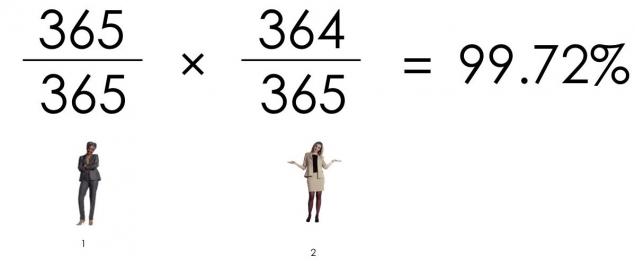
La probabilidad de que tres personas no son el mismo cumpleaños, es:
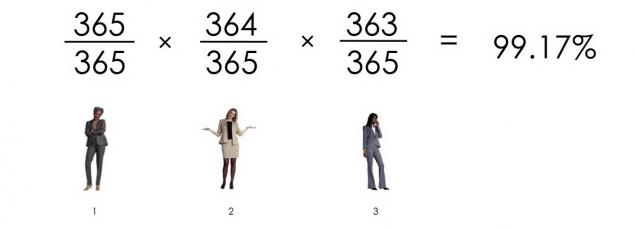
Ver de dónde venimos? La probabilidad de que 23 personas tienen los cumpleaños no coinciden, es:
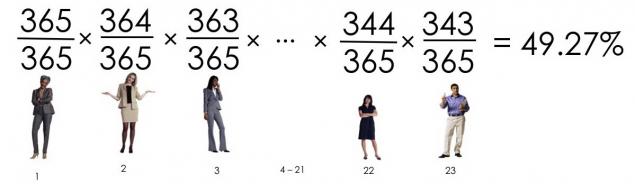
Dado que la probabilidad de que nadie nació en un día fue de 49, 3%, entonces la probabilidad de que al menos dos personas tienen el mismo cumpleaños, es de 50, 7%.
Aquí está la curva de probabilidad:
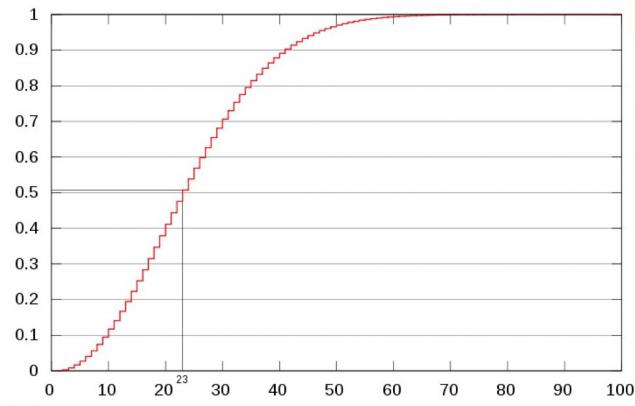
Vertical: la probabilidad de pares; Horizontal: número de personas
(Nosotros no tomamos en cuenta el 29 de febrero)
Su equipo de 23 empleados (que bajo №14):

Respuesta: La probabilidad de que dos personas en la oficina de cumpleaños cae en el mismo día, es de 50%
.
Si el número de personas que llega a 366 dígitos, entonces estadísticamente garantizado que al menos dos personas tienen los cumpleaños coinciden, como tal vez sólo 365 posibles cumpleaños.
Sin embargo, si tenemos en cuenta que todos los cumpleaños son igualmente probables, entonces, para un grupo de 57 personas la probabilidad de que un partido como sería el 99%.

¿Cómo podemos averiguar?
Volvamos a los 23 colegas de la oficina, para entender cómo es esto posible.
Formulamos la inversa:. No hay dos personas en los cumpleaños de los partidos de grupo
Determine la probabilidad de que al menos dos personas en la oficina de celebrar el cumpleaños de un día es muy difícil, si chocan directamente con él.
Determinar la probabilidad de que nadie en el grupo no coinciden con los cumpleaños, mucho más fácil.
La probabilidad de que dos personas no son el mismo cumpleaños, es:
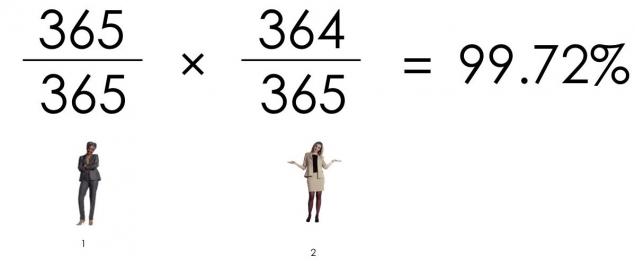
La probabilidad de que tres personas no son el mismo cumpleaños, es:
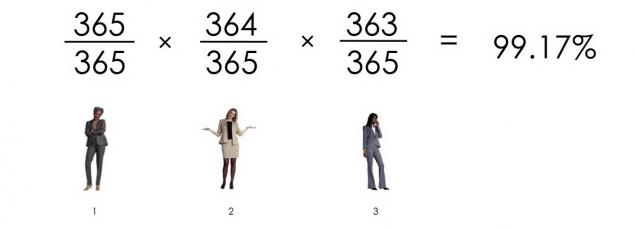
Ver de dónde venimos? La probabilidad de que 23 personas tienen los cumpleaños no coinciden, es:
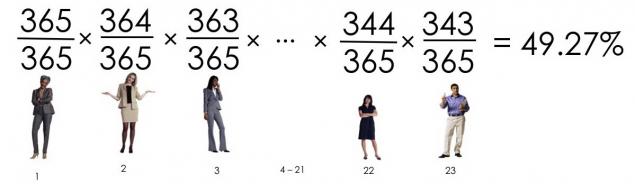
Dado que la probabilidad de que nadie nació en un día fue de 49, 3%, entonces la probabilidad de que al menos dos personas tienen el mismo cumpleaños, es de 50, 7%.
Aquí está la curva de probabilidad:

Vertical: la probabilidad de pares; Horizontal: número de personas