1294
Birthday paradox
Suppose you work in an office, which employs 23 workers, including you. What is the probability that two employees in the office will coincide birthdays?
(We do not take into account the February 29th)
Your team of 23 employees (you under №14):

Answer: The chance that two people in the office birthday falls on the same day, is 50%.
If the number of people reaches 366 digits, then statistically guaranteed that at least two people have birthdays coincide, as perhaps only 365 possible birthdays.
However, if we take into account that all birthdays are equally probable, then, for a group of 57 people the probability of such a match would be 99%.

How can we find out?
Let's go back to the 23 colleagues from the office, to understand how this is possible.
We formulate the converse: no two people in the group match birthdays.
Determine the probability that at least two persons in the office celebrate the birthday of one day is very difficult, if directly collide with it.
Ascertain the likelihood that no one in the group do not match birthdays, much easier.
The probability that two people are not the same birthday, is:
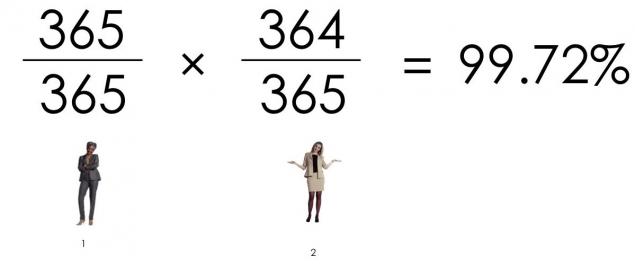
The probability that three people are not the same birthday, is:
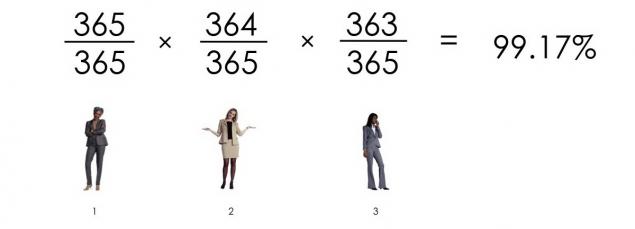
See where we come? The probability that 23 people have birthdays do not match, is:
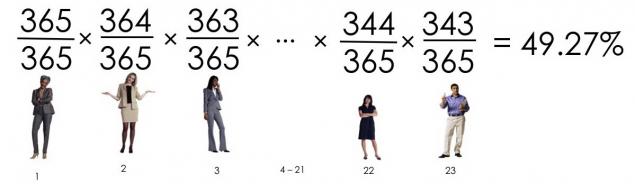
Since the chance that no one was born in one day was 49, 3%, then the chance that at least two people have the same birthday, is 50, 7%.
Here is the probability curve:
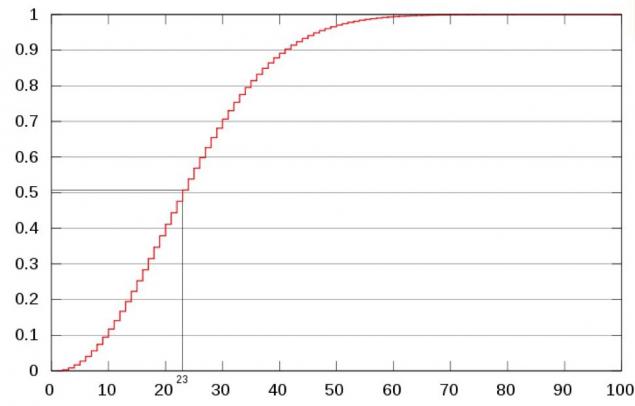
Vertical: the probability of pairs; Horizontal: number of persons
(We do not take into account the February 29th)
Your team of 23 employees (you under №14):

Answer: The chance that two people in the office birthday falls on the same day, is 50%.
If the number of people reaches 366 digits, then statistically guaranteed that at least two people have birthdays coincide, as perhaps only 365 possible birthdays.
However, if we take into account that all birthdays are equally probable, then, for a group of 57 people the probability of such a match would be 99%.

How can we find out?
Let's go back to the 23 colleagues from the office, to understand how this is possible.
We formulate the converse: no two people in the group match birthdays.
Determine the probability that at least two persons in the office celebrate the birthday of one day is very difficult, if directly collide with it.
Ascertain the likelihood that no one in the group do not match birthdays, much easier.
The probability that two people are not the same birthday, is:
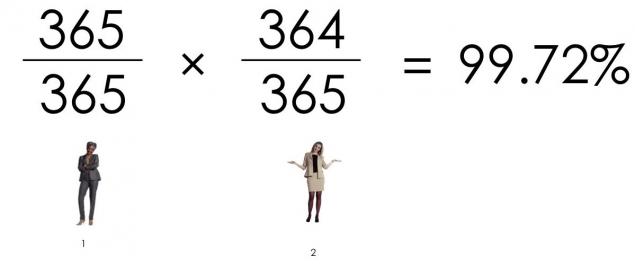
The probability that three people are not the same birthday, is:
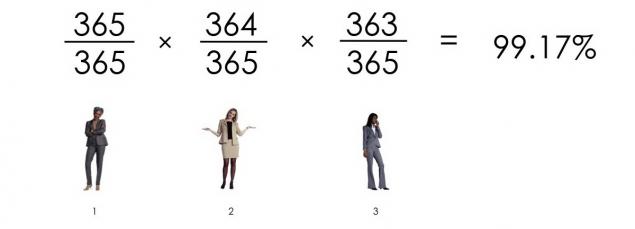
See where we come? The probability that 23 people have birthdays do not match, is:
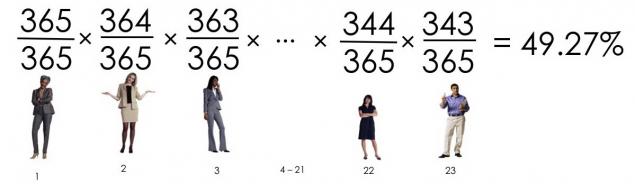
Since the chance that no one was born in one day was 49, 3%, then the chance that at least two people have the same birthday, is 50, 7%.
Here is the probability curve:

Vertical: the probability of pairs; Horizontal: number of persons