1298
Парадокс дня народження
Ви працюєте в офісі з 23 працівниками, включаючи вас. Яка ймовірність того, що два співробітники будуть однакові дні народження?
(Ми не враховуємо 29 лютого)
Ваша команда 23 співробітників (ви маєте номер 14):

Імовірність, що два люди в офісі мають день народження в той же день - 50%.
Якщо кількість людей досягає фігури 366, то статистично гарантовано гарантується, що принаймні два люди будуть мати однаковий день народження, так як можливо тільки 365 ймовірних іменинників.
Однак якщо ви вважаєте, що всі дні народження можуть бути однаково ймовірними, то для групи 57 осіб ймовірність такої збігу становить 99%.

Як дізнатися?
Повернемося до 23 колег в офісі, щоб побачити, як це можливо.
Поперечно, не два люди в групі будуть мати той же день народження.
З'ясуйте ймовірність, що принаймні два люди в офісі святкують День народження в той же день дуже складно, коли стикаються з ним безпосередньо.
З'ясуйте ймовірність, що ніхто не в групі має такий же день народження набагато простіше.
Імовірність того, що два люди не мають такого ж дня:
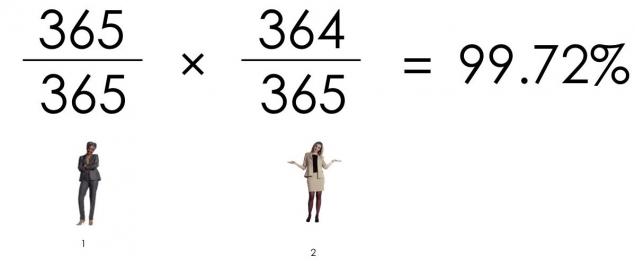
Імовірність, що три люди не мають такого ж дня:
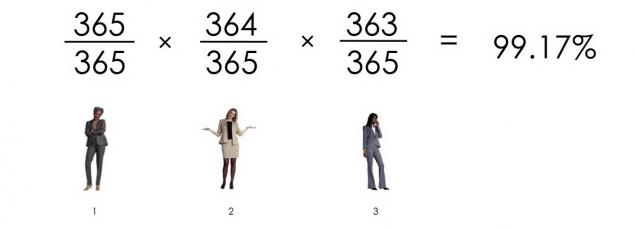
Що ми отримуємо? Імовірність, що 23 людей мають різні дні народження:
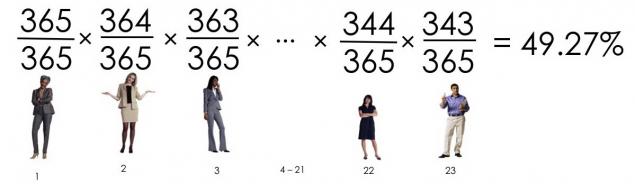
З шансу, що ніхто не народився на той же день, 49,3%, ймовірність, що принаймні два люди мають однаковий день народження 50,7%.
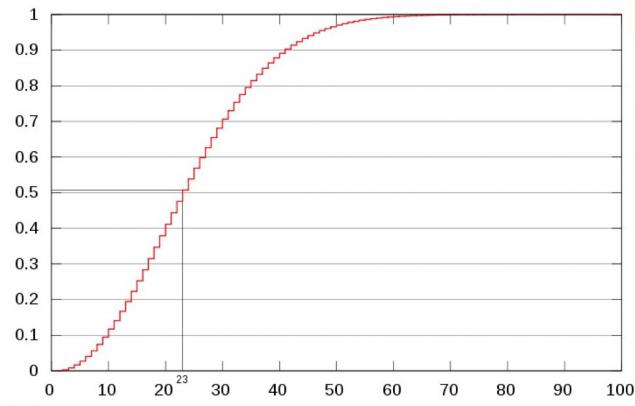
Ось чого виглядає крива ймовірність:
 р.
р.
Вертикалізація: ймовірність пар; горизонтальна: кількість людей
(Ми не враховуємо 29 лютого)
Ваша команда 23 співробітників (ви маєте номер 14):

Імовірність, що два люди в офісі мають день народження в той же день - 50%.
Якщо кількість людей досягає фігури 366, то статистично гарантовано гарантується, що принаймні два люди будуть мати однаковий день народження, так як можливо тільки 365 ймовірних іменинників.
Однак якщо ви вважаєте, що всі дні народження можуть бути однаково ймовірними, то для групи 57 осіб ймовірність такої збігу становить 99%.

Як дізнатися?
Повернемося до 23 колег в офісі, щоб побачити, як це можливо.
Поперечно, не два люди в групі будуть мати той же день народження.
З'ясуйте ймовірність, що принаймні два люди в офісі святкують День народження в той же день дуже складно, коли стикаються з ним безпосередньо.
З'ясуйте ймовірність, що ніхто не в групі має такий же день народження набагато простіше.
Імовірність того, що два люди не мають такого ж дня:
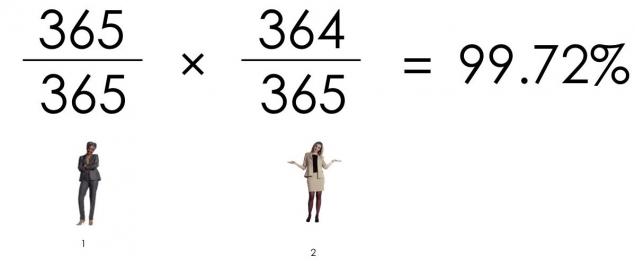
Імовірність, що три люди не мають такого ж дня:
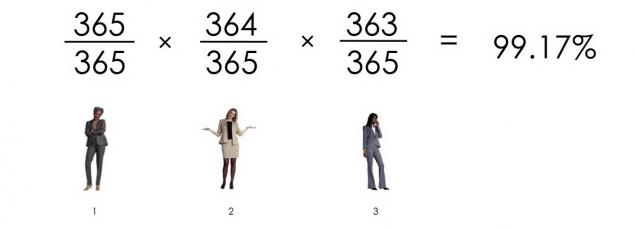
Що ми отримуємо? Імовірність, що 23 людей мають різні дні народження:
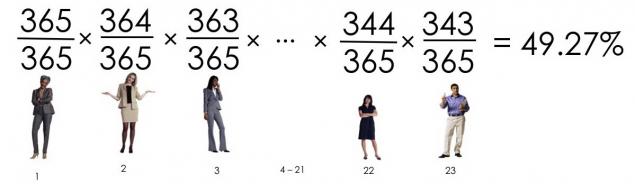
З шансу, що ніхто не народився на той же день, 49,3%, ймовірність, що принаймні два люди мають однаковий день народження 50,7%.
Ось чого виглядає крива ймовірність:
 р.
р.Вертикалізація: ймовірність пар; горизонтальна: кількість людей