1296
生日悖论
假设你在办公室,拥有员工23名,其中包括你的工作。什么是两名员工在办公室将一致生日的概率是多少?
(我们不考虑在2月29日)
你的23名员工(你在№14)团队:

答:有两个人在办公室的生日在同一天,机会是50%
。
如果人数达到366位,从统计学保证至少有两个人生日相吻合,因为也许只有365可能的生日。
但是,如果我们考虑到所有的生日是同样可能的话,一组57人的这样的比赛的概率是99%。

我们怎样才能找到?
让我们回到23同事的办公室,以了解这是可能的。
我们制定了相反:没有两个人在小组赛中生日
确定在办公室里至少有两个人庆祝一天的生日是非常困难的,如果直接与它发生碰撞的概率。
确定的可能性,没有人组中不匹配的生日,要容易得多。
两个人是不一样的生日的概率是:
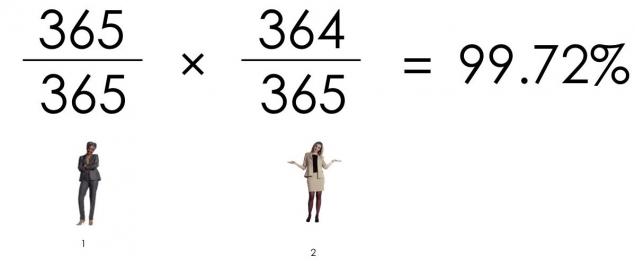
这三个人都不是同一天生日的概率是:
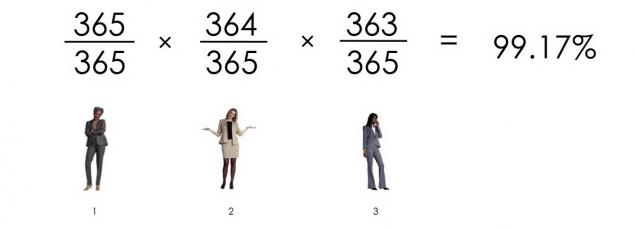
看到我们来了?这23人有生日不匹配的概率是:
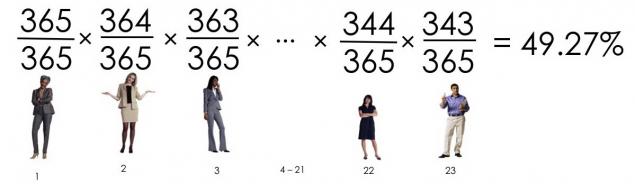
既然没有人出生在一天为49,3%,那么机会,至少有两个人有相同的生日,50,7%的机会。
这里是概率曲线:
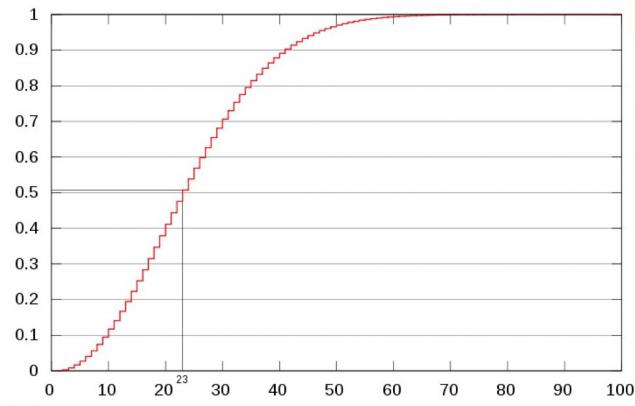
垂直:对的概率;水平:人数
(我们不考虑在2月29日)
你的23名员工(你在№14)团队:

答:有两个人在办公室的生日在同一天,机会是50%
。
如果人数达到366位,从统计学保证至少有两个人生日相吻合,因为也许只有365可能的生日。
但是,如果我们考虑到所有的生日是同样可能的话,一组57人的这样的比赛的概率是99%。

我们怎样才能找到?
让我们回到23同事的办公室,以了解这是可能的。
我们制定了相反:没有两个人在小组赛中生日
确定在办公室里至少有两个人庆祝一天的生日是非常困难的,如果直接与它发生碰撞的概率。
确定的可能性,没有人组中不匹配的生日,要容易得多。
两个人是不一样的生日的概率是:
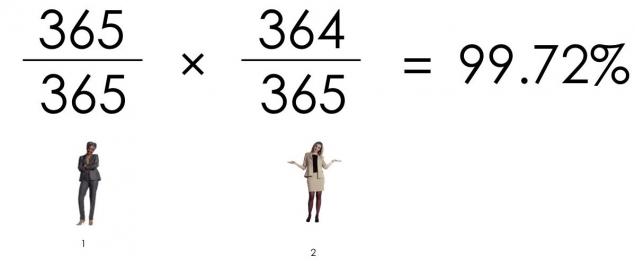
这三个人都不是同一天生日的概率是:
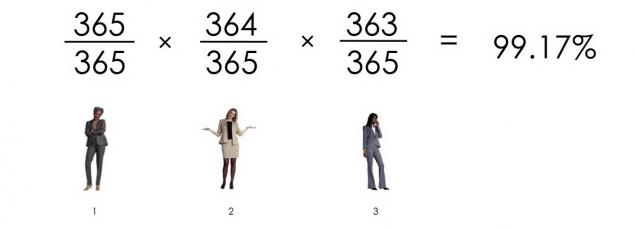
看到我们来了?这23人有生日不匹配的概率是:
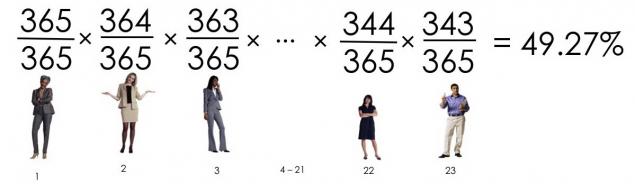
既然没有人出生在一天为49,3%,那么机会,至少有两个人有相同的生日,50,7%的机会。
这里是概率曲线:

垂直:对的概率;水平:人数