606
蒙提霍尔问题
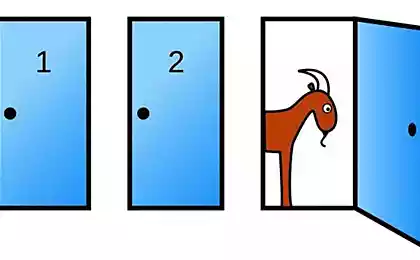
想象一下,一个银行家提供您选择三个封闭的箱子之一。在其中一次50美分,在其他 - 美元在第三 - 万把块钱。什么选择,而你会得到一个奖。
您可以选择随机,说,一箱№1。然后银行家(当然是谁,知道哪里是)在你的眼前打开了一美元(说它№2)一箱,然后提供改变原先选定的板对板№1№3。
如果你改变你的决定吗?这是否会增加,当你获得10000的机会?
这是蒙提霍尔问题 - 概率论的问题,其中的解决方案,乍看之下,有悖常理。在这个任务的人摸不着头脑,因为1975年
吊诡的是为了纪念著名的美国电视节目主持人名叫«让我们做个交易»。在这个电视节目也有类似的规则,只有参与者选择了门后,他们两个人躲在山羊,第三个 - 凯迪拉克
维基

大多数玩家推测,两人离开了紧闭的大门,其中一个是凯迪拉克,得到50-50.Ochevidno当领导打开一扇门,并提供改变主意的机会后,他开始一个新游戏。改变的解决方案,否则将无法改变,你的胜算仍然等于50%。所以毕竟?
事实证明,有。事实上,改变的决定,你双击你成功的机会。为什么呢?
领导知道该奖项的位置。他可以不开门,你所选择的一个是其中有一个奖(您喜欢山羊的选择,而不是凯迪拉克,我们不考虑)。
你有两个选择 - 留在他或更改的决定。比方说,你决定不改变任何东西。然后,机器你得到的,除非你真的只是猜测正确的门。如果你已经改变了决定,那么你就赢了,如果你一开始走错了门。
按照这个逻辑,如果你留在他们的选择,你的机会是平等的1/3,如果你改变你的决定 - 2/3
令人惊奇的是,不是每个两种选择是第五十50的成功的可能性。
在1990年这个问题及其解决方案已发表在美国杂志“巡游”。出版引起了读者的愤怒的评论,其中许多人有学位的混乱。
主要的抱怨是没有问题的所有条件已经规定,任何细微差别可能会影响结果。例如,前沿变化可以提供一个解决方案仅如果玩家选择的车辆的第一场。很明显,在这种情况下的初始选择的变化将导致保证失败。
然而,在电视节目蒙提霍尔人们改变决定,还赢的次数两倍的存在:
在30名球员谁改变了最初的决定,凯迪拉克荣获18 - 即60%
在30名球员谁留在自己选择的,凯迪拉克荣获11 - 或约36%
因此,在决定中给出的理由,但是非理性的,他们似乎,被实践所证实。

资料来源:
您可以选择随机,说,一箱№1。然后银行家(当然是谁,知道哪里是)在你的眼前打开了一美元(说它№2)一箱,然后提供改变原先选定的板对板№1№3。
如果你改变你的决定吗?这是否会增加,当你获得10000的机会?
这是蒙提霍尔问题 - 概率论的问题,其中的解决方案,乍看之下,有悖常理。在这个任务的人摸不着头脑,因为1975年
吊诡的是为了纪念著名的美国电视节目主持人名叫«让我们做个交易»。在这个电视节目也有类似的规则,只有参与者选择了门后,他们两个人躲在山羊,第三个 - 凯迪拉克
维基

大多数玩家推测,两人离开了紧闭的大门,其中一个是凯迪拉克,得到50-50.Ochevidno当领导打开一扇门,并提供改变主意的机会后,他开始一个新游戏。改变的解决方案,否则将无法改变,你的胜算仍然等于50%。所以毕竟?
事实证明,有。事实上,改变的决定,你双击你成功的机会。为什么呢?
领导知道该奖项的位置。他可以不开门,你所选择的一个是其中有一个奖(您喜欢山羊的选择,而不是凯迪拉克,我们不考虑)。
你有两个选择 - 留在他或更改的决定。比方说,你决定不改变任何东西。然后,机器你得到的,除非你真的只是猜测正确的门。如果你已经改变了决定,那么你就赢了,如果你一开始走错了门。
按照这个逻辑,如果你留在他们的选择,你的机会是平等的1/3,如果你改变你的决定 - 2/3
令人惊奇的是,不是每个两种选择是第五十50的成功的可能性。
在1990年这个问题及其解决方案已发表在美国杂志“巡游”。出版引起了读者的愤怒的评论,其中许多人有学位的混乱。
主要的抱怨是没有问题的所有条件已经规定,任何细微差别可能会影响结果。例如,前沿变化可以提供一个解决方案仅如果玩家选择的车辆的第一场。很明显,在这种情况下的初始选择的变化将导致保证失败。
然而,在电视节目蒙提霍尔人们改变决定,还赢的次数两倍的存在:
在30名球员谁改变了最初的决定,凯迪拉克荣获18 - 即60%
在30名球员谁留在自己选择的,凯迪拉克荣获11 - 或约36%
因此,在决定中给出的理由,但是非理性的,他们似乎,被实践所证实。

资料来源: