603
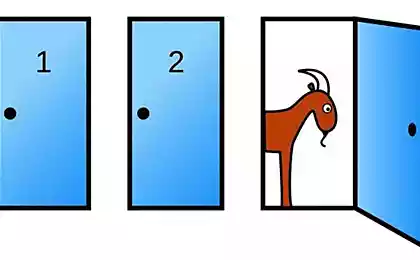
Monty Hall Problem
Imagine that a banker offers you to select one of three closed boxes. In one of them 50 cents, in the other - a dollar in the third - 10 thousand dollars. What choose, and that you will get a prize.
You choose at random, say, a box №1. Then the banker (who, of course, knows where that) right before your eyes opens a box with a one dollar (say it №2), and then offers to change the originally selected box to box №1 №3.
Should you change your decision? Whether this will increase when your chances of getting 10 thousand?
This is Monty Hall Problem - the problem of probability theory, the solution of which, at first glance, counterintuitive. On this task people scratching their heads since 1975.
The paradox was named in honor of the popular American television show host «Let's Make a Deal». In this TV show had similar rules, only the participants chose the door behind the two of them were hiding goats, for the third - Cadillac.
Wiki

Most of the players speculated that after the two left the closed doors and one of them is the Cadillac, the chances to get 50-50.Ochevidno that when the lead opens one door and offers to change his mind, he starts a new game. Change the solution or you will not change, your odds will still be equal to 50 percent. So after all?
It turns out that there is. In fact, changing decision, you double your chances of success. Why?
Leading knows the location of the prize. He could not open the door, which you have chosen and the one for which there is a prize (the option that you prefer a goat, not a Cadillac, we do not consider).
You have two choices - to stay at his or change a decision. Let's say you decide not to change anything. Then the machine you get, unless you're really just guessing the correct door. If you have changed the decision, then you win, if you initially mistaken the door.
According to this logic, if you stay at their choice, your chances are equal to 1/3, and if you change your decision - 2/3.
Surprisingly, not every two choices is the likelihood of success of Fifty-fifty.
In 1990 this problem and its solution have been published in the American journal "Parade". The publication caused a flurry of indignant comments of readers, many of whom had academic degrees.
The main complaint was that not all the conditions of the problem have been stipulated, and any nuance could affect the outcome. For example, the leading change could offer a solution only if the player chose the first course of the vehicle. It is obvious that a change in the initial choice of such a situation will lead to the guaranteed defeat.
However, during the existence of the TV show Monty Hall People changing decision did win twice as often:
Of the 30 players who changed the initial decision, Cadillac won 18 - ie 60%
Of the 30 players who remain at their choice, Cadillac won 11 - or about 36%
So the reasoning given in the decision, however irrational they may seem, are confirmed by the practice.

Source:
You choose at random, say, a box №1. Then the banker (who, of course, knows where that) right before your eyes opens a box with a one dollar (say it №2), and then offers to change the originally selected box to box №1 №3.
Should you change your decision? Whether this will increase when your chances of getting 10 thousand?
This is Monty Hall Problem - the problem of probability theory, the solution of which, at first glance, counterintuitive. On this task people scratching their heads since 1975.
The paradox was named in honor of the popular American television show host «Let's Make a Deal». In this TV show had similar rules, only the participants chose the door behind the two of them were hiding goats, for the third - Cadillac.
Wiki

Most of the players speculated that after the two left the closed doors and one of them is the Cadillac, the chances to get 50-50.Ochevidno that when the lead opens one door and offers to change his mind, he starts a new game. Change the solution or you will not change, your odds will still be equal to 50 percent. So after all?
It turns out that there is. In fact, changing decision, you double your chances of success. Why?
Leading knows the location of the prize. He could not open the door, which you have chosen and the one for which there is a prize (the option that you prefer a goat, not a Cadillac, we do not consider).
You have two choices - to stay at his or change a decision. Let's say you decide not to change anything. Then the machine you get, unless you're really just guessing the correct door. If you have changed the decision, then you win, if you initially mistaken the door.
According to this logic, if you stay at their choice, your chances are equal to 1/3, and if you change your decision - 2/3.
Surprisingly, not every two choices is the likelihood of success of Fifty-fifty.
In 1990 this problem and its solution have been published in the American journal "Parade". The publication caused a flurry of indignant comments of readers, many of whom had academic degrees.
The main complaint was that not all the conditions of the problem have been stipulated, and any nuance could affect the outcome. For example, the leading change could offer a solution only if the player chose the first course of the vehicle. It is obvious that a change in the initial choice of such a situation will lead to the guaranteed defeat.
However, during the existence of the TV show Monty Hall People changing decision did win twice as often:
Of the 30 players who changed the initial decision, Cadillac won 18 - ie 60%
Of the 30 players who remain at their choice, Cadillac won 11 - or about 36%
So the reasoning given in the decision, however irrational they may seem, are confirmed by the practice.

Source: