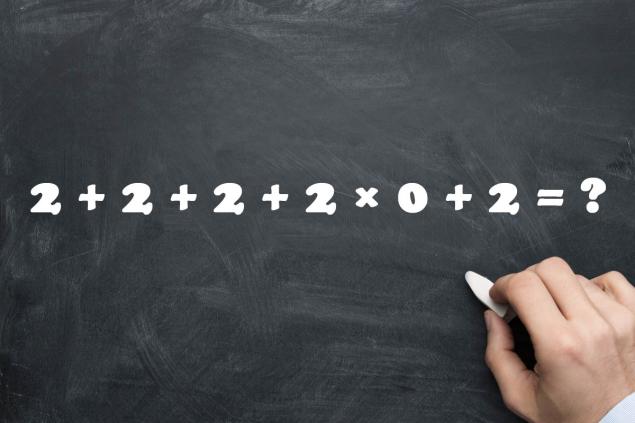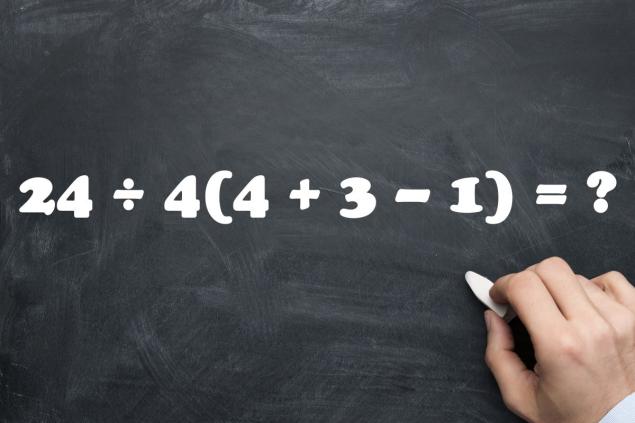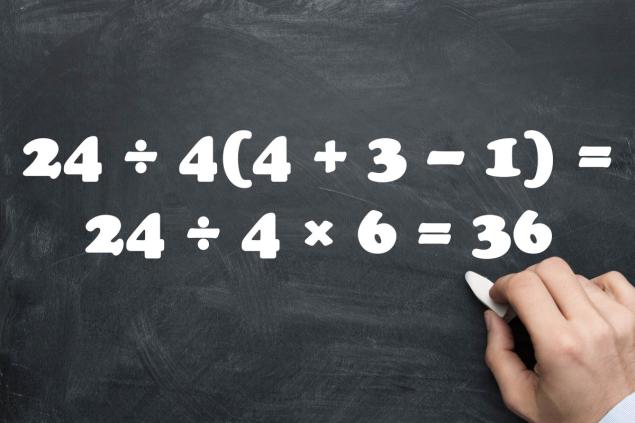Стівен Говерлінг зробить вас пересуватися, але вирішуйте без калькулятора

Приклади дії Що кожен студент проводить більше десятків годин. Однак, після успішного проходження випробувань і іспитів, всі придбані знання погодні з відлякуванням швидкості. І здавалося б, що так багато роботи інвестували в дослідження, але незабаром не існує слідів всіх цих мудростей.

Сьогодні видання. "Сайт" Пропонуємо перевірити, наскільки добре ви опанували основні алгоритми розв’язання прикладів. Серед інших речей, навіть є приклад атрибутів легендарного англійського вченого Стівена Гокінга.



Приклади дії

1. Перший приклад, ймовірно, буде прийнятий багатьма. Якщо ви знаєте всі необхідні правила, то ви обов'язково не будете плутати в цій кількості двох. Незважаючи на те, що багатозастосувань від нуля можна заплутати всі карти. Будьте обережні з кожною арифметичною роботою.
   
   
   
   
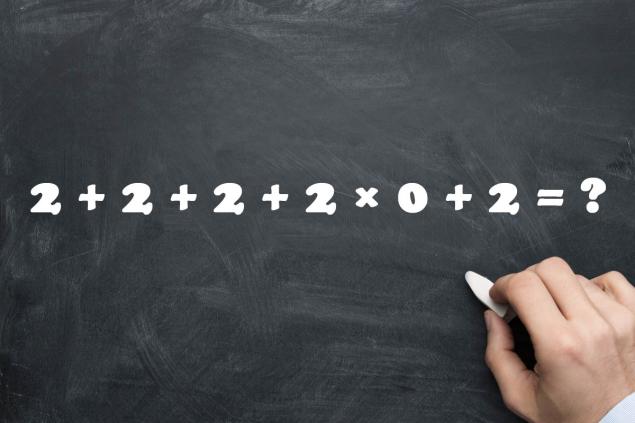
2. У другому математичному прикладі, крім додавання і багатозастосувань, вам також доведеться розділити. Це не збирається бути великою проблемою для вас. На жаль, намагатися вирішити без помилок, запам'ятовуючи по дорозі ті правила, які часто повторюються суворим математиком.
   
   
   
   
3. Останній приклад (і його різні варіації) зараховується до Стівена Гокінга. Тексти пісень, а це означає: І дійсно є щось блискуче про це. Після того, як все інше, щоб пояснити, що завжди є нагрітими дебатами. І кожен читач впевнений, що його рішення прикладу правильно. Правильна відповідь, звичайно, є тільки одним.
   
   
   
   

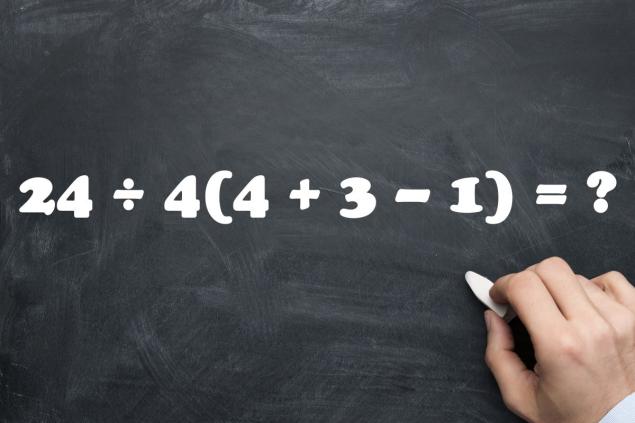
Поради та рішення

1. Багато людей обирають тут (як приклад, так і як оцінка), так як всі арифметичні операції виконуються строго послідовно зліво направо. Але реальні студенти старших шкіл знають, що багатозастосування зроблено тут першим, не додавання. до 1 2 3 4 5+
   
   
   
   
2. Золоте правило «перше виконання поділу і багатозастосувань, а потім додавання і відступ» корисно у вирішенні другого прикладу. 5 + 5 ÷ 5 + 3 × 3 = 5 + 1 + 9 = 15.
   
   
   
   
3. Ось, перш за все, вам доведеться виконувати дії в дужках. А потім, коли дужки відкриті, ходять строго зліва направо. І в цьому випадку ми отримуємо: 24 ÷ 4(4 + 3 - 1) = 24 ÷ 4 × 6 = 36. Багато людей отримують один, але це відповідь неправильно.
   
   
   
   

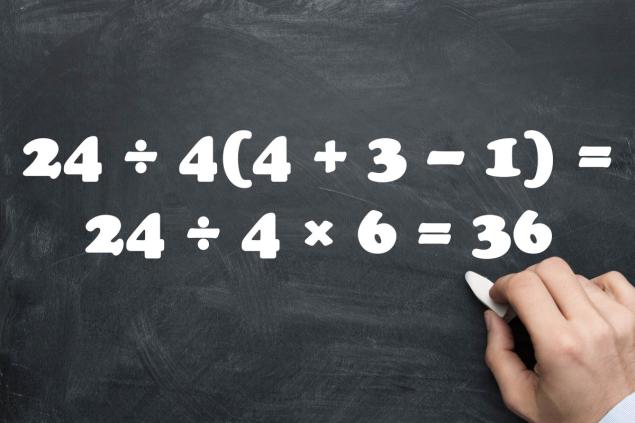
Не забудьте написати відповіді, які ви отримали, і чи відповідаєте нам наші. Також вирішуйте складні приклади. Або подивіться на рішення для цікавих головоломок, які ми опублікували нещодавно. Таке тепло для розуму обов'язково буде корисним.