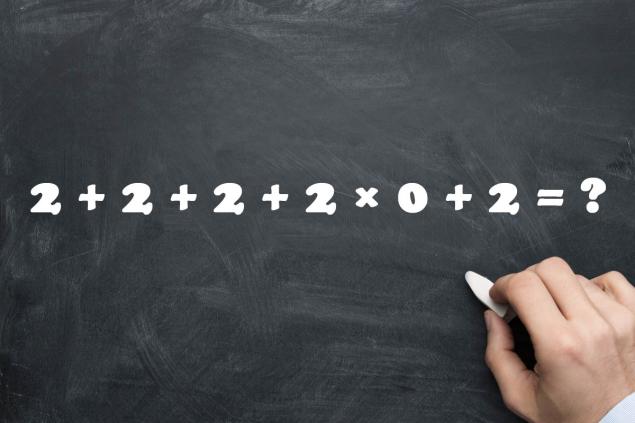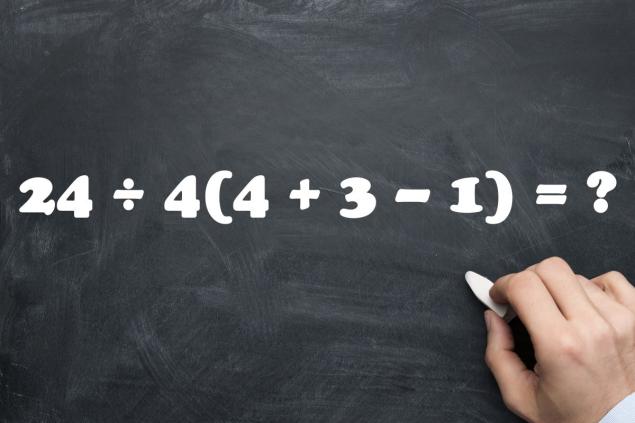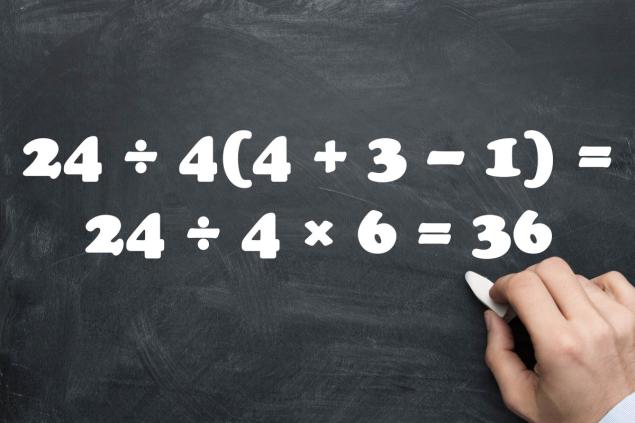Stephen Hawking te hará mover las convoluciones, pero decide sin la calculadora

Tomando ejemplos de medidas Lo que cada estudiante pasa más de una docena de horas. Sin embargo, después de haber aprobado con éxito las pruebas y exámenes, todo conocimiento adquirido está climatizado con una velocidad aterradora. Y parecería que tanto trabajo se ha invertido en el estudio, pero pronto no hay rastro de todas estas sabidurías.

La edición de hoy. "Site" Ofrece comprobar lo bien que dominaste los algoritmos básicos para resolver ejemplos. Entre otras cosas, incluso habrá un ejemplo atribuido al legendario científico inglés Stephen Hawking.



Tomando ejemplos de medidas

1. Es probable que muchos tomen el primer ejemplo. Si usted conoce todas las reglas necesarias, entonces definitivamente no se confundirá en esta abundancia de dos. Aunque la multiplicación por cero puede confundir todas las tarjetas. Ten cuidado con cada operación aritmética.
   
   
   
   
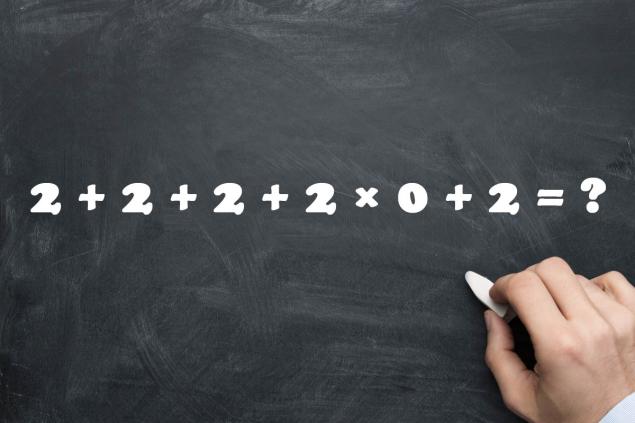
2. En el segundo ejemplo matemático, además de la adición y la multiplicación, también tiene que dividir. No va a ser un gran problema para ti. Sin embargo, trate de resolver sin errores, recordando las reglas que a menudo fueron repetidas por un matemático estricto.
   
   
   
   
3. Este último ejemplo (y sus diversas variaciones) se atribuye al propio Stephen Hawking. Y realmente hay algo brillante en ello. Después de todo, ¿cómo explicar que siempre hay un debate acalorado en torno a este ejemplo? Y cada lector está seguro de que su decisión del ejemplo es correcta. La respuesta correcta, por supuesto, es sólo una.
   
   
   
   

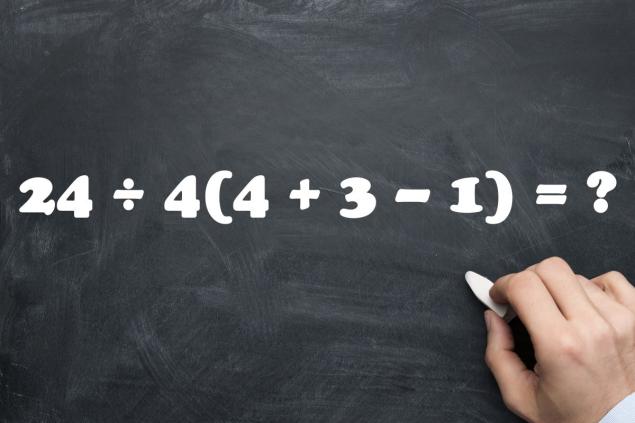
Consejos y soluciones

1. Muchas personas obtienen un deuce aquí (ambos como ejemplo y como estimación), ya que todas las operaciones aritméticas se realizan estrictamente secuencialmente de izquierda a derecha. Pero los estudiantes de secundaria saben que la multiplicación se hace aquí primero, no la adición. 2 + 2 + 2 + 2 × 0 + 2 = 2 + 2 + 2 + 0 + 2 = 8
   
   
   
   
2. La regla de oro “primero realiza división y multiplicación, y luego adición y resta” es útil para resolver el segundo ejemplo. Luego 5 + 5 ÷ 5 + 3 × 3 = 5 + 1 + 9 = 15.
   
   
   
   
3. Aquí, en primer lugar, tendrá que realizar acciones entre corchetes. Y luego, cuando los corchetes estén abiertos, vaya estrictamente de izquierda a derecha. Y en este caso obtenemos: 24 ÷ 4(4 + 3 - 1) = 24 ÷ 4 × 6 = 36. Muchas personas reciben uno, pero esta respuesta es incorrecta.
   
   
   
   

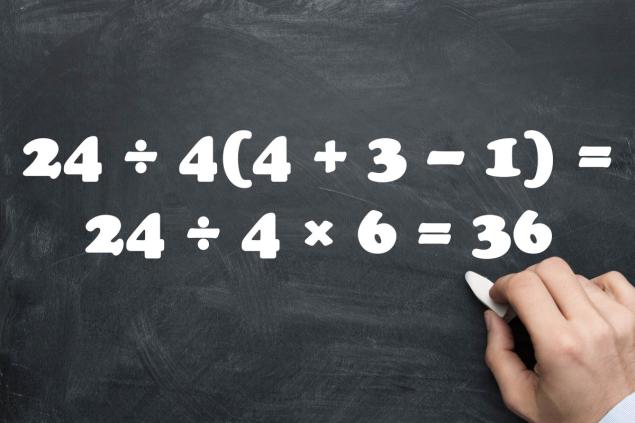
No olvides escribir las respuestas que tienes y si coinciden con las nuestras. También resolver nuestros ejemplos más complejos. O busque soluciones a los curiosos puzzles que publicamos recientemente. Tal calentamiento para la mente definitivamente será útil.