1036
Фібоначчі числа
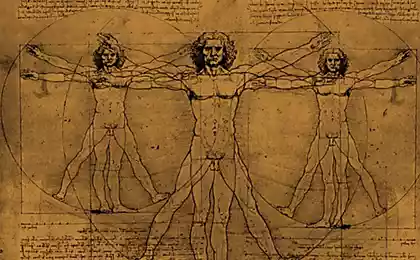
Фібоначчі є одним з найбільших європейських середньовічних математик перших величин.
Його роботи включили найцінніші знання в галузі математики цього часу.
Він перевершив знання кращих вчених своєї ери, перед ними майже дві сотні років.
закладання основи розвитку науки в Західній Європі на основі математичного
знання Араб і індуси.
У 1200 році Леонардо повернувся до Писа і почав писати його першу книгу, книгу Абаку.
У своїй книзі Фібоначчі сильно підтримали індійські методи розрахунку.
За словами історика математики А. П. Юшкевича, «Книжка Абаки» різко зростає над європейським.
арифметична-альгебраїчна література XII-XIV ст за різноманітністю і міцністю методів,
багатість завдань, доказ презентації ... Наслідки математиків звернулися з неї.
як завдання, так і методи їх вирішення. Багато поколінь європейських математиків
Вивчаємо індійську послідовну систему.
У розділі XII наведено завдання щодо підсумування серії - арифметичне та геометричне прогресування,
серія квадратів і, вперше в історії математики, серія повернення веде до послідовності
Так звані номери Фібоначчі.

Фібоначчі числа - елементи послідовності рядів
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, ...
Кожна наступна кількість дорівнює сумі двох передових чисел.
(Сімейний номер 0 не вважається членом послідовності)
3+2=5.5+3=8.8+5=13.13+8=21 та ін.
І точка цих чисел є те, що практично все в нашому світі побудовано на цій чисельній послідовності.
Все на землі! Навіть наш Всесвіт складається з цих чисел.
Це величезна і неймовірна таємничість людства!

Але найдивовижніше про цифри Fibonacci це не так.
Якщо ви будуєте прямокутник з рівних сторін
дві суміжні номери і розділіть його на багато маленьких прямокутників
Кожен з них дорівнює кількості
А потім покладіть дугу в прямокутників.
Ми будемо бачити бездоганну кручену спіраль.
Парадоксально це у вигляді такої спіралі, яка так багато була створена в нашому світі:
 р.
р.
Зрозуміло навіть мікроскопічні відбитки пальців наших пальців.
Великі галактики мають однаковий візерунок!
Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз.

Його роботи включили найцінніші знання в галузі математики цього часу.
Він перевершив знання кращих вчених своєї ери, перед ними майже дві сотні років.
закладання основи розвитку науки в Західній Європі на основі математичного
знання Араб і індуси.
У 1200 році Леонардо повернувся до Писа і почав писати його першу книгу, книгу Абаку.
У своїй книзі Фібоначчі сильно підтримали індійські методи розрахунку.
За словами історика математики А. П. Юшкевича, «Книжка Абаки» різко зростає над європейським.
арифметична-альгебраїчна література XII-XIV ст за різноманітністю і міцністю методів,
багатість завдань, доказ презентації ... Наслідки математиків звернулися з неї.
як завдання, так і методи їх вирішення. Багато поколінь європейських математиків
Вивчаємо індійську послідовну систему.
У розділі XII наведено завдання щодо підсумування серії - арифметичне та геометричне прогресування,
серія квадратів і, вперше в історії математики, серія повернення веде до послідовності
Так звані номери Фібоначчі.

Фібоначчі числа - елементи послідовності рядів
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, ...
Кожна наступна кількість дорівнює сумі двох передових чисел.
(Сімейний номер 0 не вважається членом послідовності)
3+2=5.5+3=8.8+5=13.13+8=21 та ін.
І точка цих чисел є те, що практично все в нашому світі побудовано на цій чисельній послідовності.
Все на землі! Навіть наш Всесвіт складається з цих чисел.
Це величезна і неймовірна таємничість людства!

Але найдивовижніше про цифри Fibonacci це не так.
Якщо ви будуєте прямокутник з рівних сторін
дві суміжні номери і розділіть його на багато маленьких прямокутників
Кожен з них дорівнює кількості
А потім покладіть дугу в прямокутників.
Ми будемо бачити бездоганну кручену спіраль.
Парадоксально це у вигляді такої спіралі, яка так багато була створена в нашому світі:
 р.
р.Зрозуміло навіть мікроскопічні відбитки пальців наших пальців.
Великі галактики мають однаковий візерунок!
Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз.