159
La tortura mental de un tercer grado de Kazajstán, ¿puedes decidir?
Mi profesor favorito de matemáticas, Peter Zemskov, sigue lanzando comida para nuestras mentes. Recientemente, en su canal de YouTube, ofreció suscriptores. resolver el problema de la tercera clase. ¿Parece que puede ser difícil? ¡Esa es la belleza!

Los escolares hacen clic en estos problemas como nueces. Los adultos, por otro lado, tienen que trabajar duro para encontrar la respuesta correcta. Me pregunto si puedes hacerlo.
En primer lugar, sugiero que mires el problema que tenemos que resolver hoy. Piense en dónde empezar y cómo mejor abordar un ejemplo de una manera que lo hace el más rápido. Y luego te diré cómo lo decidió el profesor de matemáticas.

Peter Zemskov es un profesor de matemáticas experimentado. Así que cuando su sobrino de Kazajstán lo llamó y se ofreció a resolver el problema de la tercera clase, el hombre respondió inmediatamente. El único problema es que empezó a decidir como adulto.
Zemskov determinó que hay tres variables en el ejemplo. Nos detenemos ahora mismo. ¿Por qué tres en lugar de cuatro? ¡Es simple! Dos de los cuatro ejemplos dan lugar a 8. Al número que está en la plaza superior derecha, necesita añadir el mismo número para obtener 8.

Este conocimiento ayudó Peter para componer el sistema y presentar las variables desconocidas como sigue: + y = 8, + z = 13, z - = 6. Y en esta etapa, el matemático se dio cuenta de que los tercer grado todavía no saben cómo resolver tales ecuaciones. Debe haber una manera más simple y más accesible.
Llamada telefónica. Al otro extremo del alambre, la voz de un niño suena: “Todavía no hemos aprendido fracciones”. ¡Pero enseñamos la mitad! Aquí está la respuesta a todas las preguntas. Zemskov vuelve a resolver el problema de la tercera clase y piensa como un estudiante debe pensar.
El maestro aborda el problema a través del juego: “Si las escalas están en equilibrio, entonces las escalas pueden ser agregadas.” Es lo mismo con la igualdad. Podemos doblarlos juntos a la izquierda y a la derecha”. Peter sugiere añadir un ejemplo con respuesta 13 y un ejemplo con respuesta 6. Recuerde que 2 de estos ejemplos son los mismos.

Como vemos la adición en el primer ejemplo (con la respuesta 13) y la resta en el segundo ejemplo, los mismos números simplemente desaparecen cuando se añade. El único número desconocido se añade dos veces. "Dos cubos como este son trece más seis", explica el maestro, señalando a la plaza en la esquina inferior izquierda. 13 + 6 = 19, y 19 ÷ 2 = 9,5.

Y entonces todo se resuelve muy simplemente. Sustituir 9.5 en el lugar correcto y calcular cuánto necesita para restar de este número para obtener 6. La acción es simple, así que ni siquiera necesitamos grabarla.
El resultado es: 9.5 - 3.5 = 6. Recuerde que los números en el cuadrado inferior derecho y superior izquierdo son los mismos. Queda por descubrir lo que hay en la última plaza. Aquí vamos. 3.5 + 4.5 = 8.
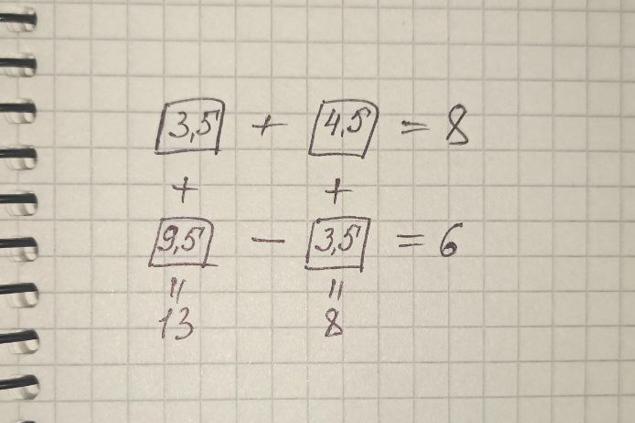
Dime, ¿te las arreglaste para resolver este problema? Por cierto, sería genial si pusieras un ejemplo para tus hijos. Comparte en los comentarios si lograron hacer frente a ella. ¡Espérate abajo!

Los escolares hacen clic en estos problemas como nueces. Los adultos, por otro lado, tienen que trabajar duro para encontrar la respuesta correcta. Me pregunto si puedes hacerlo.
En primer lugar, sugiero que mires el problema que tenemos que resolver hoy. Piense en dónde empezar y cómo mejor abordar un ejemplo de una manera que lo hace el más rápido. Y luego te diré cómo lo decidió el profesor de matemáticas.

Peter Zemskov es un profesor de matemáticas experimentado. Así que cuando su sobrino de Kazajstán lo llamó y se ofreció a resolver el problema de la tercera clase, el hombre respondió inmediatamente. El único problema es que empezó a decidir como adulto.
Zemskov determinó que hay tres variables en el ejemplo. Nos detenemos ahora mismo. ¿Por qué tres en lugar de cuatro? ¡Es simple! Dos de los cuatro ejemplos dan lugar a 8. Al número que está en la plaza superior derecha, necesita añadir el mismo número para obtener 8.

Este conocimiento ayudó Peter para componer el sistema y presentar las variables desconocidas como sigue: + y = 8, + z = 13, z - = 6. Y en esta etapa, el matemático se dio cuenta de que los tercer grado todavía no saben cómo resolver tales ecuaciones. Debe haber una manera más simple y más accesible.
Llamada telefónica. Al otro extremo del alambre, la voz de un niño suena: “Todavía no hemos aprendido fracciones”. ¡Pero enseñamos la mitad! Aquí está la respuesta a todas las preguntas. Zemskov vuelve a resolver el problema de la tercera clase y piensa como un estudiante debe pensar.
El maestro aborda el problema a través del juego: “Si las escalas están en equilibrio, entonces las escalas pueden ser agregadas.” Es lo mismo con la igualdad. Podemos doblarlos juntos a la izquierda y a la derecha”. Peter sugiere añadir un ejemplo con respuesta 13 y un ejemplo con respuesta 6. Recuerde que 2 de estos ejemplos son los mismos.

Como vemos la adición en el primer ejemplo (con la respuesta 13) y la resta en el segundo ejemplo, los mismos números simplemente desaparecen cuando se añade. El único número desconocido se añade dos veces. "Dos cubos como este son trece más seis", explica el maestro, señalando a la plaza en la esquina inferior izquierda. 13 + 6 = 19, y 19 ÷ 2 = 9,5.

Y entonces todo se resuelve muy simplemente. Sustituir 9.5 en el lugar correcto y calcular cuánto necesita para restar de este número para obtener 6. La acción es simple, así que ni siquiera necesitamos grabarla.
El resultado es: 9.5 - 3.5 = 6. Recuerde que los números en el cuadrado inferior derecho y superior izquierdo son los mismos. Queda por descubrir lo que hay en la última plaza. Aquí vamos. 3.5 + 4.5 = 8.
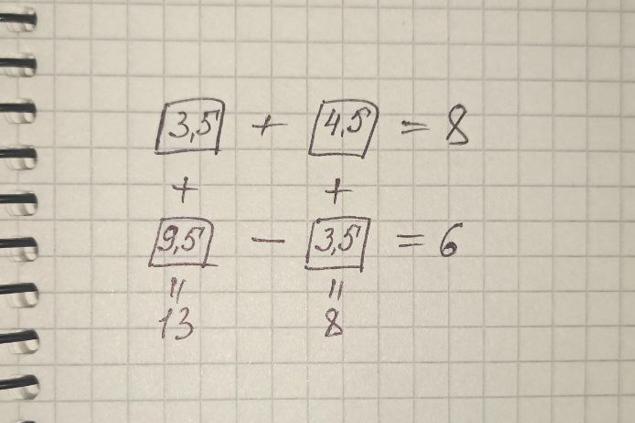
Dime, ¿te las arreglaste para resolver este problema? Por cierto, sería genial si pusieras un ejemplo para tus hijos. Comparte en los comentarios si lograron hacer frente a ella. ¡Espérate abajo!
Alexandra imperdonable de “Moscow no cree en las lágrimas” cumplió 63 años, cómo vive la actriz
Me encantan los coches alemanes, pero cuando me mudé a Alemania, me decepcionó.