153
A third-grader's mental torture from Kazakhstan, can you decide?
My favorite math teacher, Peter Zemskov, keeps throwing food for our minds. Recently, on his YouTube channel, he offered subscribers. solve the problem of the third class. It would seem that it can be difficult? That's the beauty!

Schoolchildren click these problems like nuts. Adults, on the other hand, have to work hard to find the right answer. I wonder if you can do it.
First of all, I suggest you look at the problem that we have to solve today. Think about where to start and how best to approach an example in a way that makes it the fastest. And then I'll tell you how the math teacher decided it.

Peter Zemskov is an experienced mathematics teacher. So when his nephew from Kazakhstan called him and offered to solve the problem of the third class, the man immediately responded. The only problem is that he started to decide as an adult.
Zemskov determined that there are three variables in the example. We pause right now. Why three instead of four? It's simple! Two of the four examples result in 8. To the number that is in the upper right square, you need to add the same number to get 8.

This knowledge helped Peter to compose the system and present the unknown variables as follows: + y = 8, + z = 13, z - = 6. And at this stage, the mathematician realized that third-graders do not yet know how to solve such equations. There must be a simpler and more accessible way.
Phone call. At the other end of the wire, a child’s voice rings out: “We haven’t learned fractions yet.” But we taught half! Here's the answer to all the questions. Zemskov returns to solving the problem of the third class and thinks as a student should think.
The teacher approaches the problem through the game: “If the scales are in equilibrium, then the scales can be added.” It's the same with equality. We can fold them together on the left and right.” Peter suggests adding an example with answer 13 and an example with answer 6. Remember that 2 of these examples are the same.

Since we see addition in the first example (with answer 13) and subtraction in the second example, the same numbers simply disappear when added. The only unknown number is added twice. "Two cubes like this are thirteen plus six," the teacher explains, pointing to the square in the lower left corner. 13 + 6 = 19, and 19 ÷ 2 = 9.5.

And then everything is solved very simply. Substitute 9.5 in the right place and calculate how much you need to subtract from this number to get 6. The action is simple, so we don’t even need to record it.
The result is: 9.5 - 3.5 = 6. Remember that the numbers in the lower right and upper left square are the same. It remains for us to find out what is in the last square. Here we go. 3.5 + 4.5 = 8.
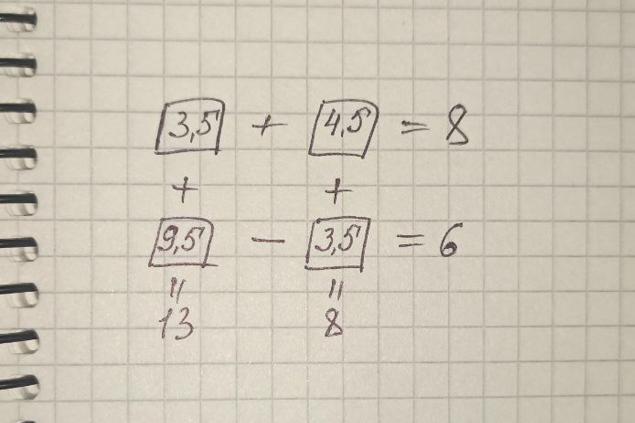
Tell me, did you manage to solve this problem? By the way, it would be great if you set an example for your children. Share in the comments whether they managed to cope with it. Wait for you downstairs!

Schoolchildren click these problems like nuts. Adults, on the other hand, have to work hard to find the right answer. I wonder if you can do it.
First of all, I suggest you look at the problem that we have to solve today. Think about where to start and how best to approach an example in a way that makes it the fastest. And then I'll tell you how the math teacher decided it.

Peter Zemskov is an experienced mathematics teacher. So when his nephew from Kazakhstan called him and offered to solve the problem of the third class, the man immediately responded. The only problem is that he started to decide as an adult.
Zemskov determined that there are three variables in the example. We pause right now. Why three instead of four? It's simple! Two of the four examples result in 8. To the number that is in the upper right square, you need to add the same number to get 8.

This knowledge helped Peter to compose the system and present the unknown variables as follows: + y = 8, + z = 13, z - = 6. And at this stage, the mathematician realized that third-graders do not yet know how to solve such equations. There must be a simpler and more accessible way.
Phone call. At the other end of the wire, a child’s voice rings out: “We haven’t learned fractions yet.” But we taught half! Here's the answer to all the questions. Zemskov returns to solving the problem of the third class and thinks as a student should think.
The teacher approaches the problem through the game: “If the scales are in equilibrium, then the scales can be added.” It's the same with equality. We can fold them together on the left and right.” Peter suggests adding an example with answer 13 and an example with answer 6. Remember that 2 of these examples are the same.

Since we see addition in the first example (with answer 13) and subtraction in the second example, the same numbers simply disappear when added. The only unknown number is added twice. "Two cubes like this are thirteen plus six," the teacher explains, pointing to the square in the lower left corner. 13 + 6 = 19, and 19 ÷ 2 = 9.5.

And then everything is solved very simply. Substitute 9.5 in the right place and calculate how much you need to subtract from this number to get 6. The action is simple, so we don’t even need to record it.
The result is: 9.5 - 3.5 = 6. Remember that the numbers in the lower right and upper left square are the same. It remains for us to find out what is in the last square. Here we go. 3.5 + 4.5 = 8.
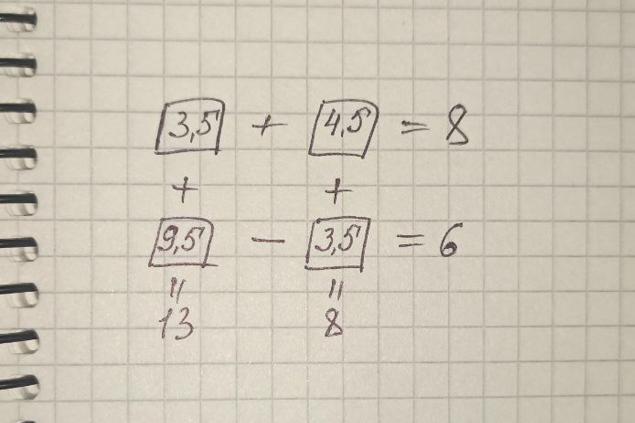
Tell me, did you manage to solve this problem? By the way, it would be great if you set an example for your children. Share in the comments whether they managed to cope with it. Wait for you downstairs!
Unforgettable Alexandra from “Moscow does not believe in tears” turned 63, how the actress lives
I love German cars, but when I moved to Germany, I was disappointed.