Программный баг

Так получилось, что я лежу в больнице. В чужом городе. Скукотиииища! Связи – нет, так что если этот опус опубликован – значит, я уже вернулся домой. Хочется что-то написать для души. Но что? Вертолётные темы не пошли – второй пост не вышел из инкубатора, так что с ними завязываем. Другие подобные темы – у меня фоток разобранных не было заготовлено, да и уже сомневаюсь, пойдут ли. Добыть фотик и поиграть в блоггера, фоткая больницу? А смысл? О чём же порассуждать? Так получилось, что я не так давно разъяснял устно сыну школьнику про системы счисления. Самое удивительное – у меня получилось, он понял. Давайте попробую изложить то же самое, но письменно. Да, мне нечего делать, я же в больнице. Ожидается 17 весьма условных картинок. Не ломайте! О конце сообщу. А начнём мы с анекдота:





Счёт по нарастающей
Чему нас учат в первом классе? Что есть единицы, десятки, сотни. Досчитали до конца единиц – переходим к десяткам. Перебрали десятки – переходим к сотням. Дальше – уже тема второго класса, так что остановимся пока на этом. Откуда взялись вообще десятки? Есть мнение, что всё связано с тем, что у нас на руках 10 пальцев. Ну, а дальше – по нарастающей. И почему-то учителя забывают сказать, что вся эта неоднородность – выдумана. Вроде, она помогает освоить счёт в целом, но в нашем случае – только путает. Давайте перейдём от неоднородных понятий к однородным. Сначала напишем с детства нам знакомую таблицу

0 1 2 3 4 5 6 7 8 9

И договоримся, что мы перебираем числа в том порядке, в каком они в таблице идут. Сначала 0, потом 1, потом 2… Ну и так до 9. А что дальше? А введём-ка мы понятие разряда. Эти разряды будут идти справа налево (так повелось, ничего не попишешь).

Число 5 – одноразрядное. Его описывать не интересно. То же скажем и о двухразрядном числе 83.

Число 987 – трёхразрядное, вот о нём уже поговорим. Младший разряд равен 7, следующий равен 8, следующий – 9. В чём-то немцы правы, когда читают числа справа налево. Может, их язык древние программисты создавали?



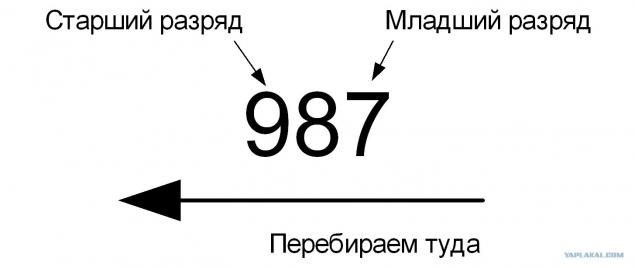
И тогда мы просто введём правило увеличения для разряда



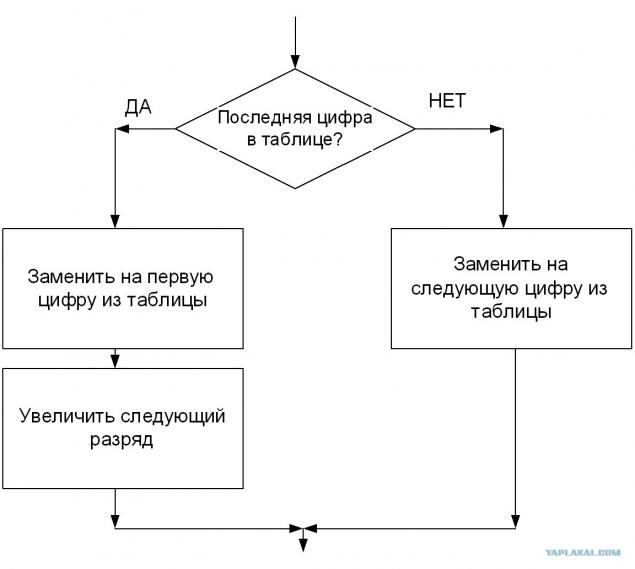
Всегда начинаем с младшего (правого) разряда.

Вот у нас число 987. Мы запустили процесс его увеличения. В младшем разряде у нас цифра 7. Следующая в таблице – 8. Получаем 988.

Ещё разок. Младший разряд равен 8. Следующая в таблице – 9. Получаем 989.

И ещё разок. Младший разряд равен 9. Хм. Конец таблицы. Хорошо, меняем на 0 и переходим к следующему разряду. Он равен 8. Следующая цифра в таблице – 9. Получаем 990.

Работает! Мы больше не привязаны к разнородным понятиям «единицы», «десятки», «сотни», «тысячи» и тому подобное. У нас есть текущий разряд и следующий разряд. Мы всегда начинаем работу с крайне правого, а дальше – как повезёт. Для числа 19999999 фраза «меняем на первый элемент таблицы, то есть, на 0 и увеличиваем следующий разряд» будет повторяться многократно. Но рано или поздно мы упрёмся в: «Текущий разряд равен 1, берём следующее число из таблицы – 2, получаем 20000000».

Согласитесь, что при устном увеличении мы примерно так же делаем, просто не проговариваем эти операции, так как довели их до автоматизма в младших классах. Но округляя цену 4999,99, видя её на рекламе, мы невольно бежим глазами справа налево, чтобы понять, где остановиться, особенно если цена, скажем, 24999,99.

А, чуть не забыл. Если в разряде ничего нет, то считаем, что там 0, то есть, 99, 099, 000099 – одно и то же, ведь так?

Переместимся теперь с планеты Земля на мультяшную планету Плюк. Мультяшные пацаки и чатлане – четырёхпалые, это бросается в глаза, когда они из-за спичек в пепелаце торгуются (говорят «Шесть» и выбрасывают одну полную ладонь и два пальца на другой руке). Видео того эпизода вставлять не буду, я не хочу сразу после больницы в тюрьму попасть. Но найду что-нибудь в Гугле из уже валяющихся в сети картинок.