740
10目瞪口呆的事实有关数学的,将请即使是人文学科
即使你不明白的数学一无所知,即使学校讨厌的主题,即使认为自己是纯粹的以人为本......在一般情况下,在任何情况下 - !你喜欢的事实,网站保证
1 STRONG>英国数学家亚伯拉罕·棣莫弗老年一旦发现睡眠增加了持续时间为每天15分钟。在作出一个等差数列,他把它何时会达到24小时日期 - 1754年11月27日。 在这一天,他死了。 STRONG>
2 STRONG>宗教的犹太人正试图避免所有的基督教的象征和标志,类似于交叉。例如,学生一些以色列的学校,而不是一个“+”号书面重复倒“T»。
3 STRONG>欧元纸币的真伪可以通过它的序列号,信和十位进行检查。您需要替换其序号字母英文字母,数字加起来与它的其余部分,然后把结果数,直到你得到一个数字。如果这个数字 - 8,说明是真实的
。

另一种方法是检查折叠这样的数字,而不是字母。一个字母和数字的结果,必须一个特定的国家相匹配,因为欧元被印刷在不同的国家。例如,在德国是X2。
4 STRONG>据认为,阿尔弗雷德·诺贝尔没有包括在数学保费学科名单由于这样的事实,他的妻子欺骗了他一个数学家。 事实上,诺贝尔从未结婚。 STRONG>
真正的原因是忽视了数学的诺贝尔奖是未知的,但也有一些假设。例如,在那个时候已经存在数学奖由瑞典国王。其他的 - 数学不要让人类的重要发明,因为这门科学是纯粹的理论
。
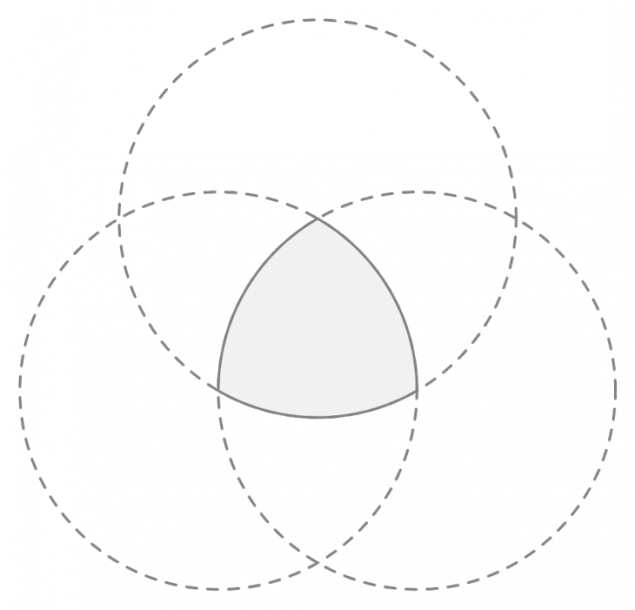
的 5. 强>鲁洛三角形 - 由半径相等的三个圆一个中心在等边三角形具有一个侧的顶点相交形成的几何图形。钻头是由三角形的基础上鲁洛允许钻方孔(不准确2%)。
6 STRONG>俄罗斯数学文献不为零的自然数,而在西方,相反,属于自然数集。
7 STRONG>美国数学家乔治·丹,作为一个研究生的大学,一次迟到的教训并接受写在黑板上方程的功课。在他看来,比平时更难,但过了几天,他能够实现它。原来,他决定在这打过许多科学家统计两个“无法解决的问题”。
8。所有的数字在轮盘赌平等“的号码兽”的总和 - 666 STRONG>
9 STRONG>柯瓦列夫斯卡娅会见了数学在幼年时期,当它没有足够的空间壁纸,而不是它被粘贴片上微积分Ostrogradskii讲座。
10 STRONG>在印第安纳州于1897年发布了该法案,建立圆周率到3的值,2。此法案没有通过大学教授的及时干预成为法律的立法。
通过 factroom.ru
1 STRONG>英国数学家亚伯拉罕·棣莫弗老年一旦发现睡眠增加了持续时间为每天15分钟。在作出一个等差数列,他把它何时会达到24小时日期 - 1754年11月27日。 在这一天,他死了。 STRONG>
2 STRONG>宗教的犹太人正试图避免所有的基督教的象征和标志,类似于交叉。例如,学生一些以色列的学校,而不是一个“+”号书面重复倒“T»。
3 STRONG>欧元纸币的真伪可以通过它的序列号,信和十位进行检查。您需要替换其序号字母英文字母,数字加起来与它的其余部分,然后把结果数,直到你得到一个数字。如果这个数字 - 8,说明是真实的
。

另一种方法是检查折叠这样的数字,而不是字母。一个字母和数字的结果,必须一个特定的国家相匹配,因为欧元被印刷在不同的国家。例如,在德国是X2。
4 STRONG>据认为,阿尔弗雷德·诺贝尔没有包括在数学保费学科名单由于这样的事实,他的妻子欺骗了他一个数学家。 事实上,诺贝尔从未结婚。 STRONG>
真正的原因是忽视了数学的诺贝尔奖是未知的,但也有一些假设。例如,在那个时候已经存在数学奖由瑞典国王。其他的 - 数学不要让人类的重要发明,因为这门科学是纯粹的理论
。
的 5. 强>鲁洛三角形 - 由半径相等的三个圆一个中心在等边三角形具有一个侧的顶点相交形成的几何图形。钻头是由三角形的基础上鲁洛允许钻方孔(不准确2%)。

6 STRONG>俄罗斯数学文献不为零的自然数,而在西方,相反,属于自然数集。
7 STRONG>美国数学家乔治·丹,作为一个研究生的大学,一次迟到的教训并接受写在黑板上方程的功课。在他看来,比平时更难,但过了几天,他能够实现它。原来,他决定在这打过许多科学家统计两个“无法解决的问题”。
8。所有的数字在轮盘赌平等“的号码兽”的总和 - 666 STRONG>
9 STRONG>柯瓦列夫斯卡娅会见了数学在幼年时期,当它没有足够的空间壁纸,而不是它被粘贴片上微积分Ostrogradskii讲座。
10 STRONG>在印第安纳州于1897年发布了该法案,建立圆周率到3的值,2。此法案没有通过大学教授的及时干预成为法律的立法。
通过 factroom.ru























