15 оптических иллюзий для настоящих ценителей

Люди относятся к оптическим иллюзиям по-разному, но большинству приносит истинное удовольствие ломать голову над той или иной загадкой.

Сайт предлагает вашему вниманию любопытную подборку из 15 оптических иллюзий для настоящих ценителей.

Спираль Фрейзера

Эта так называемая ложная иллюзия образуется с помощью наложенных друг на друга сегментов, как будто формирующих спираль, однако на самом деле это обычные круги.





Иллюзия Эббингауза







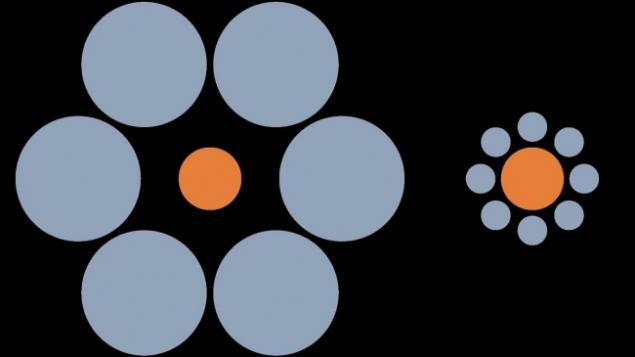
Оптическая иллюзия восприятия относительных размеров, носящая имя немецкого психолога Германа Эббингауза. Версия этой иллюзии заключается в том, что два одинаковых по своим размерам круга помещаются рядом, причем вокруг одного из них находятся круги большого размера, тогда как другой окружен мелкими кружками; при этом первый круг кажется меньше второго.





Иллюзия невозможного куба







Этот невозможный куб был создан Чарльзом Кокраном в 1966 году. Ощущение глубины в этом кубе создается с помощью неправильных соединений. Даже не пытайтесь разгадать секрет этой нереальной фигуры.

Иллюзия Цёлльнера

Оптическая иллюзия Цёлльнера заключается в том, что параллельные линии, пересеченные множеством коротких диагональных отрезков, кажутся расходящимися. Немецкий астрофизик Иоганн Цёлльнер заметил этот эффект случайно в 1860 году, когда разглядывал ткань.





Иллюзия Джастроу







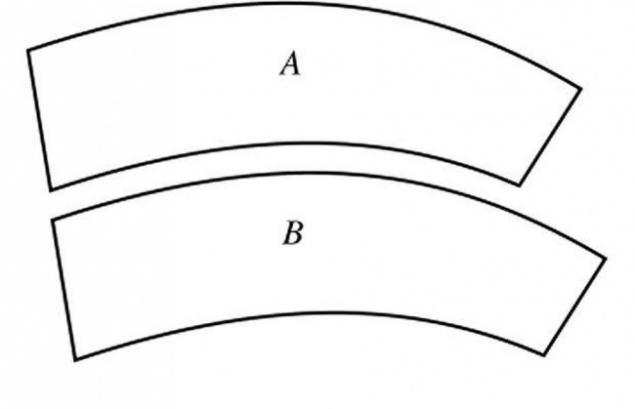
Иллюзия, «открытая» американским психологом Джозефом Джастроу, заключается в том, что две абсолютно идентичные по размеру и форме фигуры, расположенные определенным способом, кажутся нам несоразмерными.

Треугольник Канижа

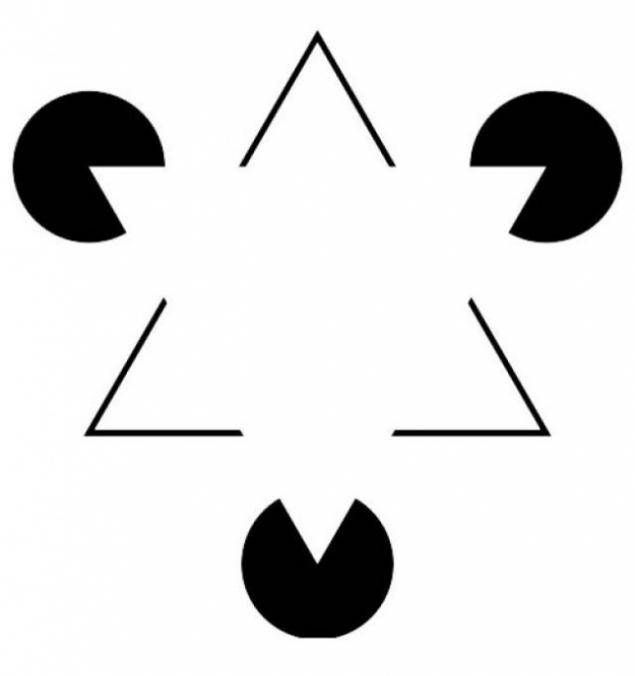
Эта иллюзия была названа в честь итальянского физиолога Гаэтано Канижа. Чтобы доказать, что люди видят окружающую действительность не «как есть», а через особые фильтры — ментальные модели, он нарисовал комбинацию из различных геометрических фигур, среди которых нет белого треугольника, однако наши глаза не соглашаются с этим.

Иллюзия Поггендорфа

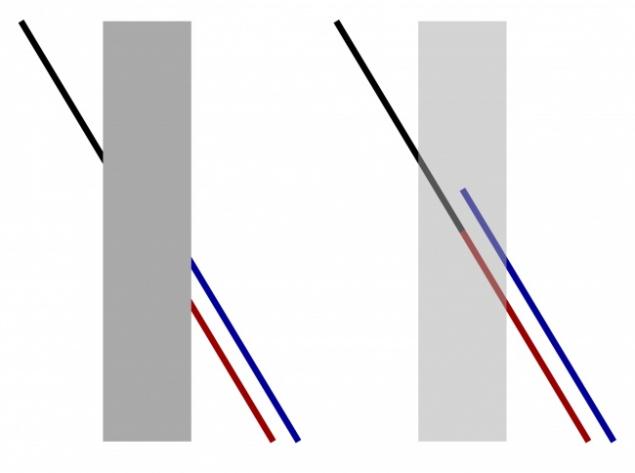
Классическая оптическая иллюзия, названная в честь немецкого физика Иоганна Поггендорфа. Ученый обнаружил ее в рисунке, который ему прислал известный астрофизик И. Цёлльнер. Суть данной иллюзии заключается в том, что на рисунке справа продолжением черной линии является красная линия, а не синяя, как представляется на первый взгляд. Любопытно, что до настоящего времени нет ни одного объяснения этого оптического эффекта.

Бливет

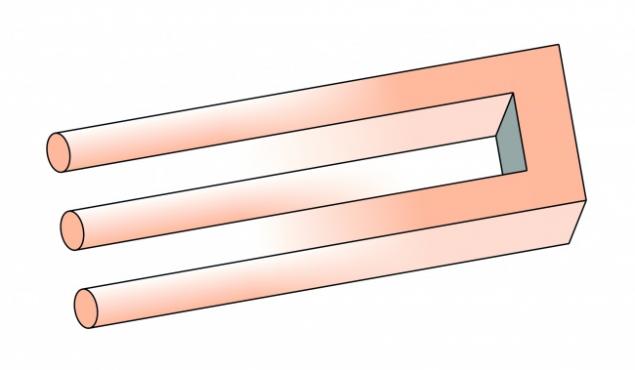
Бливет, он же «невозможный трезубец», являет собой яркий пример геометрической иллюзии. Как бы вы ни старались, у вас не получится понять эту фигуру, так как ее попросту не существует.

Иллюзия Уайта

На первый взгляд данная иллюзия противоречит здравому смыслу — абсолютно одинаковые оттенки серого цвета кажутся разными из-за своего соседства с противоположными цветами — черным и белым.

Иллюзия движения

При наличии определенных цветовых контрастов и формы изображенных предметов нашим глазам начинает казаться, будто совершенно статичное изображение начинает двигаться.

Иллюзия Лудимара Германна

Это оптическая иллюзия открыта Лудимаром Германном в 1870 году, во время чтения трудов Джона Тиндаля о звуке. На изображении появляются «призрачные» серые пятна на пересечении белых (или светлых) линий, расположенных на черном фоне. Эти пятна исчезают, если смотреть непосредственно на место пересечения.

Пожилая пара, или песни под гитару

Взгляните на эти нежные отношения пожилой пары. А теперь взгляните повнимательнее, быть может, вы увидите другую картину?

Иллюзия вращающегося вокруг точки круга

Сфокусируйте свой взгляд на черной точке в центре круга, затем немного покачайте головой. Если вы посмотрите на картинку снова, то внешние круги начнут вращаться в противоположных направлениях.

Иллюзия «Стена кафе»

При первом знакомстве с картинкой вам наверняка покажется, что на ней изображены изогнутые линии, однако на самом деле они параллельны друг другу. Этот эффект был обнаружен Ричардом Грегори в кафе Wall в Бристоле. Отсюда и пошло ее название.

Иллюзия крутящихся колес

Во время знакомства с этой картинкой к вам непременно придет ощущение, что колеса на ней начинают крутиться, причем в разные стороны. Если же обратить пристальный взгляд на какое-то одно колесо, то оно перестанет крутиться, в отличие от всех остальных.



По материалам: The Telegraph



13 оптических иллюзий, сбивающих с толку
15 иллюзий, которые взорвут ваш мозг

via adme.ru/tvorchestvo-hudozhniki/15-illyuzij-kotorye-vzorvut-vash-mozg-465405/