2408
Лікбезь на картографічних проекціях з фотографіями
Візуалізація даних різних видів, що мають певний географічний розподіл, останнім часом стала більш поширеною. Тут, на Хабра, статті з картами виявляються майже на тиждень. Карти в статтях дуже різні, але вони мають одну річ в загальній: як правило, вони використовують тільки два карткові проекції, а не найуспішніші з існуючих. Я хотів би дати вам деякі приклади проекцій, які виглядають більш естетично і краще підходять для різних видів візуалізації. Ця стаття буде виглядати на глобальних проекціях і проекціях більшості Землі, як візуалізація чогось на карті світу, можливо, найбільш поширена з цих завдань.
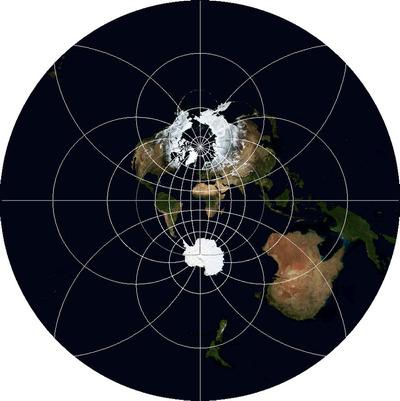
Оскільки стаття орієнтована на візуалізацію даних, я не поглиблюся в теорію проекцій (сумки, відповідність, рівновага і т.д.), крім загальних принципів їх будівництва. Я також поговорю тут проекцій, формально звертаючись до координаційної довідкової системи, оскільки вона не має сенсу для карт цього масштабу до окремої проекції та дати. Тут немає математики, крім простої геометрії. Ті, хто бажає дізнатися про математичні принципи, можуть зробити це через статті на Wolfram MathWorld. Для студентів програмування в галузі геоінформаційних систем або їх досвідчених користувачів ця стаття не може бути дуже корисною.
Перед тим як почати, я поясню кілька речей. Всі приклади будуть надані за допомогою національних даних, що містяться в цьому сайті, і наведено на основі даних променевого покоління НАСА. Останні додані синтехічні зображення поверхні Землі для кожного з дванадцять місяців 2004 року, що дозволить отримати деякі різноманітні ілюстрації.
Я хотів відкрити програмне забезпечення дуже багато, але використовуючи GDAL в цьому випадку, здається неефективним для мене - деякі не дуже запущені, але корисні проекції в його реалізації в даний момент або не існує, або я не виглядав на вихідний код, і тому я підготували ілюстрації в комерційній програмі GlobalMapper, які я використовую протягом багатьох років, і які відомі для підтримки вражаючого списку координатних систем.
Я даю імена проекцій і деякі умови англійською мовою, тому що якщо хтось хоче шукати матеріали на цій темі, є кілька менш російськомовних джерел в мережі (кількість статей у Вікіпедії в Росії кілька разів менше). Для більшості проекцій я спробую дати не тільки імена, але й коди EPSG та/або WKID, а також назву проекції в бібліотеці PROJ.4, широко використовується в програмному забезпеченні відкритого джерела (наприклад, пакет R) для підтримки координатних систем.
Деякі проекції можуть бути знайомі з кимось з картинки xkcd, але всі вони не будуть розглянуті тут.
Почнемо з тим, що найбільш поширені проекції, і що їх неправильно.
Географія проекції, Latitude/Longitude, Plate carrée EPSG:4326 WKID:54001 PROJ.4:longlat. Строго кажучи, це не зовсім проекція, оскільки вона виходить шляхом інтерпретації полярних кутових координат як лінійних прямокутних координат, без будь-яких обчислень. Ця проекція використовується тому, що вона здатна відображати всю поверхню Землі і тому, що це найпростіше математично, і дані дуже часто пропаговані непроектовані, тобто в географічних координатих (відчуття широтності і довготи).
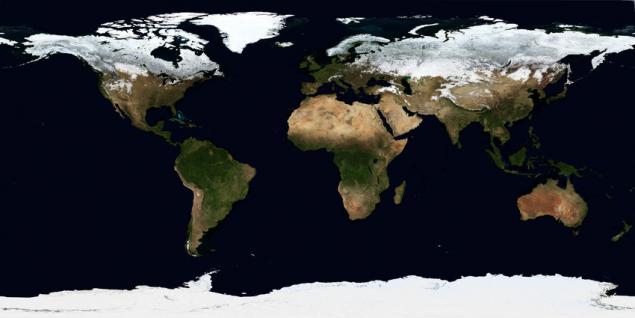
Що відбувається? Виявляється прямокутник, де фіксуються стовпні точки в лініях (верхова та нижча гра). Далі від еквалайзера, більш міцний будь-який об'єкт на карті, вирівнюється вертикально і простягається горизонтально. Як я сказав, що це досить добре для відображення глобальних даних, але полярні території (Канада, Норвегія, Швеція, північна Росія, Фінляндія, Грінланд, Антарктика, Ісландія) спотворюються. Проекції, які не можуть бути обговорені пізніше. Єдина причина використання цієї проекції є її екстремальною простотою впровадження програмного забезпечення - вам просто потрібно на карті координатної системи від -180o до 180o до X і від -90o до 90o до Y до площини, враховуючи лінійні кутові одиниці.
Ще один популярний проекція мерця PROJ.4:merc. Він також використовується для візуалізації даних, що охоплюють весь світ, але його популярність диктується не тільки простотою - його варіанти є дефакто стандартом для глобальних картографічних послуг, таких як Google Maps, Bing Maps, тут. Він глибоко пов'язаний з бібліотекою OpenLayers, Leaflet, API вищевказаних сервісів. У варіанті Google і OpenStreetMap він називається Web Mercator і має код EPSG / WKID:3857, іноді також називають EPSG:900913. Принцип його побудови не набагато складніший, ніж географічний - це проекція на циліндрі, вісь якого збігається з географічною віссю Землі, проекція виникає по лініях, що залишають центр планети, з яких похибка розтягування окружних регіонів горизонтально компенсується пропорційним розтягуванням по вертикалі. Єдина проблема з цим є те, що карта занадто велика вертикально, якщо ви намагаєтеся на карті на північ від Greenland. Таким чином, 16° полярних регіонів зазвичай викидаються (в рівній пропорції або більше з півдня).

У деяких очах людей виглядає трохи краще, ніж Географічна, але одна проблема вже згадувала, а другий - тим, що чим ближче об'єкт до стовпів, тим більше він з'являється, хоча його форма не так спотворюється. Таким чином, якщо об'єкт візуалізації є щільність маркерів на одиницю території або відстані, цей метод відображення буде вводитися в оману. З грамотним вибором способу візуалізації, звичайно, це можна компенсувати, і для деяких випадків це не проблема на всіх: наприклад, якщо значення деякого показника в всій країні корелюється з кольором цієї країни на карті, ефект розтягування ділянки не впливає. Ця проекція зберігає лише форму об'єктів, тому намітки материків і країн досить визнаються. І як я сказав, що це ваш перший і простий варіант при створенні інтерактивних веб-карт.
Що робити з глобальними даними, якщо з якихось причин нам необхідно проекція, яка краще зберігає властивості об'єктів, таких як форма, площа, відстані та кути? Закони геометрії не дозволяють зберегти всі ці властивості одночасно, розгортаючи круглу поверхню Землі на площині. Однак для візуалізації даних, естетики та сприйняття є найважливішими, а не збереження властивостей, як для навігації або виконання завдань. Тому можна вибрати проекцію, в якій спотворення будуть рівномірно розподілені за властивостями. І є досить багато таких проекцій. Є три найвідоміших, з схожими властивостями: Winkel Tripel WKID: 54042 PROJ.4:винтри, Проекція Робінсона WKID: 54030 PROJ.4:робін, Каврський проекція. Першими і останніми мають мінімальні візуальні спотвори, і дуже важко відрізняти їх без перегляду сітки, тому я даю ілюстрацію для Winkel Tripel, оскільки один я особисто схожий на найбільш.
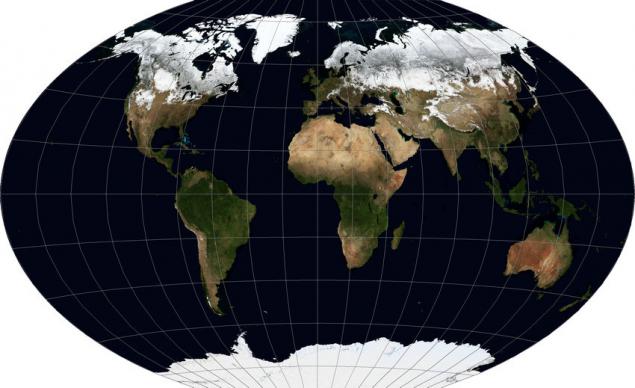
Як виглядає опис цієї проекції в форматі ESRI WKT:
PROJCS["Robinson", GEOGCS["GCS_WGS_1984", DATUM["D_WGS84", SPHEROID["WGS84", 6378137,298.257223563], PRIMEM["Greenwich",0], UNIT["Degree", 0.017453292519943295] ], ПРОЕКТІЯ["Roson", PARAMETER["central_meridian",0], PARAMETER[false][false][false][false], UNIT[0]
Як легко побачити, хоча спотворення контурів і невелике збільшення площі країн до стовпів також спостерігаються, але це навіть не може бути порівняно з розтягуванням географічного проекції і пропорційним збільшенням проекції мерця.
Тут ви повинні зробити невеликий з'їзд і звернути увагу на те, що перегляд за замовчуванням цього проекції страждає від одного недоліку, що стосується інших глобальних проекцій. Справа в тому, що якщо центральний меридіан – лінія підключення північних і південних полюсів через центр карти (довга походження) – береться як нуль меридіан, то карта буде нарізана на 180-му. Але третина Чукотки буде на лівому краю карти, а дві третини праворуч. Щоб зробити карту більш красивою, ріжуча повинна бути десь навколо 169-го західного меридіанського східного острова Ратманова, для якого 11-й слід приймати як центральний. Ось ілюстрація того, що відбувається:
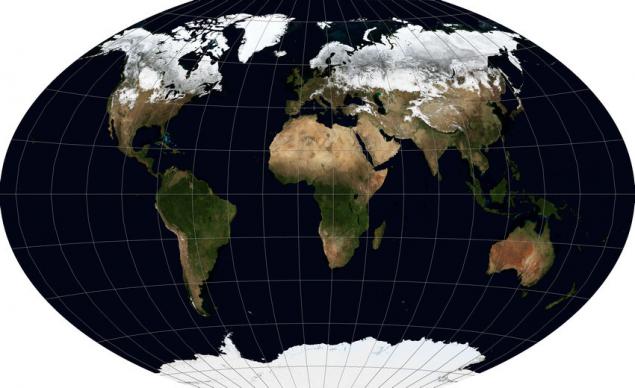
Ось модифікований опис в ESRI WKT:
PROJCS["Robinson", GEOGCS["GCS_WGS_1984", DATUM["D_WGS84", SPHEROID["WGS84", 6378137,298.257223563], PRIMEM["Greenwich",0], UNIT["Degree", 0.017453292519943295], ПРОЕКТІЯ["Roson"], PARAMETER["central_meridian",11], PARAMETER[false][feasting"false], PAth[0]
У форматі координатної системи для PROJ.4 довгота проекційного центру надається +лон_0=.
11-й меридіан – це «магічний» номер: майже всі світові проекції, які мають рівномірну вагу вздовж еквалатора, можна розрізати вздовж Берінгової протоки, якщо вона береться як центральний, так і не нульовий.
Зауважте, що придумці про вибір проекції варто враховувати всі існуючі реальні вимоги до візуалізації. Наприклад, якщо дані відносяться до клімату, це може бути сенсом або картою широтних ліній або використовувати проекцію, де вони горизонтальні, а не згинаються до країв карти (тобто відмовитися від Трійки Winkel на користь, наприклад, Робінсон). У цьому випадку це полегшить і більш точну оцінку відносної близькості від різних місць до стовпів і еквалатора. Ще одним значним плюсом проекції Робінсона є те, що він підтримує багато програмного забезпечення, в тому числі відкриті джерела, а деякі інші не можна сказати.
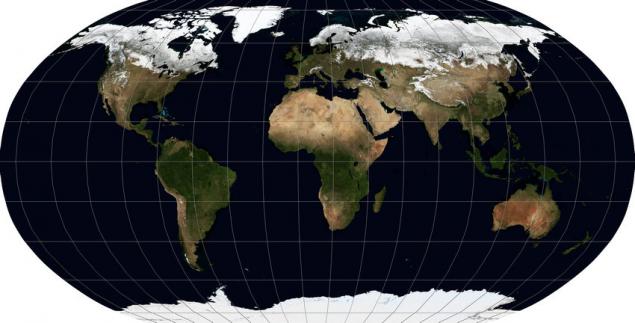
Іноді, коли необхідно зберегти деякі властивості якомога простіше, наприклад, співвідношення площі об'єктів (знижок) - естетична сторона страждає. Але оскільки це ще може знадобитися для чогось, я даю один приклад такої проекції – проекція Моллвейда WKID: 54009 PROJ.4:молл.
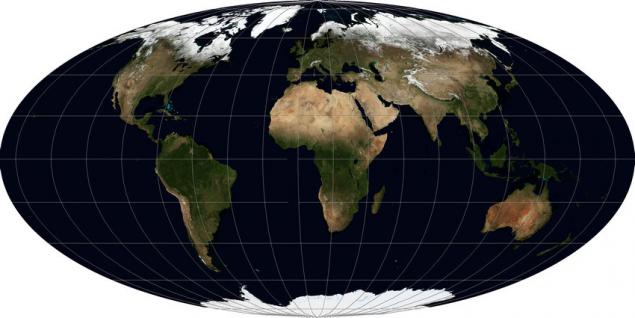
Як ви можете побачити, це досить схоже на проекцію Робінсона, але з різницею, що стовпи ще затягуються в точки, що робить форму окружних регіонів дуже спотворена. Але пропорції області країн, що вимагаються, значно краще зберігаються.
Наймолодший конкурент цих проекцій – природна ЗемляПРОЙ.4: проекція натур – це гібрид проекцій Кавражського та Робінсона, а його параметри були обрані групою американських, швейцарських та словенських фахівців у 2007 році, тоді як вік більшості картографічних проекцій не менше половини століття.
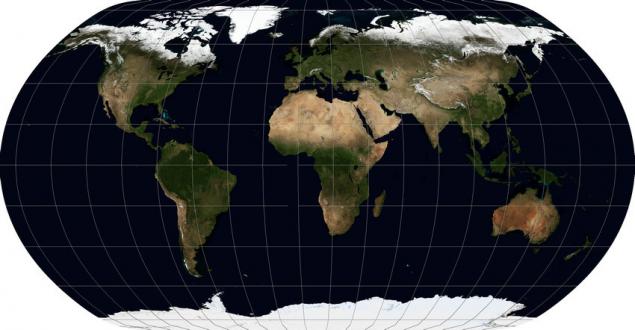
Є ряд інструментів, які були написані спеціально для цієї мети, але його підтримка далеко від ubiquitous.
Звичайно, всі проекції не закінчуються. Винайдено багато з них. Деякі просто дивляться дивні (са, проекція Bonnet зображує Землю як фігуру, що нагадує ріжучий яблуко або стилізоване серце), деякі призначені для спеціальних ситуацій. Наприклад, я б хотів би, що багато людей побачили карту світу в картинках, які виглядають як індинська скоринка, яка була видалена і плащена. Це, ймовірно, Goode's Interrupted Goode Homolosine projection WKID:54052.
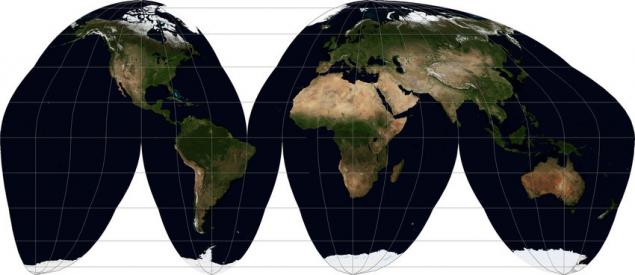
Її зовнішній вигляд досить гідний назви. Його мета полягає в тому, щоб відображати розмір об'єктів (і в певній мірі форма) близько до природних пропорцій. Його головна проблема, крім свого імені і дивного зовнішнього вигляду, полягає в тому, що вибравши центральний меридіан, неможливо переконатися, що не великий шматок землі вирізається. Щось з переліку обов’язково постраждає: Грінланд, Ісландія, Чукотка, Аляска. Особисто, на мій погляд, легше надати окремі зображення країн, ніж використовувати таку карту, якщо ви не хочете стилізувати вашу роботу на середину XX століття.
Є проекції, які не є універсальними в природі, але я хотів би подивитися на них тут, тому що вони здатні показати світ, який є своєрідним виглядом планети з космосу. Вертикальний проекційний проекційний проекційний проект (WKID: 54049) Особливою властивістю є показати поверхню землі в такій перспективі, як вона виглядає з певної висоти. Висота над еліпсоїдом (ідеалізовані моделі фігури Землі) дається для цього проекції в явному вигляді.
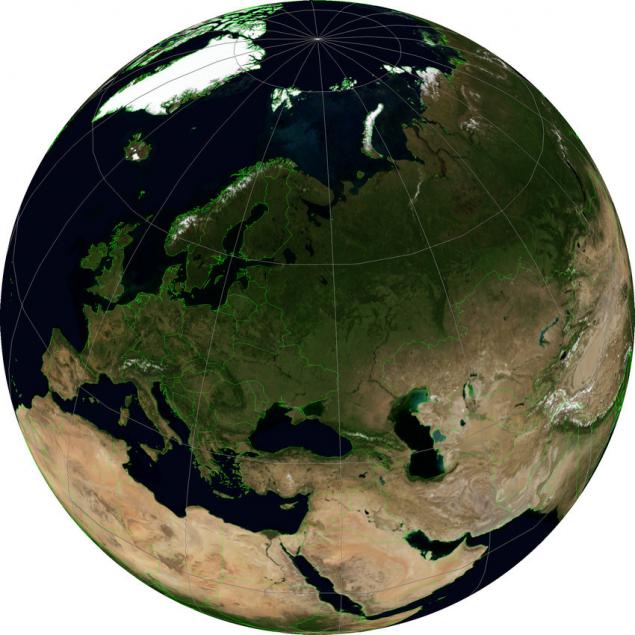
У ілюстрації цей проекція має широту і довготу центру, що дорівнює широтості і довготи Москви, а висота 5000000 метрів. Чим більша ця відстань, тим сильніше зображення Землі стає схожим на його зображення в проекції ми розглянемо останнє.
Проекція, яка показує паралельний вигляд Землі з нескінченної відстані називається Ортографічним виступом WKID:43041 PROJ.4:ortho. Якщо ви не використовували Google Earth. Я кажу, що в сенсі, тому що "режим альтанки" в цьому проекції завжди перпендикулярно поверхні Землі, тоді як в Google Earth можна нахилити як вам подобається.
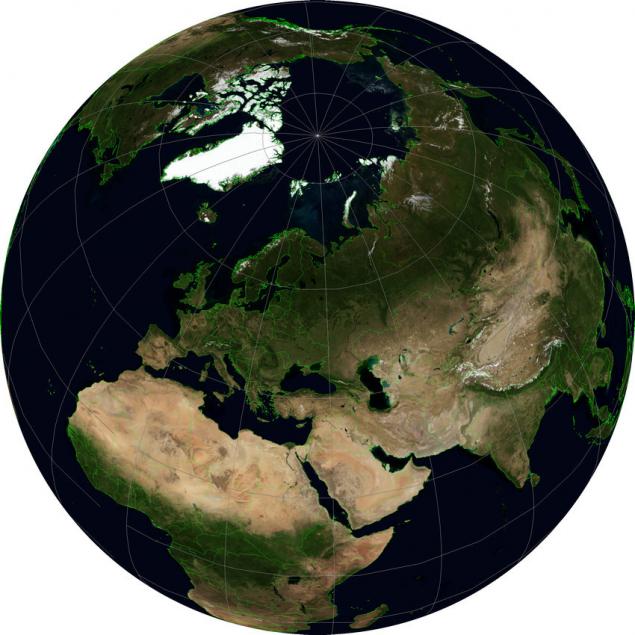
Для цього, як для попередньої проекції, можна вказати центральну широту і довготу, щоб орієнтуватися на Землю за бажаним способом. Наприклад, ви можете показати півсферу з центром в певній точці питання – наприклад, ілюструвати континентальні витрати трафіку, що генеруються з одного підприємства. Створення двох карт з протилежними координуючими значеннями, ви можете отримати карту усього світу (хоча по краях спотворення буде дуже великим). Створення послідовності карт з гладкою зміною в центральній точці дасть кадри для анімації обертальної планети без тривимірної графіки.
Якщо стаття доведе цікаве, я намагаюся писати про проекції, які використовуються для відображення окремих країн або регіонів, спрямованих на те, що ця стаття, на базових властивостях цих проекцій для задачі візуалізації даних, інфографіка та вподобання.
Джерело: habrahabr.ru/post/235283/

Оскільки стаття орієнтована на візуалізацію даних, я не поглиблюся в теорію проекцій (сумки, відповідність, рівновага і т.д.), крім загальних принципів їх будівництва. Я також поговорю тут проекцій, формально звертаючись до координаційної довідкової системи, оскільки вона не має сенсу для карт цього масштабу до окремої проекції та дати. Тут немає математики, крім простої геометрії. Ті, хто бажає дізнатися про математичні принципи, можуть зробити це через статті на Wolfram MathWorld. Для студентів програмування в галузі геоінформаційних систем або їх досвідчених користувачів ця стаття не може бути дуже корисною.
Перед тим як почати, я поясню кілька речей. Всі приклади будуть надані за допомогою національних даних, що містяться в цьому сайті, і наведено на основі даних променевого покоління НАСА. Останні додані синтехічні зображення поверхні Землі для кожного з дванадцять місяців 2004 року, що дозволить отримати деякі різноманітні ілюстрації.
Я хотів відкрити програмне забезпечення дуже багато, але використовуючи GDAL в цьому випадку, здається неефективним для мене - деякі не дуже запущені, але корисні проекції в його реалізації в даний момент або не існує, або я не виглядав на вихідний код, і тому я підготували ілюстрації в комерційній програмі GlobalMapper, які я використовую протягом багатьох років, і які відомі для підтримки вражаючого списку координатних систем.
Я даю імена проекцій і деякі умови англійською мовою, тому що якщо хтось хоче шукати матеріали на цій темі, є кілька менш російськомовних джерел в мережі (кількість статей у Вікіпедії в Росії кілька разів менше). Для більшості проекцій я спробую дати не тільки імена, але й коди EPSG та/або WKID, а також назву проекції в бібліотеці PROJ.4, широко використовується в програмному забезпеченні відкритого джерела (наприклад, пакет R) для підтримки координатних систем.
Деякі проекції можуть бути знайомі з кимось з картинки xkcd, але всі вони не будуть розглянуті тут.
Почнемо з тим, що найбільш поширені проекції, і що їх неправильно.
Географія проекції, Latitude/Longitude, Plate carrée EPSG:4326 WKID:54001 PROJ.4:longlat. Строго кажучи, це не зовсім проекція, оскільки вона виходить шляхом інтерпретації полярних кутових координат як лінійних прямокутних координат, без будь-яких обчислень. Ця проекція використовується тому, що вона здатна відображати всю поверхню Землі і тому, що це найпростіше математично, і дані дуже часто пропаговані непроектовані, тобто в географічних координатих (відчуття широтності і довготи).

Що відбувається? Виявляється прямокутник, де фіксуються стовпні точки в лініях (верхова та нижча гра). Далі від еквалайзера, більш міцний будь-який об'єкт на карті, вирівнюється вертикально і простягається горизонтально. Як я сказав, що це досить добре для відображення глобальних даних, але полярні території (Канада, Норвегія, Швеція, північна Росія, Фінляндія, Грінланд, Антарктика, Ісландія) спотворюються. Проекції, які не можуть бути обговорені пізніше. Єдина причина використання цієї проекції є її екстремальною простотою впровадження програмного забезпечення - вам просто потрібно на карті координатної системи від -180o до 180o до X і від -90o до 90o до Y до площини, враховуючи лінійні кутові одиниці.
Ще один популярний проекція мерця PROJ.4:merc. Він також використовується для візуалізації даних, що охоплюють весь світ, але його популярність диктується не тільки простотою - його варіанти є дефакто стандартом для глобальних картографічних послуг, таких як Google Maps, Bing Maps, тут. Він глибоко пов'язаний з бібліотекою OpenLayers, Leaflet, API вищевказаних сервісів. У варіанті Google і OpenStreetMap він називається Web Mercator і має код EPSG / WKID:3857, іноді також називають EPSG:900913. Принцип його побудови не набагато складніший, ніж географічний - це проекція на циліндрі, вісь якого збігається з географічною віссю Землі, проекція виникає по лініях, що залишають центр планети, з яких похибка розтягування окружних регіонів горизонтально компенсується пропорційним розтягуванням по вертикалі. Єдина проблема з цим є те, що карта занадто велика вертикально, якщо ви намагаєтеся на карті на північ від Greenland. Таким чином, 16° полярних регіонів зазвичай викидаються (в рівній пропорції або більше з півдня).

У деяких очах людей виглядає трохи краще, ніж Географічна, але одна проблема вже згадувала, а другий - тим, що чим ближче об'єкт до стовпів, тим більше він з'являється, хоча його форма не так спотворюється. Таким чином, якщо об'єкт візуалізації є щільність маркерів на одиницю території або відстані, цей метод відображення буде вводитися в оману. З грамотним вибором способу візуалізації, звичайно, це можна компенсувати, і для деяких випадків це не проблема на всіх: наприклад, якщо значення деякого показника в всій країні корелюється з кольором цієї країни на карті, ефект розтягування ділянки не впливає. Ця проекція зберігає лише форму об'єктів, тому намітки материків і країн досить визнаються. І як я сказав, що це ваш перший і простий варіант при створенні інтерактивних веб-карт.
Що робити з глобальними даними, якщо з якихось причин нам необхідно проекція, яка краще зберігає властивості об'єктів, таких як форма, площа, відстані та кути? Закони геометрії не дозволяють зберегти всі ці властивості одночасно, розгортаючи круглу поверхню Землі на площині. Однак для візуалізації даних, естетики та сприйняття є найважливішими, а не збереження властивостей, як для навігації або виконання завдань. Тому можна вибрати проекцію, в якій спотворення будуть рівномірно розподілені за властивостями. І є досить багато таких проекцій. Є три найвідоміших, з схожими властивостями: Winkel Tripel WKID: 54042 PROJ.4:винтри, Проекція Робінсона WKID: 54030 PROJ.4:робін, Каврський проекція. Першими і останніми мають мінімальні візуальні спотвори, і дуже важко відрізняти їх без перегляду сітки, тому я даю ілюстрацію для Winkel Tripel, оскільки один я особисто схожий на найбільш.

Як виглядає опис цієї проекції в форматі ESRI WKT:
PROJCS["Robinson", GEOGCS["GCS_WGS_1984", DATUM["D_WGS84", SPHEROID["WGS84", 6378137,298.257223563], PRIMEM["Greenwich",0], UNIT["Degree", 0.017453292519943295] ], ПРОЕКТІЯ["Roson", PARAMETER["central_meridian",0], PARAMETER[false][false][false][false], UNIT[0]
Як легко побачити, хоча спотворення контурів і невелике збільшення площі країн до стовпів також спостерігаються, але це навіть не може бути порівняно з розтягуванням географічного проекції і пропорційним збільшенням проекції мерця.
Тут ви повинні зробити невеликий з'їзд і звернути увагу на те, що перегляд за замовчуванням цього проекції страждає від одного недоліку, що стосується інших глобальних проекцій. Справа в тому, що якщо центральний меридіан – лінія підключення північних і південних полюсів через центр карти (довга походження) – береться як нуль меридіан, то карта буде нарізана на 180-му. Але третина Чукотки буде на лівому краю карти, а дві третини праворуч. Щоб зробити карту більш красивою, ріжуча повинна бути десь навколо 169-го західного меридіанського східного острова Ратманова, для якого 11-й слід приймати як центральний. Ось ілюстрація того, що відбувається:

Ось модифікований опис в ESRI WKT:
PROJCS["Robinson", GEOGCS["GCS_WGS_1984", DATUM["D_WGS84", SPHEROID["WGS84", 6378137,298.257223563], PRIMEM["Greenwich",0], UNIT["Degree", 0.017453292519943295], ПРОЕКТІЯ["Roson"], PARAMETER["central_meridian",11], PARAMETER[false][feasting"false], PAth[0]
У форматі координатної системи для PROJ.4 довгота проекційного центру надається +лон_0=.
11-й меридіан – це «магічний» номер: майже всі світові проекції, які мають рівномірну вагу вздовж еквалатора, можна розрізати вздовж Берінгової протоки, якщо вона береться як центральний, так і не нульовий.
Зауважте, що придумці про вибір проекції варто враховувати всі існуючі реальні вимоги до візуалізації. Наприклад, якщо дані відносяться до клімату, це може бути сенсом або картою широтних ліній або використовувати проекцію, де вони горизонтальні, а не згинаються до країв карти (тобто відмовитися від Трійки Winkel на користь, наприклад, Робінсон). У цьому випадку це полегшить і більш точну оцінку відносної близькості від різних місць до стовпів і еквалатора. Ще одним значним плюсом проекції Робінсона є те, що він підтримує багато програмного забезпечення, в тому числі відкриті джерела, а деякі інші не можна сказати.

Іноді, коли необхідно зберегти деякі властивості якомога простіше, наприклад, співвідношення площі об'єктів (знижок) - естетична сторона страждає. Але оскільки це ще може знадобитися для чогось, я даю один приклад такої проекції – проекція Моллвейда WKID: 54009 PROJ.4:молл.

Як ви можете побачити, це досить схоже на проекцію Робінсона, але з різницею, що стовпи ще затягуються в точки, що робить форму окружних регіонів дуже спотворена. Але пропорції області країн, що вимагаються, значно краще зберігаються.
Наймолодший конкурент цих проекцій – природна ЗемляПРОЙ.4: проекція натур – це гібрид проекцій Кавражського та Робінсона, а його параметри були обрані групою американських, швейцарських та словенських фахівців у 2007 році, тоді як вік більшості картографічних проекцій не менше половини століття.

Є ряд інструментів, які були написані спеціально для цієї мети, але його підтримка далеко від ubiquitous.
Звичайно, всі проекції не закінчуються. Винайдено багато з них. Деякі просто дивляться дивні (са, проекція Bonnet зображує Землю як фігуру, що нагадує ріжучий яблуко або стилізоване серце), деякі призначені для спеціальних ситуацій. Наприклад, я б хотів би, що багато людей побачили карту світу в картинках, які виглядають як індинська скоринка, яка була видалена і плащена. Це, ймовірно, Goode's Interrupted Goode Homolosine projection WKID:54052.

Її зовнішній вигляд досить гідний назви. Його мета полягає в тому, щоб відображати розмір об'єктів (і в певній мірі форма) близько до природних пропорцій. Його головна проблема, крім свого імені і дивного зовнішнього вигляду, полягає в тому, що вибравши центральний меридіан, неможливо переконатися, що не великий шматок землі вирізається. Щось з переліку обов’язково постраждає: Грінланд, Ісландія, Чукотка, Аляска. Особисто, на мій погляд, легше надати окремі зображення країн, ніж використовувати таку карту, якщо ви не хочете стилізувати вашу роботу на середину XX століття.
Є проекції, які не є універсальними в природі, але я хотів би подивитися на них тут, тому що вони здатні показати світ, який є своєрідним виглядом планети з космосу. Вертикальний проекційний проекційний проекційний проект (WKID: 54049) Особливою властивістю є показати поверхню землі в такій перспективі, як вона виглядає з певної висоти. Висота над еліпсоїдом (ідеалізовані моделі фігури Землі) дається для цього проекції в явному вигляді.

У ілюстрації цей проекція має широту і довготу центру, що дорівнює широтості і довготи Москви, а висота 5000000 метрів. Чим більша ця відстань, тим сильніше зображення Землі стає схожим на його зображення в проекції ми розглянемо останнє.
Проекція, яка показує паралельний вигляд Землі з нескінченної відстані називається Ортографічним виступом WKID:43041 PROJ.4:ortho. Якщо ви не використовували Google Earth. Я кажу, що в сенсі, тому що "режим альтанки" в цьому проекції завжди перпендикулярно поверхні Землі, тоді як в Google Earth можна нахилити як вам подобається.

Для цього, як для попередньої проекції, можна вказати центральну широту і довготу, щоб орієнтуватися на Землю за бажаним способом. Наприклад, ви можете показати півсферу з центром в певній точці питання – наприклад, ілюструвати континентальні витрати трафіку, що генеруються з одного підприємства. Створення двох карт з протилежними координуючими значеннями, ви можете отримати карту усього світу (хоча по краях спотворення буде дуже великим). Створення послідовності карт з гладкою зміною в центральній точці дасть кадри для анімації обертальної планети без тривимірної графіки.
Якщо стаття доведе цікаве, я намагаюся писати про проекції, які використовуються для відображення окремих країн або регіонів, спрямованих на те, що ця стаття, на базових властивостях цих проекцій для задачі візуалізації даних, інфографіка та вподобання.
Джерело: habrahabr.ru/post/235283/