1361
Will science to improve the theory of music?

In my last article I discussed the question of how to build a music theory based on empirical observation < / a> for people - based on their tastes and musical preferences. Also for building musical theory can try to understand what is going on in our heads. This question is considered Wilkerson Daniel (Daniel Shawcross Wilkerson) in his article «harmony Explanation: On the way to the progress of scientific theory of music." This essay is a charming old-fashioned second name:
major scale, standardized terminology and differences in the perception of minor and major triads, which explains the basic principles of physics and mathematics. Refuting the Helmholtz and the justification theory Terhardta and other. B>
Wilkerson begins with remarks that books on music theory as read medical texts of the Middle Ages, and "they are full of unfounded judgments with fun characters, embellished phrases in Latin." We can write them clearer.
Wilkerson suggests that the theory of harmony is necessary to build an understanding of the brain, and in particular how it handles audio. In the course of our evolution, we have acquired the ability to recognize sounds with natural harmonics, because they usually come from the known sources can serve as an example of the pharynx other animals. Musical harmony - it invented their way to please us recognizers harmonic series.
How well can we perceive harmonic sound? So well that if we hear excerpts of several overtones, we can easily and completely unconsciously can supplement his absence overtones. For example, if we hear the harmonic series, which lacks the basic tone, we automatically adds them to the sequence. In particular, when we hear the harmony of several colors, we can calculate the greatest common divisor of their frequencies and assume its general tone. This phenomenon of "imaginary tone" makes it possible to distinguish between the bass line, listening to music in headphones tiny. Even though the speaker size is not large enough to play the bass, we extrapolate it from overtones.
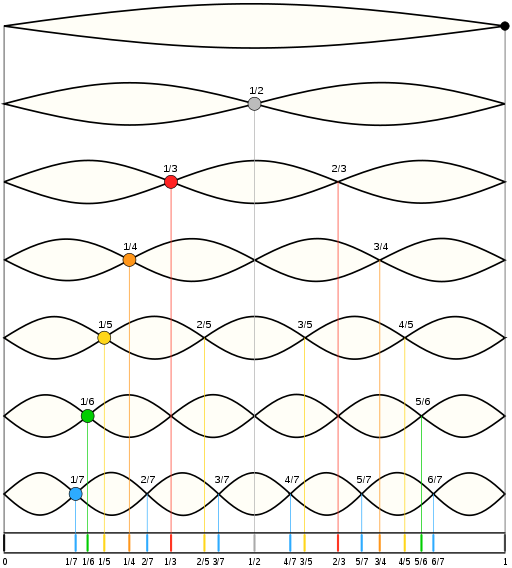
The idea is that our brain has special detectors harmonic series, which help distinguish equivalence octaves .
While various pitch harmonic series are different, the ratio of their frequencies to the fundamental frequency is always constant. Therefore, we believe that the brain performs normalization tones by their division and gets some of their relations. Audio processing required to analyze frequencies differing from each other by several orders of magnitude. If these frequencies can be completely analyzed, then we are able to re-use this knowledge. Consider conceptually simple process when the brain reduces or increases the frequency of the wave twice as long as the value does not fall within a certain range.
Now brain needs something to detect the harmonic series of tones in the frequency range not exceeding twice the tone, rather than the entire audio spectrum. Thus, the problem is broken down into two subtasks, where the first - this normalization, a second - a direct detection, which greatly simplifies the design of the resulting resolver. Therefore, we believe that it is likely our brain normalizes tone, halving or doubling them as long as they do not fall into a specific range of frequencies that differed by two orders of magnitude. Also, it is likely that the brain doubles or halves the frequency for various powers of two in parallel, and then spends their simultaneous detection. If any frequency is the same as [with base band], the desired harmonic found.
So why do we like harmony? Wilkerson says that it boils down to a series of artificially enhancing the natural overtones. Hear the chord - is like hearing a magical voice with a strong and clear harmonics than the individual [natural] sound source. Wilkerson once put it, that the harmony of our "sweet sweet».
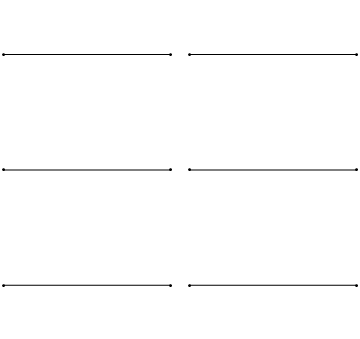
Below is an illustration of the fact that the mean Wilkerson. The figure shows a spectrogram of the two notes played on the violin: the note C ("before") on the left and G («G») on the right.
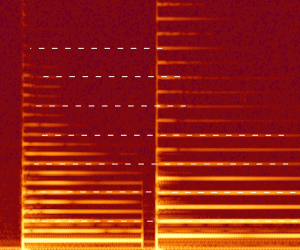
Dotted lines show the notes that are almost the same spectrum. Each overtone of C can be found in a similar note G. If you lose the notes at the same time, the harmonic resolver in your brain immediately activated and will mark a striking match.
This is a good explanation of consonance. But we also love and consonant harmony. Wilkerson thinks about this? He withdraws it on our innate love of narratives by comparing the sequence of chords with the plot works.
If we understand and predict the storyline of the story is fairly easy, the story seems boring, but if it is too difficult, then the story turns chaotic. If you keep the story between these two extremes, it turns out an interesting story. Simplicity comes from the "themes" of the story, its main idea, and ambiguity - is the lack of a simple explanation or "themes", causing difficulty.
Develop a theme at the beginning - a way to get rid of the complexity in the bud. Probably a branch of the themes and unexplained residual complexity "read" our brains with "handler expectations." The art of managing harmony - is, for the most part, just a game with the handler expectations when you give him so many difficulties that the initial information has remained an interesting area: between something obvious and somewhat meaningless.
Next, let's see what he thinks Wilkerson about how we obtain a simple diatonic harmony of the natural overtone series. We begin with a search for an ideal harmonic series consisting of a single note, say C4 - «to» the fourth octave ("before" the first octave on the piano) and correlate it with the entire octave by dividing the frequency as needed.
I will follow the conventions of Wilkerson and will assume the first harmonic of the fundamental:
The second harmonic has a frequency twice as large as the C4, C5 turns note - the "before" of the second octave. The third harmonic with a frequency of three times greater than C4 - a G5. When you divide its frequency by two, you get the G4 - perfect fifth "before" - "salt" of the first octave. The fourth harmonic with a frequency of four times the C4 - C6 is. In fact, all the even harmonics - it's just a note ("before"), transposed two octaves higher. The fifth harmonic with a frequency of five times the C4 - is E6. Normalize it, we E4 - major third "before" - "mi" of the first octave.
Further, Wilkerson asked us to build another major triad, based on a note in a series of overtones, closest to the fundamental tone. The first note you get harmonic notes C (not counting C an octave above) - is G («G»). If you build a major chord based on the notes G, you get the notes G, B and D («G", "B" and "D"). Wilkerson then wants us to build from the nearest major chord notes, which is the third harmonic of the note C. This note is F («fa") and its major chord is played in a series of overtones F, A and C («F», «la "and" to "). Rank all the notes in accordance with the frequency, you get the sequence C, D, E, F, G, A, B - that is, the well-known major scale .
Once you get this set of notes, you can deduce from them all kinds of other interesting chords and scales. Using the notes D, E or A («D", "E" or "A") as a basis, you will get a minor chords . Our emotional response to minor chords is more complicated than just "Aha!", As in the case of major recognition. Minor triad A («to" - "E" - "la") has the same pair intervals of the harmonic series: quint between A and E («A" and "E") and a major third between C and E. But we do not hear very harmonic series. Wilkerson believes that we find minor chords more interesting due to the fact that we know them only in part, and they tease our internal resolver harmonic series.
Subsequently, the theory reinforce the fact that there is only one major series, while the minor series set. I recall that in a major series, built from major triad, everything sounds clear to the human ear, while the sound of the minor series constructed from the minor chords often seems wrong and ambiguous.
On disambiguation spent a lot of our mental resources - is, in fact, the most likely search and logical explanation is vague and contradictory information about the world. In this we differ from computers and exceeds them in some situations. Music teases portion of our brain that is responsible for the resolution of ambiguous situations, causing us easily recognizable images with implicit values.
Wilkerson likens the complex harmony of drawings in the style of Cubism:
Part of the object can be displayed on a reasonable basis, so that they are easy to recognize, but the object as a whole is drawn unclear. An interesting effect: we recognize the object of individual features that catches our perception, but we still have a sense that we see the object is not in its natural form, and in the form of random, inappropriate or unclear.

What about the more complex chords? Wilkerson says that logic applies here, which we have used to explain the influence of minor chords.
The brain wants to hear a certain chord progression. If we "pass" [in our sequence] more and more music and the brain will try to fill more and more passes, then soon enough come a time when music is played barely enough to recognize the harmonic series. What if the played notes will not be sufficient to define it? Does this mean that the harmonic series gaps can be filled more than one way?
Some chords are ambiguous and therefore unstable. If the brain is more than one alternative fill the gaps, the sound will be "unstable" as long as the artist does not provide a sufficient number of notes that can "break the disparity" and a number of ambiguities.
If you hear the notes C, F and G («up", "F" and "G"), you hear something similar to some natural number of overtones. But which one? As C («up") and F («F») may serve as a pitch. Musicians call such situations "suspended chord" that pretty accurately describes the situation. You sort of in limbo between two permissible situations in which or C or F can act as basic notes. If we replace F by E («E»), the situation will be resolved in favor of C, while if G is replaced by A («A»), in favor of F. In more contemporary music, such a situation can not be resolved at all.
The idea of ambiguity perfectly explains any of the exotic chords. When you hear the increased or decreased triad or jazz chord with a lot of "extra" notes, you can hear the paired slots that are in tune with a number of overtones. But you do not hear the finished overtone series, and may hear more than one such series. The result gives less pleasure than the major chord, but it still sounds like something big, you just need to make an effort to understand what is happening.
Probably, the brain has a disambiguation module, which works in verbal communication, and in other situations, as is the case with music. Thus, despite the fact that the chords may sound strange individually musical theme, anticipating these chords can bring them some sense. Remember the standard structure of a joke: history (the creation of threads), and then highlight. Zest will not be funny without the context that gives us the story, but we associate itself with a twist is a joke, and not take into account the history that has made this joke possible.
Wilkerson theory and the classical theory of consistent standards that the harmonic series - the heart and soul of harmony. However, there are a few moments in which these theories diverge. For example, Wilkerson rejects quint circle as a method of achieving harmony, but does not reject anything that illuminates the principles of nature music.
Circle of fifths - this is a red herring, which does not allow people to understand harmony, to realize how good it sounds.
I really like the theory Uilkesona, but at one point he is seriously mistaken - talking about his analysis newt a >.
The notes C and F # («before" and "F-sharp") on the piano just awful. This interval is also called Triton, since the distance between C and F # - it is three whole tones (where the word "tone" is meant the distance of the two tones - a total of three colors - it's six semitones). We can analyze why this interval sounds so unstable: the relationship between the [frequency] F # and C does not match any harmonic harmonic series. This interval is deservedly got its name "Devil's interval».
Wilkerson did a great job to protect their views on the influence of Eurocentric music cultivation, but here he allowed himself to deviate. Those of us who love the blues and his musical heirs, no sound will be called triton terrible. The sound, of course, is not so pleasant, like a fifth or a major third, but a little less pleasant sound - does not mean bad. Wilkerson could explain better newt, resorting to their own ideas about the ambiguity and complexity. Triton - a more "adult" sound, and it can not be found in a number of overtones, but can easily be obtained from the range that can be there. In C major, there newt between F and B («F» and «B»).
As one of the many musical theorists, Wilkerson has a lot to say about harmony and says almost nothing about rhythm. But he can be found here, this wonderful little paragraph:
Recently, listening to the night sounds of insects, I was struck by how they appear rhythm as "layering" fading musical "themes" to a new, more complex sequence of sounds. At first I heard a simple predictable rhythm, and suddenly, contrary to expectations, the rhythm changed, sounded "on top" of the main theme. Phenomenon narrative, forecasting and prediction theme can be attributed to both the harmony and the rhythm. The phenomenon of expectations as it summarizes the input data, and therefore the expectation of harmony should work in a similar manner with rhythmic expectation.
Harmony - an idealized abstraction of the human voice and the rhythm - the idealized abstraction of physical movements, dancing. I would like to promote the theory Wilkerson step further. Note - it's just a very fast rhythm and chords - this is a very fast polyrhythms. As the rhythm is the foundation of music in general, and our theory rate shall be the basis of our theory of music.
Source: geektimes.ru/company/audiomania/blog/245532/