Чи може наука поліпшити теорію музики?

У своїй останній статті я обговорював питання, як побудувати музичну теорію на основі емпіричного спостереження людей на основі своїх смаків і музичних вподобань. Також, щоб побудувати музичну теорію, ми можемо намагатися зрозуміти, що відбувається на наших головах. Дане питання було адресовано Данилом Шавросом Вілксоном у своїй статті, «Розкриття Гармонії». Прогрес Towards в науковій теорії музики. Цей есе має другий чарівний старомодний титул:

Основні масштаби, стандартна термінологія та відмінності у сприйнятті неповнолітнього та великого тріаду, які пояснюються базовими принципами фізики та математики. Невідповідність теорії Гальмхолця, а також обґрунтування теорії Терхардта та інших.

Відповідає, що книги з теорії музики читати як медичні тексти Середньовіччя та «заповнювати необґрунтовані судові рішення з амузійними символами, прикрашеними фразами латинської мови». Ми можемо писати їх більш чітко.



Wilkerson пропонує, що теорія гармонії повинна бути побудована на розумінні, як працює мозок, і зокрема, як він обробляє звукові сигнали. В ході нашої еволюції ми придбали можливість розпізнати звуки з натуральними гармоніками, оскільки вони зазвичай приходять з джерел, відомих нам, таких як горла інших тварин. Музична гармонія – це шлях, який ми придумали, що наші гармоніки серії.

Як добре можна сприймати гармоніку звуку? Так само, якщо ми чуємо проходи серії надтонів, ми можемо легко і несвідомо доповнювати його відсутніми перегонами. Наприклад, якщо ми чуємо гармонічні серії, які не вистачає базового тону, ми автоматично додаємо послідовність до неї. Зокрема, коли ми чуємо конзонанс декількох тонів, ми можемо розрахувати найбільш поширений дивізор їх частот і розглянемо його загальний тон. Це явище «імагнітного тону» дає можливість відрізнити басову частину, слухаючи музику в крихітних навушниках. Незважаючи на те, що розмір динаміка недостатньо для відтворення басу, ми екстраполювати його з перегонів.

199099Р.

Ідея полягає в тому, що наші мозки мають спеціальні гармонічні детектори серії, які допомагають відрізняти рівновагу восьминапів.

Незважаючи на те, що значення різних гармонічних рядів відрізняється, співвідношення їх частот до базової частоти залишається постійним. Тому ми вважаємо, що мозок нормалізує тони, розділяючи їх і отримує деякі їх співвідношення. Звукова обробка вимагає аналізу частот, які відрізняються декількома замовленнями величини. Якщо ці частоти можна повністю проаналізувати, то ми можемо повторно використовувати ці знання. Розглянемо концептуально простий процес, де мозок знижує або подвоює частоту хвилі, поки вона потрапляє в певну діапазон.

Тепер мозок потребує чого розпізнати тони гармонічної серії в діапазоні частот, які не перевищують тон двічі, а не весь звуковий спектр. Таким чином, проблема ділиться на два підзаки, де перша нормалізація, а другий — безпосередньо визнання, що значно спрощує оформлення отриманого розпізнавання. Отже, ми думаємо, що наш мозок нормалізує тони шляхом халвінгу або допуску їх до тих пір, поки вони потрапляли в певну кількість частот, які варіюються на два замовлення. Імовірно, що мозок ділиться на пів або подвійних частотах на різні ступені зневоднення паралельно, а потім проводить одночасне визнання їх. Якщо в будь-яких частотних матчах [лінійний діапазон], знайдений бажаний гармонік.

Чому ми любимо гармонію? Wilkerson каже, що він відварює до штучно посилює природну серію надтонів. Зцілення акорду, як слухання магічного голосу з більш міцними і чистими гармоніками, ніж єдиний джерело звуку. Вінксон один раз сказав, що гармонія «солодка, ніж солодка. й

Нижче наведено ілюстрацію про те, що ознайомлений Wilkerson. На малюнку зображено спектрограму двох нот, які граються на скрипці: замітка C ("до") зліва і G ("сол") праворуч.



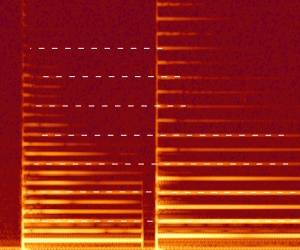
Дотовані лінії позначені ноти, які мають майже однаковий спектр. Кожна переробка C може бути знайдена схожа на G замітку. Якщо ви граєте ці ноти одночасно, гармонік визнає у вашому мозку відразу активує і відзначає вражаючий матч.

Це гарне пояснення для консонсу. Але ми також любимо невідповідні гармонії. Що таке Wilkerson? Він приписує це в нашу непристойну любов до розповіді, порівнюючи послідовність акордів до сюжету роботи.

Якщо ви зрозуміли і прогнозуєте сюжетну лінію сюжету досить легко, історія здається нудною, і якщо занадто складний, історія виходить плутати. Якщо ви тримаєте ділянку між цими двома крайами, ви отримаєте цікавий сюжет. Симплічність походить від «тема» сюжету, його головна ідея, а неоднозначність – відсутність простого пояснення або «тема», що викликає труднощі.

Відкриваючи тему на самому початку - це спосіб позбутися складності в бутоні. Ми можемо самі зателефонувати одержувачу і узгодити зручний час. Мистецтво управління гармонією є, для самої частини, просто граючи з обробником очікування, де ви даєте це стільки складності, що початкова інформація залишається в цікавій зоні: між чимось очевидним і чимось незначним.

Далі побачимо, що Wilkerson думає про те, як ми отримуємо просту діатонічну гармонію з натуральної серії надтонів. Ми починаємо пошук ідеальної гармонічної серії, що складається з однієї замітки, скажімо C4 – “before” четвертий окттав (“before” перший воктав на фортепіано) і доводите до всього вівця шляхом поділу частоти в міру необхідності.

Я буду дотримуватися конвенцій Wilkerson і розглянемо перші гармонічні основи.

• Друга гармоніка має частоту двічі, як високо, як C4, отримана замітка C5 – «до» другого октава.
• Третій гармонік з частотою три рази більше, ніж C4 є G5. Коли ви розділяєте свою частоту двома, ви отримуєте G4, чистий до-сольовий квінфік першого октава.
• Четвертий гармонік з частотою чотири рази більше, ніж C4 є C6. По суті, всі навіть гармоніки – це просто C ("до") замітка, що перекладається на два восьмикутники вище.
• П'ятий гармонік з частотою в п'ять разів більше, ніж C4 є E6. Ми отримуємо E4 – великий термін “before” – “mi” першого октава.

Отже, в першу чергу кілька природних гармонік містять велику третину і ноти C, E, G («до», «мі», «солод»), а також замітка «до», що перекладається на кілька восьмикутників. Якщо ви обираєте ще один гармонічний, як фундаментальний, ви отримаєте однакові співвідношення між частотами.

Далі Wilkerson попросить нас будувати ще одну основну тріду на основі замітки в серії перегонів, близьких до основного тону. Перша замітка, яку ви отримуєте від гармоніки C замітки (не підрахунку C октава вище) є G ("солити"). Якщо ви побудуєте основну тріду на основі G замітки, ви отримаєте ноти G, B і D («соль», «си» і «ре»). Після того, як ми хочемо, щоб побудувати велику тріду від найближчої замітки, де третій гармонік є заміткою C. Ця замітка F ("fa") і її головна тріада відтворена з серії надтонів F, A і C ("fa", "la" і "do"). Ви отримуєте послідовність C, D, E, F, G, A, B - це, добре відомий великий масштаб.

Після того, як ви отримаєте цей набір нот, ви можете вивести всі види інших цікавих акордів і масштабів з них. Використання нот D, E або A ("re", "mi" або "la") як основа, ви отримуєте незначні тринадцяти. Наша емоційна відповідь на неповнолітніх акордів є більш складним, ніж просто "Ага!", оскільки це справа з великим визнанням. Мінор тріад А ("до"-"mi"-"la") має однакові паровані інтервали гармонічної серії: хінта між А і Е ( "la" і "mi") і великою тирією між С і Е. Але ми не чуємо самі гармонічні серії. Волксон вважає, що ми знаходимо менші акорди більш цікавими, оскільки ми тільки частково визнаємо їх, і вони дражають наш внутрішній гармонічний серій.

Згодом теорія була підтримана тим, що існує лише одна велика серія, в той час як є багато незначних серій. Нагадуємо, що в основній серії, побудованій з великої трійці, все добре звучить до вуха людини, при цьому звук неповних рядків, побудований з неповнолітнього тріаду, часто здається неправильним і неоднозначним.

Великою угодою наших психічних ресурсів є усунення неоднозначності – в суть, є пошук найбільш ймовірних і логічних пояснень для вагової і суперечливої інформації про світ. В цьому випадку ми відрізняємося від комп'ютерів і перевершуємо їх в деяких ситуаціях. Музика дражає частину нашого мозку, відповідального за розв’язання неоднорідних ситуацій, викликаючи нас легко впізнавані зображення з неодружнім значенням.

Дільксон любить комплексну гармонію з кубиками:

Частини об'єкта можна зобразити досить надійно, тому що вони легко розпізнати, але об'єкт в цілому намальовується неперевершено. Цікавий ефект виникає: ми визнаємо об'єкт індивідуальними особливостями, які наше сприйняття захоплює, але ми все одно маємо відчуття, що ми бачимо об'єкт не у своїй природній формі, але у вигляді брудних, непристойних або неясних.

Габаритний зображення

Що про більш складні акорди? Wilkerson каже, що логіка, яку ми використовували для пояснення впливу неповних акордів.

Мозок хоче почути певну гармонічну послідовність. Якщо ми пропускаємо більше і більше нот [в нашій послідовності], і мозок намагається заповнювати більше і більше проміжків, то незабаром буде достатньо місця, коли відтворені ноти буде досить важко розпізнати гармонічний ряд. Що робити, якщо відіграли ноти не достатньо? Це означає, що проміжки в гармонічній серії можуть бути заповнені більш ніж одним способом?

Деякі акорди є неоднорідними і тому нестабільними. Якщо мозок має більше одного альтернативного варіанту, щоб заповнювати проміжки, звук буде «розкладним» до тих пір, поки виконавець забезпечує достатні ноти «розриву диспропорції» і неоднозначності серії.

Якщо ви почуєте ноти C, F і G ("до", "fa" і "солод"), ви почуєте щось схоже на деякі природні серії надтонів. Але що? І C ("до") і F ("fa") може діяти як основний тон. Музиканти називають такі ситуації, як «підготовлений акорд», що досить точно описує ситуацію. Ви сортуєте в кінцівці між двома дійсними ситуаціями, в яких може діяти як первинні ноти. Якщо F замінюється E ("mi"), ситуація буде вирішена на користь C, і якщо G замінюється A ("la"), то на користь Ф. У більш сучасну музику ця ситуація не може бути вирішена на всіх.

Ідея неоднозначності прекрасно пояснює будь-який з екзотичних акордів. Якщо ви почуєте розширений або зменшений тріад або джазовий акорд з багатьма нотами «екстра», ви почуєте парні інтервали, які співзвучні з рядом надтонів. Але ви не почуєте готову серію надтонів, і ви можете почути більше одного. Результат менш веселий, ніж великий акорд, але він все ще звучить як щось значне, ви просто повинні зробити зусилля, щоб зрозуміти, що відбувається.

Мозок, ймовірно, має один модуль роздільної здатності, який працює як у словесному спілкуванні, так і в інших ситуаціях, як у випадку музики. Отже, в той час як акорди можуть звучати дивний індивідуально, музична тема, яка передує ці акорди, може принести до них деяке значення. Пам'ятайте стандартну структуру жарту: історія (відтворення теми) і потім родзинку. Зест не смішний без контексту, що історія дає нам, але ми зв'язуємо самі жарти з гніздом, і не враховуємо історію, що зробив цей жарт можливо.

Теорія Вілксона і стандарти класичної теорії згодні, що гармонічна серія – серце і душа гармонії. Але є кілька точок, де ці теорії дивляться. Наприклад, Wilkerson відхиляє коло як метод досягнення гармонії, але не відхиляє все, що висвітлює принципи природи музики.

The Quintus Circle – це відволікання, що запобігає гармонії розуму, розуміючи, наскільки добре вона звучить.

Я дуже люблю теорію Wilkeson, але він неправильно про його новий аналіз.

Звук нот C і F# ("до" і "fa-sharp") на фортепіано просто страшний. Цей інтервал також називається новим, так як відстань між C і F# є трьома цілими тонами (де слово «тон» відноситься до відстані двох півтонів – разом з трьома тонами – шість половина тонів). Ми можемо проаналізувати, чому цей інтервал звучить так нестійке: відносини між частотами. F# і C не відповідають будь-якій гармонічній серії. Цей проміжок заслуговував на ім’я «відправлення».

Волксон зробив велику роботу з захопленням своїх поглядів від впливу євроцентричної музичної побуту, але тут він дозволив собі трохи відхиляти. Ті з нас, які люблять сині та його музичні спадкоємці, не зателефонують нове звучання страшним. Його звук, звичайно, не так приємно, як з хінта або великої третини, але трохи приємне звучання не означає погано. Дільксон може пояснити краще, використовуючи власні ідеї неоднозначності та складності. Тритон є більш "додатком" звуком, і він не може бути знайдений в серії надтонів, але можна легко отримати з інтервалу, який може бути там. У мажорі з’являється нове місце між Ф та Б («фа» та «сі».

Як один з багатьох музичних аортистів, Wilkerson має багато сказати про гармонію і майже нічого сказати про ритм. Ви можете знайти цей чудовий маленький пункт:

Увечері я захоплюю, як з'явився ритм, як захоплювальний музичний «тем» був шарований на нову, більш складну послідовність звуків. Спочатку я почув простий передбачуваний ритм, і раптом, навпаки, сподіваючись, що ритм змінив, звучаючи «понад» основну тему. Визначені явища оповідання, прогнозування та прогнозування теми можна віднести як до гармонії, так і ритму. феномен очікування підбиває вхідні дані, а отже, очікує гармонія повинна працювати аналогічним чином до ритмічного очікування.

Як гармонія – це ідеальна абстракція голосу людини, тому ритм – це ідеальна абстракція фізичних рухів і танців. Я хотів би взяти теорію Wilkerson ще крок. Замітка є дуже швидким ритмом, і акорди дуже швидко. Так само як ритм є основою музики в цілому, тому наша теорія ритму повинна бути основою нашої теорії музики.

Джерело: geektimes.ru/company/audiomania/blog/245532/