1576
Ідентифікація швидкої теплових процесів
Нещодавно я зумів завершити роботу над цікавим проектом FTI. Отримати достатню кількість експериментальних даних, щоб поділитися з вами.
Лікарі з Санкт-Петербурга. Іоффе займається вирощуванням нітридних жовчних напівпровідників, які мають хороші показники швидкості зарядних носіїв при переході і великим коефіцієнтом теплопровідності. Процес зростання такої структури відбувається при температурі 1000 С (1273 К) і атмосферному тиску. Все відбувається в спеціальній камері, розташованій в герметичній зоні. При вирощуванні конструкції весь обсяг реактора і запечена зона заповнюється азотом. Як росте структура, субстрат обертається один раз на другий. Такі операції відносяться до швидких теплових процесів, швидкість зміни температури, в яких варіюється від декількох одиниць до сотні градусів за секунду.
 р.
р.
Моє завдання було контролювати температуру графітової підкладки при індуктивному нагріванні.
Технічні характеристики установки: Для вимірювання температури використовується лазерний пірометр, який бере дані в центрі графіту. Частота видалення 10 разів на секунду, покрокове вимірювання 1 ступеня. Потужність передається графіту передбачається безпосередньо пропорційно потужності на індукторі. Генератор, що контролює індуктор, має цифровий вихід, через який передається напруга, струм і потужність.
Для початку необхідно регулювати регулятор температури, щоб не було сильного коливання в процесі росту. Це завдання було дуже швидко, але наше рішення дав якісний результат тільки при високих температурах. Для інших процесів коефіцієнти повинні бути змінені.
Так як ця робота вписана в тему кандидата, я хотів писати алгоритм керування кінніком на основі аналізу моделі термічного процесу. Для початку я познайомився з законом Стефана-Болцмана, променева потужність повністю чорного тіла безпосередньо пропорційна площі поверхні і четвертому ступені температури. Враховуючи конвекцію, можна написати рівняння для термічних процесів при температурі
де T - це температура, P - це потужність, Tc - це температура навколишніх об'єктів, які нагрівають графіт з власною радіацією, Ta - температура газу біля точки прийому інформації, яка виконує конвекцію, B, A1, A2 - коефіцієнти, які повинні бути виявлені. Щоб спростити, ми замінимо всі компоненти рівняння, які ми можемо розглянути постійний в встановленому процесі і розглянемо наступні рівняння.
У нас є модель, яку ми можемо побудувати, коли ми аналізуємо дані далі. У експерименті в якості сигналу задано означальник.
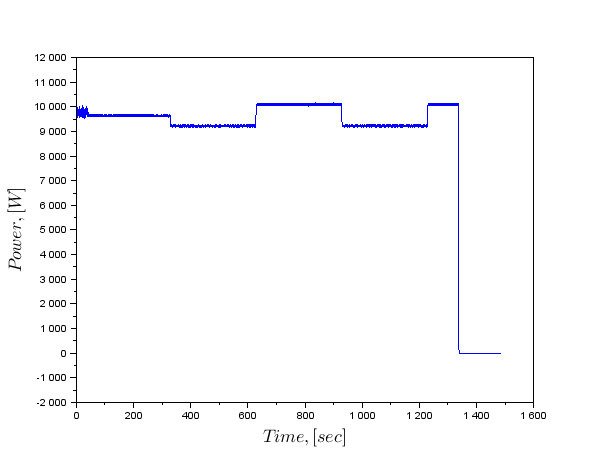
Якщо ми отримуємо оцінку швидкості температури, ми можемо зробити регресивну модель з відомою температурою і потужністю контрольного індуктора і розрахувати коефіцієнти в рівняння.
Я користуюсь Scilab протягом всього часу, і цей час я вирішив не обдурити. Для цього завдання я вирішив взяти похідну у вигляді Фур'є. Але почати працювати з реальними даними, потрібно переполювати вимірювання, щоб отримати рівномірну вісь часу.
Варто відзначити, що змінна "int_temp_diff" буде містити дані швидкості, але вони виглядають дуже неприємно.
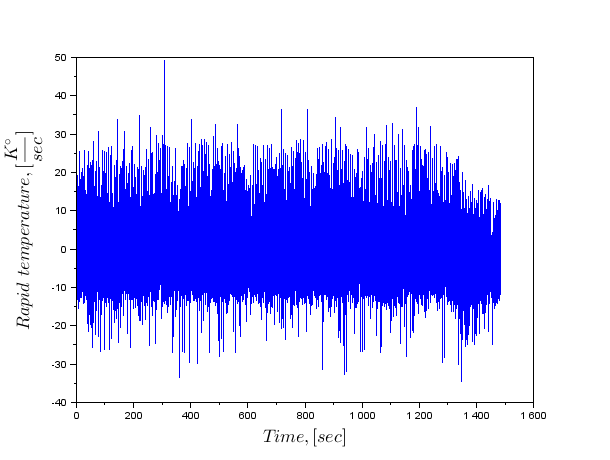
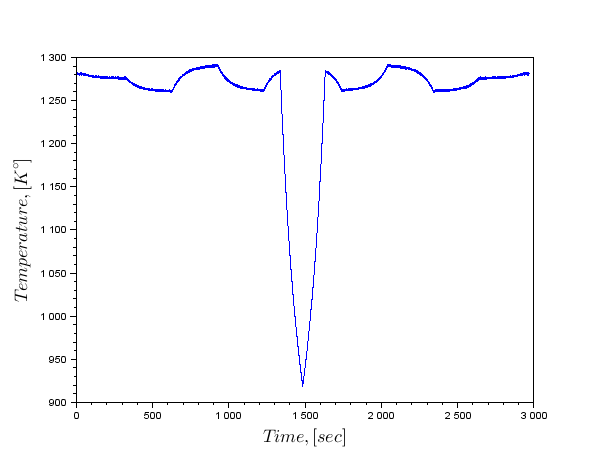
Таким чином, перейдемо на дані Фур'є. Для побудови додаткового хвостика даних не потрібно перерву в кінці, віддзеркалення графіка температурних даних.
 , доб. 114
, доб. 114
Потім ми встановлюємо частотну вісь і робимо дискретний трансформатор.

На частоті 1 гризу видно чіткий пік, це пов'язано з тим, що субстрат обертається з цією частотою. За рахунок того, що графіт нагрівається нерівномірно, а при обертанні температура може збільшитися і зменшити кілька разів.
Щоб взяти похідну в образ Фур'єра, потрібно лише помножити на. Потім ми робимо зворотну трансформацію Фур'єра.
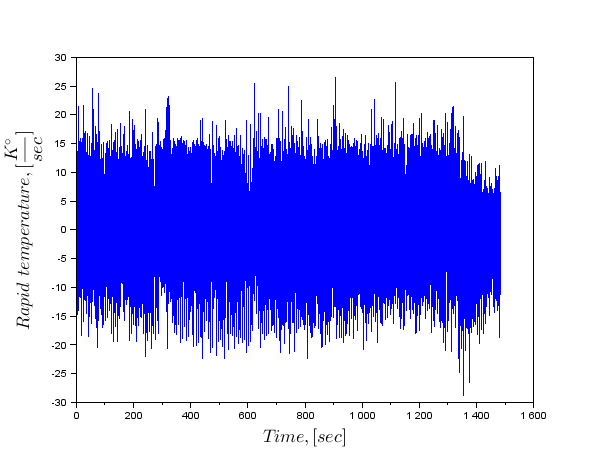
Це, безумовно, трохи краще, ніж що повертає функцію прийняття похідних через кубічні шпилі, але ідентифікація з цим дає низькі результати якості. Ви повинні фільтрувати сигнал.
На пораді мого друга Юри, який займається налаштуванням систем управління судном, було прийнято рішення використовувати вікно Blackman-Harris, щоб вирізати зайві частоти. Оскільки в процесі зростання графіт обертається при частоті 1 раз на секунду, всі коливання з частотою вище цього не цікаві. Тому варто розрізати всі коливання вище 1 [Хз]:
Лікарі з Санкт-Петербурга. Іоффе займається вирощуванням нітридних жовчних напівпровідників, які мають хороші показники швидкості зарядних носіїв при переході і великим коефіцієнтом теплопровідності. Процес зростання такої структури відбувається при температурі 1000 С (1273 К) і атмосферному тиску. Все відбувається в спеціальній камері, розташованій в герметичній зоні. При вирощуванні конструкції весь обсяг реактора і запечена зона заповнюється азотом. Як росте структура, субстрат обертається один раз на другий. Такі операції відносяться до швидких теплових процесів, швидкість зміни температури, в яких варіюється від декількох одиниць до сотні градусів за секунду.
 р.
р.Моє завдання було контролювати температуру графітової підкладки при індуктивному нагріванні.
Технічні характеристики установки: Для вимірювання температури використовується лазерний пірометр, який бере дані в центрі графіту. Частота видалення 10 разів на секунду, покрокове вимірювання 1 ступеня. Потужність передається графіту передбачається безпосередньо пропорційно потужності на індукторі. Генератор, що контролює індуктор, має цифровий вихід, через який передається напруга, струм і потужність.
Для початку необхідно регулювати регулятор температури, щоб не було сильного коливання в процесі росту. Це завдання було дуже швидко, але наше рішення дав якісний результат тільки при високих температурах. Для інших процесів коефіцієнти повинні бути змінені.
Так як ця робота вписана в тему кандидата, я хотів писати алгоритм керування кінніком на основі аналізу моделі термічного процесу. Для початку я познайомився з законом Стефана-Болцмана, променева потужність повністю чорного тіла безпосередньо пропорційна площі поверхні і четвертому ступені температури. Враховуючи конвекцію, можна написати рівняння для термічних процесів при температурі
де T - це температура, P - це потужність, Tc - це температура навколишніх об'єктів, які нагрівають графіт з власною радіацією, Ta - температура газу біля точки прийому інформації, яка виконує конвекцію, B, A1, A2 - коефіцієнти, які повинні бути виявлені. Щоб спростити, ми замінимо всі компоненти рівняння, які ми можемо розглянути постійний в встановленому процесі і розглянемо наступні рівняння.
У нас є модель, яку ми можемо побудувати, коли ми аналізуємо дані далі. У експерименті в якості сигналу задано означальник.

Якщо ми отримуємо оцінку швидкості температури, ми можемо зробити регресивну модель з відомою температурою і потужністю контрольного індуктора і розрахувати коефіцієнти в рівняння.
Я користуюсь Scilab протягом всього часу, і цей час я вирішив не обдурити. Для цього завдання я вирішив взяти похідну у вигляді Фур'є. Але почати працювати з реальними даними, потрібно переполювати вимірювання, щоб отримати рівномірну вісь часу.
xx = linspace(0, round(time($), round(time($))*fs+1)"; //Новий час осі ' d=splin(time,temp,"monotone"); [int_temp,int_temp_diff] = interp(xxxx, час, d); Варто відзначити, що змінна "int_temp_diff" буде містити дані швидкості, але вони виглядають дуже неприємно.

Таким чином, перейдемо на дані Фур'є. Для побудови додаткового хвостика даних не потрібно перерву в кінці, віддзеркалення графіка температурних даних.
 , доб. 114
, доб. 114Потім ми встановлюємо частотну вісь і робимо дискретний трансформатор.

fs = 10; // Частота в = [int_temp;int_temp($:-1:1)]; N = Довжина (в ); частота = [0 : (N-1)] / N * fs; частота (N/2+1 : $) = частота (N/2+1 : $) -fs; частота = частота = частота; sp = fft(в); //Fast Fourier Transform 519677На частоті 1 гризу видно чіткий пік, це пов'язано з тим, що субстрат обертається з цією частотою. За рахунок того, що графіт нагрівається нерівномірно, а при обертанні температура може збільшитися і зменшити кілька разів.
Щоб взяти похідну в образ Фур'єра, потрібно лише помножити на. Потім ми робимо зворотну трансформацію Фур'єра.
Омега = (2*%pi*%i* Частота); tmp = sp.*omega; з = реальний(fft(tmp,1)); швидкість_temp = вихід(1:N/2); 
Це, безумовно, трохи краще, ніж що повертає функцію прийняття похідних через кубічні шпилі, але ідентифікація з цим дає низькі результати якості. Ви повинні фільтрувати сигнал.
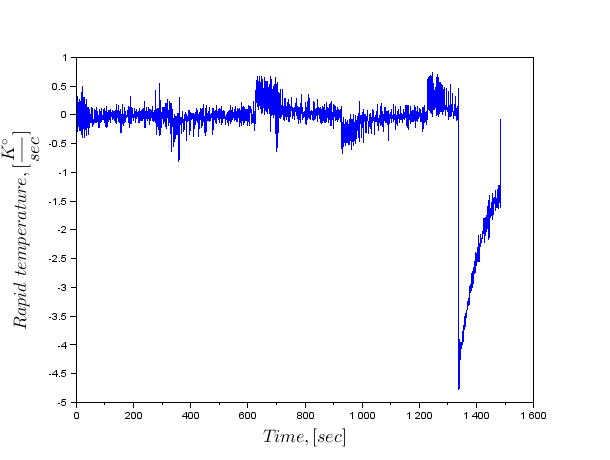
На пораді мого друга Юри, який займається налаштуванням систем управління судном, було прийнято рішення використовувати вікно Blackman-Harris, щоб вирізати зайві частоти. Оскільки в процесі зростання графіт обертається при частоті 1 раз на секунду, всі коливання з частотою вище цього не цікаві. Тому варто розрізати всі коливання вище 1 [Хз]:
cf = 1; // Частота вимкнення к = круглий(cf*N/fs); L = 2*k+1; a0=0.35875; a1=0.48829; a2=0.14128; a3=0.01168; для j=0:L-1, w(j+1) = a0 - a1*cos(2*%pi*j/(L-1))+a2*cos(4*%pi*j/(L-1)))-a3*cos(6*%pi*j/(L-1)); end h = нуль(частота); для j=kome=1=1=1
 р.
р.
Дуже добре. При цьому ми починаємо розрахувати коефіцієнти з'єднання.
Щоб отримати хороші дані, необхідно попередньо занурювати вектори даних. Для безкоштовної константи в рівняння потрібно вказати вектор, наповнений блоками.
констант (1: довжина(int_power)) = 1; норма_4_temp = норма(int_temp.^4); норма_int_temp = норма(int_temp); норма_int_power = норма(int_power); норма_speed_temp = норма(speed_temp); норма_constant = норма(constant);
Тепер ми можемо розпочати пошук значень констанцій. Зробіть матрицю, що містить значення трьох змінних і констанцій. Ми ділимо кожен вектор даних за його довжиною. Для отримання коефіцієнтів необхідно помножити матрицю псевдореверсу за допомогою нормалізованого вектора даних швидкості температур.
LSM = [int_temp.^4/norm_4_temp , int_temp/norm_int_temp , int_power/norm_int_power , постійний/norm_constant ] ; a0 = pinv(LSM) *speed_temp / норма_speed_temp ;
А потім необхідно повернутися до початкових значень коефіцієнта вектора.
a0(1) = a0(1) *norm_speed_temp/norm_4_temp; a0(2)*norm_speed_temp/norm_int_temp; a0(3) = a0(3) *norm_speed_temp/norm_int_power; a0(4) *norm_speed_temp/norm_constant; Результатом є наступні значення a0 = [ - 1.073D-12, - 0.0029096, 0.0004617, 2.0969723], які досить близько до результату наших іноземних колег, хоча вони використовують лампу опалення.
Тепер ви можете почати перевірку результатів за отриманою моделлю. Ми використовуємо пакет віртуального моделювання Xcos Scilab. Оскільки у нас є диференціальне рівняння, що описує тепловий процес в реакторі, і всі коефіцієнти до нього, ми збираємо наступну схему.
63421.
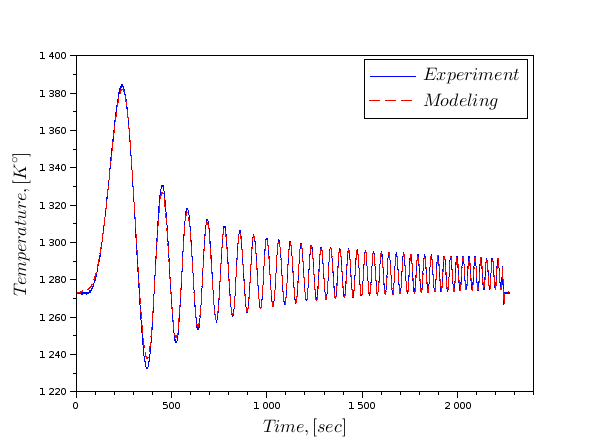
Блок «З робочого простору» забезпечує експериментальні дані живлення, які раніше створили структуру V для цього блоку. Встановіть частоту зразка і час, щоб розпочати моделювання в блокі "Clock". Довжина структури вихідних даних дорівнює вході. Час кінцевого моделювання повинен бути рівною до часу експерименту. Виконуємо складену модель в тексті програми та порівнюємо графіки експерименту та моделювання.
V.time = xx; V.values = int_power; importXcosDiagram("D:\PhD\Term_model.zcos"); xcos_simulate(scs_m,4); ділянка(time,temp);(A.time,A.values,"r-"); 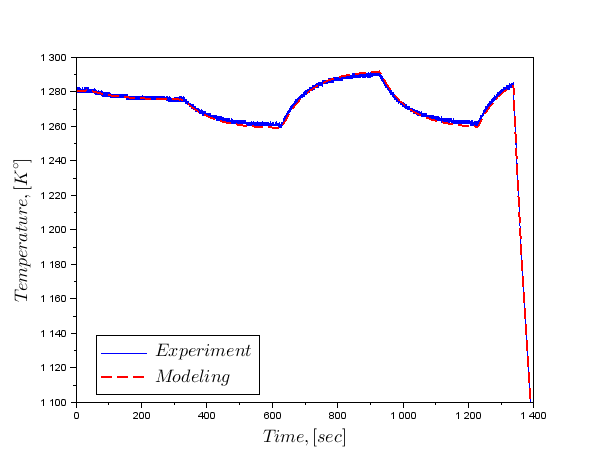
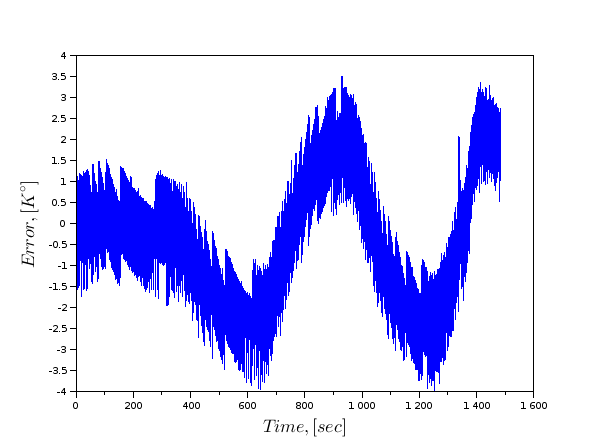
Ось те ж саме, але для гармонічного порушення з різною частотою.
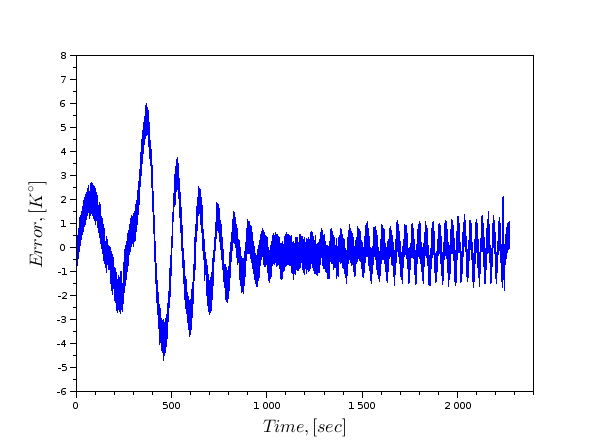
Велике спасибі науковому керівнику Араста за неоціненну допомогу і участь у підготовці матеріалу. Я подяку Євгену Заваріну за надання доступу до монтажу та впровадження програмного забезпечення всіх експериментів.
Джерело: habrahabr.ru/post/218297/
 р.
р.