1577
Identificación de los rápidos procesos térmicos
Recientemente tuve la oportunidad de completar el trabajo en un proyecto muy interesante en el Instituto Ioffe. Joffe y obtener suficientes datos experimentales para compartir con ustedes.
Física de San Petersburgo Instituto Ioffe. Ioffe dedica a crecientes estructuras de semiconductores de nitruro de galio, que tienen buena velocidad de rendimiento de los portadores de carga en la transición y una gran conductividad térmica. El proceso de crecimiento de esta estructura se lleva a cabo a una temperatura de 1000 C (1273 K) y presión atmosférica. Todo tiene lugar en una cámara especial situado en una zona de sellado. Cuando el crecimiento de la estructura y todo el volumen del reactor lleno con nitrógeno, se selló la zona. Durante el crecimiento de la estructura del soporte de sustrato se hace girar a una velocidad de una vez por segundo. Tal operación se refiere a los procesos térmicos rápidos, la velocidad de cambio de temperatura que va desde unos pocos a cientos de grados por segundo.

Mi tarea consistía en controlar la temperatura del soporte de sustrato de grafito mediante calentamiento inductivo.
Características técnicas son las siguientes. Para la medición de la temperatura, un termómetro láser, la eliminación de los datos en el centro de la grafito. La frecuencia de recuperación de información 10 veces por segundo, que miden el paso 1 grado. El valor de la potencia transmitida de grafito se basa directamente proporcional a la potencia del inductor. En el inductor de control del generador tiene una salida digital, que lleva a la tensión, corriente y potencia.
Para empezar, era necesario ajustar el control de temperatura en el proceso de crecimiento no ha sido fluctuaciones fuertes. Hecho frente a esta tarea con la suficiente rapidez, pero nuestra decisión de dar resultados de alta calidad sólo a altas temperaturas. Para otros procesos necesarios para cambiar los coeficientes.
Desde este trabajo encaja en el tema de mi tesis doctoral, que quería escribir algún algoritmo de control inteligente basado en el análisis del modelo de procesos térmicos. Para empezar familiarizarse con la ley Stefan - Boltzmann , radiación de cuerpo negro de potencia es directamente proporcional al área de superficie y el cuarto grados de temperatura. En vista de la convección puede escribir una ecuación para procesos térmicos en
eliminación temperaturas
donde T - temperatura, P - poder, Tc - temperatura de los objetos que lo rodean, que son calentados por el propio grafito radiación, Ta - temperatura del gas cerca de la recuperación de información de puntos que realiza por convección, B, A1, A2 - los coeficientes a ser identificado. Para simplificar reemplazar todos los componentes de la ecuación, que puede considerarse constante en el proceso constante y considerar la siguiente ecuación
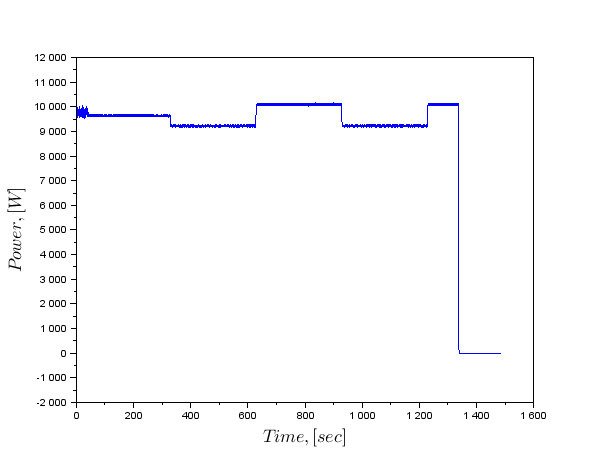
Ahora tenemos disponible un modelo del que empujar en un nuevo análisis de los datos. En el experimento, la señal alimenta a deambular.
Si se obtiene una estimación de la tasa de la temperatura, será posible hacer un modelo de regresión con conocido temperatura y control de potencia del inductor, y calcular los coeficientes en la ecuación.
Durante mucho tiempo he estado usando para Scilab y esta vez decidí no cambiar sebe.Dlya esta tarea Elegí la derivación en forma de series de Fourier. Pero para empezar a trabajar con datos reales, es necesario interpolar la medición para obtener un eje de tiempo uniforme.
Física de San Petersburgo Instituto Ioffe. Ioffe dedica a crecientes estructuras de semiconductores de nitruro de galio, que tienen buena velocidad de rendimiento de los portadores de carga en la transición y una gran conductividad térmica. El proceso de crecimiento de esta estructura se lleva a cabo a una temperatura de 1000 C (1273 K) y presión atmosférica. Todo tiene lugar en una cámara especial situado en una zona de sellado. Cuando el crecimiento de la estructura y todo el volumen del reactor lleno con nitrógeno, se selló la zona. Durante el crecimiento de la estructura del soporte de sustrato se hace girar a una velocidad de una vez por segundo. Tal operación se refiere a los procesos térmicos rápidos, la velocidad de cambio de temperatura que va desde unos pocos a cientos de grados por segundo.

Mi tarea consistía en controlar la temperatura del soporte de sustrato de grafito mediante calentamiento inductivo.
Características técnicas son las siguientes. Para la medición de la temperatura, un termómetro láser, la eliminación de los datos en el centro de la grafito. La frecuencia de recuperación de información 10 veces por segundo, que miden el paso 1 grado. El valor de la potencia transmitida de grafito se basa directamente proporcional a la potencia del inductor. En el inductor de control del generador tiene una salida digital, que lleva a la tensión, corriente y potencia.
Para empezar, era necesario ajustar el control de temperatura en el proceso de crecimiento no ha sido fluctuaciones fuertes. Hecho frente a esta tarea con la suficiente rapidez, pero nuestra decisión de dar resultados de alta calidad sólo a altas temperaturas. Para otros procesos necesarios para cambiar los coeficientes.
Desde este trabajo encaja en el tema de mi tesis doctoral, que quería escribir algún algoritmo de control inteligente basado en el análisis del modelo de procesos térmicos. Para empezar familiarizarse con la ley Stefan - Boltzmann , radiación de cuerpo negro de potencia es directamente proporcional al área de superficie y el cuarto grados de temperatura. En vista de la convección puede escribir una ecuación para procesos térmicos en
eliminación temperaturas
donde T - temperatura, P - poder, Tc - temperatura de los objetos que lo rodean, que son calentados por el propio grafito radiación, Ta - temperatura del gas cerca de la recuperación de información de puntos que realiza por convección, B, A1, A2 - los coeficientes a ser identificado. Para simplificar reemplazar todos los componentes de la ecuación, que puede considerarse constante en el proceso constante y considerar la siguiente ecuación
Ahora tenemos disponible un modelo del que empujar en un nuevo análisis de los datos. En el experimento, la señal alimenta a deambular.

Si se obtiene una estimación de la tasa de la temperatura, será posible hacer un modelo de regresión con conocido temperatura y control de potencia del inductor, y calcular los coeficientes en la ecuación.
Durante mucho tiempo he estado usando para Scilab y esta vez decidí no cambiar sebe.Dlya esta tarea Elegí la derivación en forma de series de Fourier. Pero para empezar a trabajar con datos reales, es necesario interpolar la medición para obtener un eje de tiempo uniforme.
& lt; code class = & quot; MATLAB & quot; & gt; xx = linspace (0, redondo (hora ($)), redonda (hora ($)) * fs + 1) '; // Nueva d = splin ejes Time '(tiempo, temperatura, & quot; monótona & quot;); [Int_temp, int_temp_diff] = interp (xx, tiempo, temperatura, d); & Lt; / código de & gt; pre>
Vale la pena señalar que la variable «int_temp_diff» contendrá la velocidad de datos, pero se ven muy no muestra parcialidad.
Así que manos a la obra con los datos en forma de series de Fourier. Tendremos que construir una cola de datos adicional que al final no hubo descanso, los datos de temperatura rotafolio.
Luego pida el eje de frecuencias y hacer transformada de Fourier discreta.
& lt; code class = & quot; MATLAB & quot; & gt; fs = 10; // Frecuencia de muestreo en = [int_temp; int_temp ($: - 1: 1)]; N = longitud (en); frecuencia = [0: (N-1)] / N * fs; frecuencia (N / 2 + 1: $) = frecuencia (N / 2 + 1: $) Fs; Frecuencia = frecuencia "; sp = fft (in); // Fast Fourier Transform & lt; / código de & gt; pre>
A una frecuencia de 1 Hz se puede ver un pico claro es debido al hecho de que el soporte de sustrato se hace girar con esta frecuencia. Otro frecuencia de muestreo debido al hecho de que el grafito se calienta de manera desigual y cuando la temperatura de rotación se puede aumentar y redujo varias veces.
Para tomar la derivada de la transformada de Fourier, simplemente multiplique por. Después de eso, haga lo transformada de Fourier inversa.
& lt; code class = & quot; MATLAB & quot; & gt; omega = (2 *% pi *% i * frecuencia); tmp = sp * omega.; a = real (fft (tmp, 1)); speed_temp = a (1: N / 2); & Lt; / código de & gt; pre>
Esto es, por supuesto, un poco mejor que el devuelto por derivación a través de splines cúbicos, pero la identificación de este número subestándar resultados. Tener que recurrir a la señal de filtrado.
Por consejo de mi amigo Jura, que se ocupa de la creación de sistemas de control de la nave, se decidió utilizar una ventana Blackman-Harris cortar frecuencia innecesaria . Dado que en el proceso de crecimiento gráfico gira con una frecuencia de 1 vez por segundo, todas las oscilaciones con una frecuencia superior a la que no están interesados. Por lo tanto, es necesario cortar todas las fluctuaciones por encima de 1 [Hz]:
& lt; code class = & quot; MATLAB & quot; & gt; cf = 1; // Frecuencia de corte k = round (cf * N / fs); L = 2 * k + 1; a0 = 0,35875; a1 = 0,48829; a2 = 0,14128; a3 = 0,01168; para j = 0: L-1, w (j + 1) = a0 - a1 * cos (2 * pi * j% / (L-1)) + a2 * cos (4 *% pi * j / (L- 1)) - a3 * cos (6 *% pi * j / (L-1)); final h = ceros (frecuencia); para j = 1: 1: k + 1 h (j) = w (k + j); final h ([$: - 1: $ - k]) = h ([1: 1: k + 1]); omega = (2 *% pi *% i * frecuencia); . omega = omega * h; tmp = sp * omega.; a = real (fft (tmp, 1)); speed_temp = a (1: N / 2); & Lt; / código de & gt; pre>
Se convirtió en mucho mejor. Con este comienzo al cálculo de los coeficientes de regresión.
Para obtener buenos datos, debe primero ser datos vectoriales normalizados. Durante constantes libres en la ecuación debe especificar unidades vectoriales llenas.
& lt; code class = & quot; MATLAB & quot; & gt; constante (1: longitud (int_power)) = 1; norm_4_temp = norma (. int_temp ^ 4); norm_int_temp = norma (int_temp); norm_int_power = norma (int_power); norm_speed_temp = norma (speed_temp); norm_constant = norma (constante); & Lt; / código de & gt; pre>
Ahora ya está listo para encontrar los valores de las constantes. Componente de una matriz que contiene los valores de las tres variables y constantes. En este dividir cada uno de los vectores de datos por su longitud. Para los coeficientes debe multiplicarse matriz pseudoinversa para una velocidad de datos vector normalizado de cambio de temperatura.
& lt; code class = & quot; MATLAB & quot; & gt; LSM = [int_temp ^ 4 / norm_4_temp, int_temp / norm_int_temp, int_power / norm_int_power, constante / norm_constant.]; a0 = Pinv (LSM) * speed_temp / norm_speed_temp; & Lt; / código de & gt; pre>
Y luego hay que volver a los valores originales del vector de coeficientes.
& lt; code class = & quot; MATLAB & quot; & gt; a0 (1) = a0 (1) * norm_speed_temp / norm_4_temp; a0 (2) = a0 (2) * norm_speed_temp / norm_int_temp; a0 (3) = a0 (3) * norm_speed_temp / norm_int_power; a0 (4) = a0 (4) * norm_speed_temp / norm_constant; & Lt; / código de & gt; pre>
Como resultado, el siguiente valor a0 = [- 1.073D-12-,0029096, 0,0004617, 2,0969723], que está cerca el resultado de nuestros colegas extranjeros , a pesar de que utilizan un tubo de calefacción.
Ahora ya está listo para comprobar los resultados obtenidos en el modelo. Para ello utilizamos el paquete de simulación virtual de Xcos Scilab. Puesto que tenemos una ecuación diferencial que describe el proceso térmico en el reactor, y todos los coeficientes a, entonces recoger el siguiente esquema.
Bloquear «Desde Workspace» servir a la capacidad de datos experimentales previamente para esta estructura de bloque se crea V. Fijamos la frecuencia de muestreo y la hora de inicio de la simulación en el bloque «reloj». La longitud de la estructura de datos de salida se establece en la entrada. El tiempo de simulación final debe ser igual al tiempo del experimento. Modelización de riego en el programa y comparar los gráficos de la experimentación y simulación.
& lt; code class = & quot; MATLAB & quot; & gt; V.time = xx; V.values = int_power; importXcosDiagram (& quot; D: \ PhD \ Term_model.zcos & quot;); xcos_simulate (scs_m, 4); plot (tiempo, temperatura); parcela (A.time, A.values, & quot; r - & quot;); & Lt; / código de & gt; pre>
Éstos son los mismos, pero para la perturbación armónica con diferentes frecuencias.
Muchas gracias supervisor de Arastas por su valiosa asistencia y participación en la preparación del material. Gracias Zavarina Eugene para acceder a la aplicación de instalación y software de todos los experimentos.
Fuente: habrahabr.ru/post/218297/