1574
快速热过程的识别
最近,我才得以完成的工作在约费研究所一个非常有趣的项目。越飞和获得足够的实验数据与您分享。
物理学圣彼得堡约费研究院。约费从事生长氮化镓半导体结构,其具有在过渡电荷载体和一个大的热导率的良好的性能的速度。这种结构的生长过程发生在1000℃(1273 K)和常压下的温度。一切都发生在位于密封区域中的特别分庭。当越来越多的结构,并用氮气充满反应器的整个体积,密封带区域。在衬底保持器的结构的生长被旋转以每秒一次的速率。这种操作涉及在快速热处理过程中,温度的变化率范围从几到几百度每秒。

我的任务是,以控制所述石墨衬底支架的通过感应加热装置的温度。
技术特点如下。对于温度测量,激光温度计,在石墨的中心去除的数据。信息检索的频率为每秒10次,测量步骤1度。发射功率石墨的值依赖成正比的功率电感器。在发电机控制电感器具有数字输出,它携带的电压,电流和功率。
一开始,有必要调整温度控制成长的过程中一直没有强烈的波动。面对这个任务的速度不够快,但我们的决定只有在高温下给高品质的成果。用于改变系数所需的其他进程。
由于这项工作融入我的博士的主题,想写基于热过程模型的分析,一些聪明的控制算法。开始熟悉法律史蒂芬 - 玻尔兹曼时,功率黑体辐射是成正比的表面积和第四度的温度。鉴于对流可以写一个公式,温度去除
热过程
其中T - 温度,P - 功率,锝 - 周围物体,这是由辐射的石墨,钽加热的温度 - 近的地点信息的检索它执行对流气体的温度,B,A1,A2 - 的系数来识别。为了简化替换等式,这可以被认为是在稳定过程恒定的所有组成部分,并考虑下面的等式
我们现在有可从该推的数据的进一步分析的模型。在实验中,将信号馈送到弯曲。
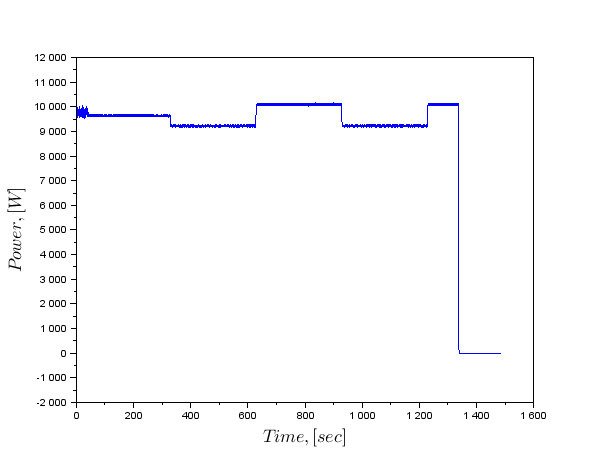
如果我们获得温度的变化率的估计值,将有可能使用公知的温度和所述电感器的功率控制的回归模型,并计算公式中的系数。
我很早就一直在使用 Scilab的这一次决定不更改sebe.Dlya这个任务我选择了推导傅立叶级数的形式。但开始使用真实的数据,它是必要的内插的测量,以获得一个均匀的时间轴。
<预>&LT;代码类= QUOT; MATLAB&QUOT;&GT; XX = linspace(0,圆(时间($)),圆(时间($))* FS + 1)'; //新的时间坐标轴'D = splin(时间,温度,和QUOT;单调&QUOT;); [Int_temp,int_temp_diff] =插值(XX,时间,温度,D);和中尉; /码&GT; PRE>
值得一提的是,该变量«int_temp_diff»将包含数据速率,但它们看起来非常不偏袒。
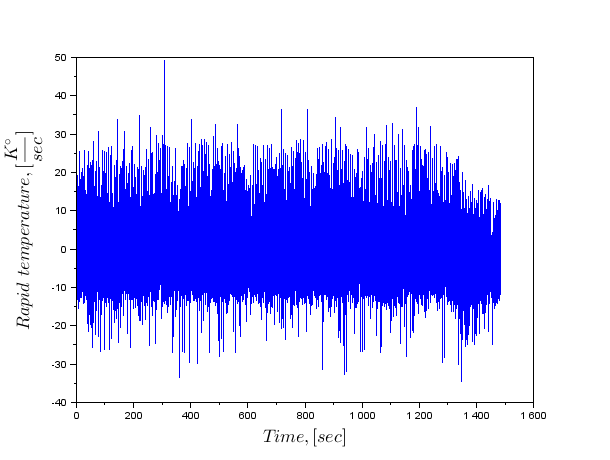
因此,获得与傅里叶级数的形式数据。我们需要建立一个在年底没有休息,挂图温度数据的附加尾部的数据。
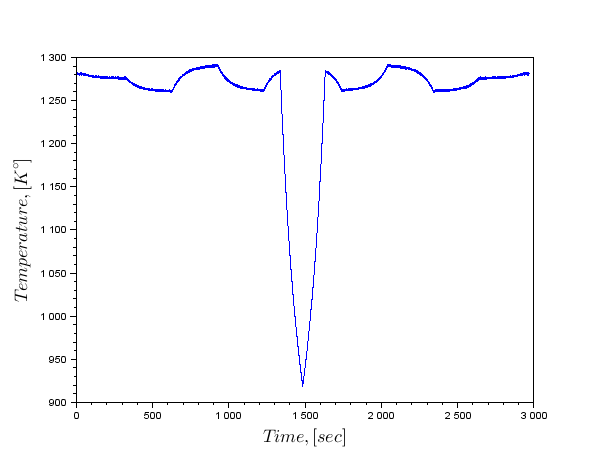
然后问频率轴做离散傅里叶变换。

<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT; FS = 10;在= //采样频率[int_temp; int_temp($: - 1:1)]; N =长度(英寸);频率= [0:(N-1)] / N * fs的;频率(N / 2 + 1:$)=频率(N / 2 + 1:$)-fs;频率=频率“; SP = FFT(上); //快速傅立叶变换&LT; /码&GT; PRE>
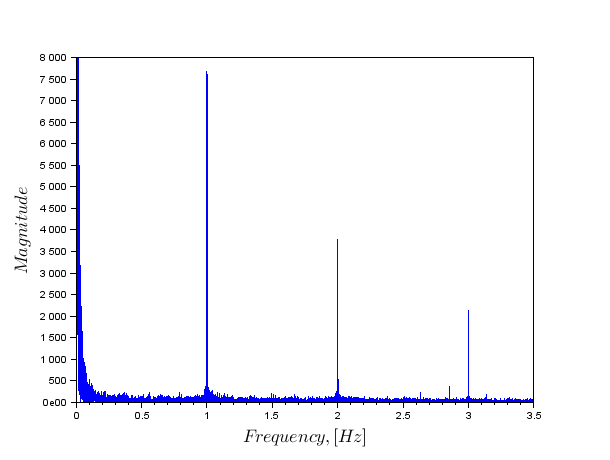
在1赫兹的频率,可以看到清晰的峰是由于这样的事实,即在衬底保持器被旋转与该频率。其他采样频率由于该石墨不均匀加热,在旋转的温度可以增加和减少几倍的事实。
要利用傅立叶变换衍生,只需乘以。在此之后,执行逆傅立叶变换。
<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT;欧米茄=(2 * PI%*%I *频率); TMP = SP *欧米茄。出实=(FFT(TMP,1)); speed_temp = OUT(1:N / 2);和中尉; /码&GT; PRE>
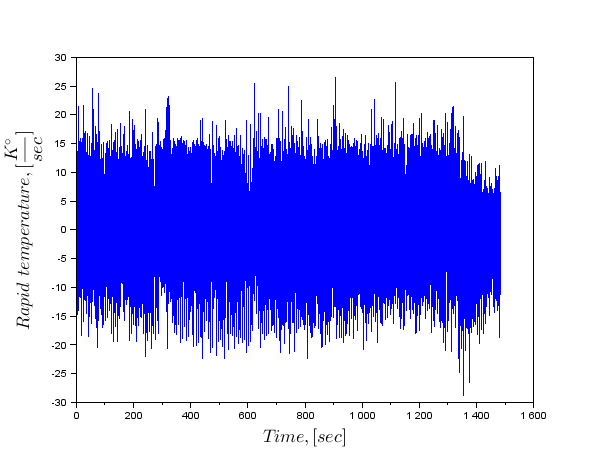
这当然比通过三次样条由推导返回更好一点,但这个问题不合格结果的鉴定。不得不求助于信号滤波。
在我的朋友汝拉,其中涉及船舶控制系统的设置的意见,因此决定使用一个窗口布莱克曼 - 哈里斯来削减不必要的频率。因为在生长曲线图的过程转动以每秒1次的频率,具有高于该频率的所有振荡我们不感兴趣。因此,有必要切下所有的波动上述1 [Hz]的方法:
<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT; CF = 1; //截止频率k = ROUND(CF * N / FS); L = 2 * K + 1; A0 = 0.35875; A1 = 0.48829; A2 = 0.14128; A3 = 0.01168;对于j = 0:L-1瓦特第(j + 1)= A0 - A1 * COS(2 *%PI *焦耳/(L-1))+ A2 * COS(4 *%PI *焦耳/(L- 1)) - A3 * COS(6 *%PI *焦耳/(L-1));最终H =零(频率);对于j = 1:1:K + 1小时(J)= W(K + j)条;端H([$: - 1:$ - k]的)= H([1:1:K + 1]);欧米茄=(2 * PI%*%I *频率);欧米茄=欧米茄* H; TMP = SP *欧米茄。出实=(FFT(TMP,1)); speed_temp = OUT(1:N / 2);和中尉; /码&GT; PRE>
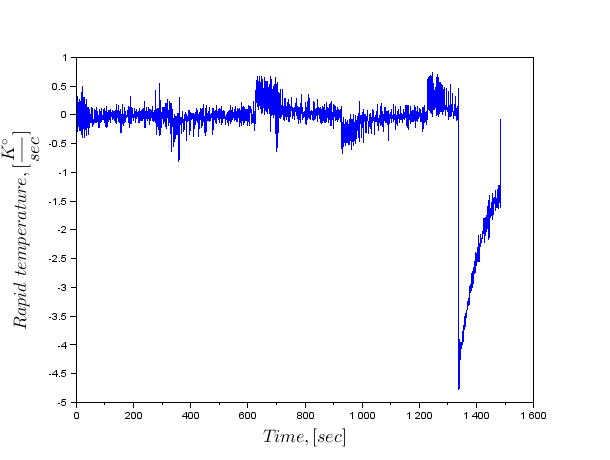
好多了。与此开始到回归系数的计算。
为了获得良好的数据,你首先必须标准化矢量数据。对于方程必须指定向量填充单元在自由常数。
<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT;常数(1:长度(int_power))= 1; norm_4_temp =规范(int_temp ^ 4); norm_int_temp =规范(int_temp); norm_int_power =规范(int_power); norm_speed_temp =规范(speed_temp); norm_constant =标准(不变);和中尉; /码&GT; PRE>
现在,您可以找到常量的值。含有三个变量和常量的值的矩阵的分量。在此由它的长度将每个数据载体。为系数必须乘以伪逆矩阵为温度变化的归一化矢量数据速率。
<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT; LSM = [int_temp ^ 4 / norm_4_temp,int_temp / norm_int_temp,int_power / norm_int_power,恒/ norm_constant]; A0 = PINV(LSM)* speed_temp / norm_speed_temp;和中尉; /码&GT; PRE>
然后,你必须回到系数向量的初始值。
<预>&LT;代码类= QUOT; MATLAB&QUOT;&GT; A0(1)= A0(1)* norm_speed_temp / norm_4_temp; A0(2)= A0(2)* norm_speed_temp / norm_int_temp; A0(3)= A0(3)* norm_speed_temp / norm_int_power; A0(4)= A0(4)* norm_speed_temp / norm_constant;和中尉; /码&GT; PRE>
其结果,下面的值A0 = [ - 1.073D-12 - 0.0029096,0.0004617,2.0969723],这是接近的我们的外国同事的,但他们用管加热。
现在,您可以检查模型得到的结果。为此,我们使用虚拟仿真包Xcos的Scilab。因为我们有一个微分方程描述的热过程中的反应器中,所有系数它,然后收集以下方案。
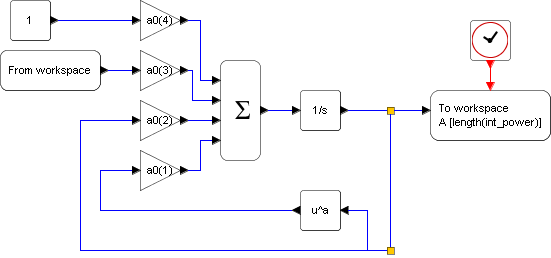
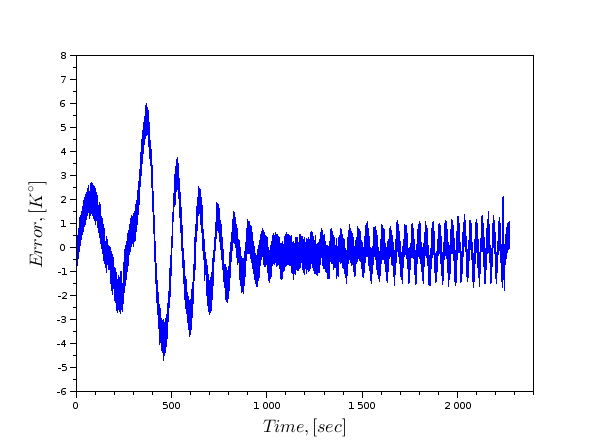
块«从工作区»服务于实验数据容量先前对于该块结构被创建五我们设定的采样频率和在块«时钟»模拟的开始时间。输出数据结构的长度被设定为输入。最后模拟时间应等于实验的时间。建模运行中的程序和比较实验和模拟的图形。
<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT; V.time = XX; V.values = int_power; importXcosDiagram(&QUOT; D:\博士\ Term_model.zcos&QUOT;); xcos_simulate(scs_m,4);图(时间,温度);图(A.time,A.values,与QUOT; R - &QUOT;);和中尉; /码&GT; PRE>
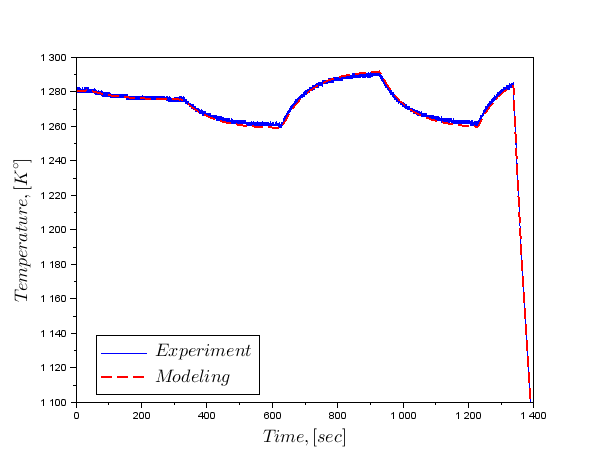
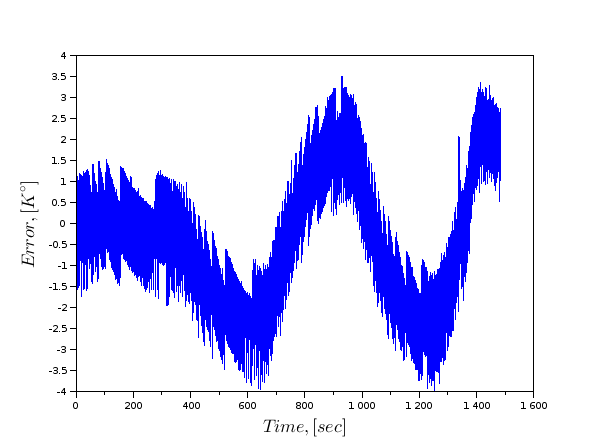
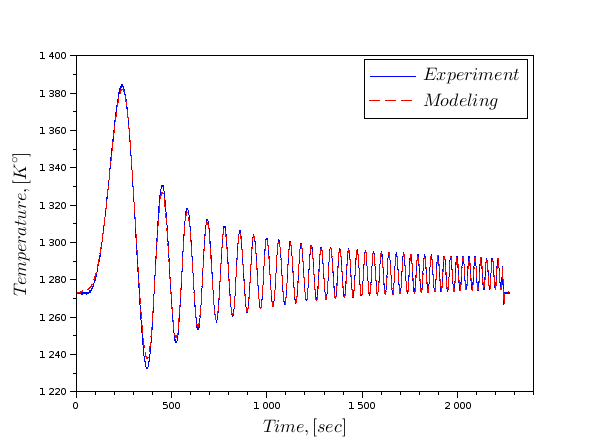
这里是相同的,但对于谐波干扰具有不同的频率。
非常感谢主管 Arastas 在材料的制备的宝贵援助和参与。感谢Zavarina尤金访问安装和软件实现所有的实验。
来源: habrahabr.ru/post/218297/
物理学圣彼得堡约费研究院。约费从事生长氮化镓半导体结构,其具有在过渡电荷载体和一个大的热导率的良好的性能的速度。这种结构的生长过程发生在1000℃(1273 K)和常压下的温度。一切都发生在位于密封区域中的特别分庭。当越来越多的结构,并用氮气充满反应器的整个体积,密封带区域。在衬底保持器的结构的生长被旋转以每秒一次的速率。这种操作涉及在快速热处理过程中,温度的变化率范围从几到几百度每秒。

我的任务是,以控制所述石墨衬底支架的通过感应加热装置的温度。
技术特点如下。对于温度测量,激光温度计,在石墨的中心去除的数据。信息检索的频率为每秒10次,测量步骤1度。发射功率石墨的值依赖成正比的功率电感器。在发电机控制电感器具有数字输出,它携带的电压,电流和功率。
一开始,有必要调整温度控制成长的过程中一直没有强烈的波动。面对这个任务的速度不够快,但我们的决定只有在高温下给高品质的成果。用于改变系数所需的其他进程。
由于这项工作融入我的博士的主题,想写基于热过程模型的分析,一些聪明的控制算法。开始熟悉法律史蒂芬 - 玻尔兹曼时,功率黑体辐射是成正比的表面积和第四度的温度。鉴于对流可以写一个公式,温度去除
热过程
其中T - 温度,P - 功率,锝 - 周围物体,这是由辐射的石墨,钽加热的温度 - 近的地点信息的检索它执行对流气体的温度,B,A1,A2 - 的系数来识别。为了简化替换等式,这可以被认为是在稳定过程恒定的所有组成部分,并考虑下面的等式
我们现在有可从该推的数据的进一步分析的模型。在实验中,将信号馈送到弯曲。

如果我们获得温度的变化率的估计值,将有可能使用公知的温度和所述电感器的功率控制的回归模型,并计算公式中的系数。
我很早就一直在使用 Scilab的这一次决定不更改sebe.Dlya这个任务我选择了推导傅立叶级数的形式。但开始使用真实的数据,它是必要的内插的测量,以获得一个均匀的时间轴。
<预>&LT;代码类= QUOT; MATLAB&QUOT;&GT; XX = linspace(0,圆(时间($)),圆(时间($))* FS + 1)'; //新的时间坐标轴'D = splin(时间,温度,和QUOT;单调&QUOT;); [Int_temp,int_temp_diff] =插值(XX,时间,温度,D);和中尉; /码&GT; PRE>
值得一提的是,该变量«int_temp_diff»将包含数据速率,但它们看起来非常不偏袒。

因此,获得与傅里叶级数的形式数据。我们需要建立一个在年底没有休息,挂图温度数据的附加尾部的数据。

然后问频率轴做离散傅里叶变换。

<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT; FS = 10;在= //采样频率[int_temp; int_temp($: - 1:1)]; N =长度(英寸);频率= [0:(N-1)] / N * fs的;频率(N / 2 + 1:$)=频率(N / 2 + 1:$)-fs;频率=频率“; SP = FFT(上); //快速傅立叶变换&LT; /码&GT; PRE>

在1赫兹的频率,可以看到清晰的峰是由于这样的事实,即在衬底保持器被旋转与该频率。其他采样频率由于该石墨不均匀加热,在旋转的温度可以增加和减少几倍的事实。
要利用傅立叶变换衍生,只需乘以。在此之后,执行逆傅立叶变换。
<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT;欧米茄=(2 * PI%*%I *频率); TMP = SP *欧米茄。出实=(FFT(TMP,1)); speed_temp = OUT(1:N / 2);和中尉; /码&GT; PRE>

这当然比通过三次样条由推导返回更好一点,但这个问题不合格结果的鉴定。不得不求助于信号滤波。
在我的朋友汝拉,其中涉及船舶控制系统的设置的意见,因此决定使用一个窗口布莱克曼 - 哈里斯来削减不必要的频率。因为在生长曲线图的过程转动以每秒1次的频率,具有高于该频率的所有振荡我们不感兴趣。因此,有必要切下所有的波动上述1 [Hz]的方法:
<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT; CF = 1; //截止频率k = ROUND(CF * N / FS); L = 2 * K + 1; A0 = 0.35875; A1 = 0.48829; A2 = 0.14128; A3 = 0.01168;对于j = 0:L-1瓦特第(j + 1)= A0 - A1 * COS(2 *%PI *焦耳/(L-1))+ A2 * COS(4 *%PI *焦耳/(L- 1)) - A3 * COS(6 *%PI *焦耳/(L-1));最终H =零(频率);对于j = 1:1:K + 1小时(J)= W(K + j)条;端H([$: - 1:$ - k]的)= H([1:1:K + 1]);欧米茄=(2 * PI%*%I *频率);欧米茄=欧米茄* H; TMP = SP *欧米茄。出实=(FFT(TMP,1)); speed_temp = OUT(1:N / 2);和中尉; /码&GT; PRE>

好多了。与此开始到回归系数的计算。
为了获得良好的数据,你首先必须标准化矢量数据。对于方程必须指定向量填充单元在自由常数。
<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT;常数(1:长度(int_power))= 1; norm_4_temp =规范(int_temp ^ 4); norm_int_temp =规范(int_temp); norm_int_power =规范(int_power); norm_speed_temp =规范(speed_temp); norm_constant =标准(不变);和中尉; /码&GT; PRE>
现在,您可以找到常量的值。含有三个变量和常量的值的矩阵的分量。在此由它的长度将每个数据载体。为系数必须乘以伪逆矩阵为温度变化的归一化矢量数据速率。
<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT; LSM = [int_temp ^ 4 / norm_4_temp,int_temp / norm_int_temp,int_power / norm_int_power,恒/ norm_constant]; A0 = PINV(LSM)* speed_temp / norm_speed_temp;和中尉; /码&GT; PRE>
然后,你必须回到系数向量的初始值。
<预>&LT;代码类= QUOT; MATLAB&QUOT;&GT; A0(1)= A0(1)* norm_speed_temp / norm_4_temp; A0(2)= A0(2)* norm_speed_temp / norm_int_temp; A0(3)= A0(3)* norm_speed_temp / norm_int_power; A0(4)= A0(4)* norm_speed_temp / norm_constant;和中尉; /码&GT; PRE>
其结果,下面的值A0 = [ - 1.073D-12 - 0.0029096,0.0004617,2.0969723],这是接近的我们的外国同事的,但他们用管加热。
现在,您可以检查模型得到的结果。为此,我们使用虚拟仿真包Xcos的Scilab。因为我们有一个微分方程描述的热过程中的反应器中,所有系数它,然后收集以下方案。

块«从工作区»服务于实验数据容量先前对于该块结构被创建五我们设定的采样频率和在块«时钟»模拟的开始时间。输出数据结构的长度被设定为输入。最后模拟时间应等于实验的时间。建模运行中的程序和比较实验和模拟的图形。
<前>&LT;代码级=&QUOT; MATLAB&QUOT;&GT; V.time = XX; V.values = int_power; importXcosDiagram(&QUOT; D:\博士\ Term_model.zcos&QUOT;); xcos_simulate(scs_m,4);图(时间,温度);图(A.time,A.values,与QUOT; R - &QUOT;);和中尉; /码&GT; PRE>


这里是相同的,但对于谐波干扰具有不同的频率。


非常感谢主管 Arastas 在材料的制备的宝贵援助和参与。感谢Zavarina尤金访问安装和软件实现所有的实验。
来源: habrahabr.ru/post/218297/