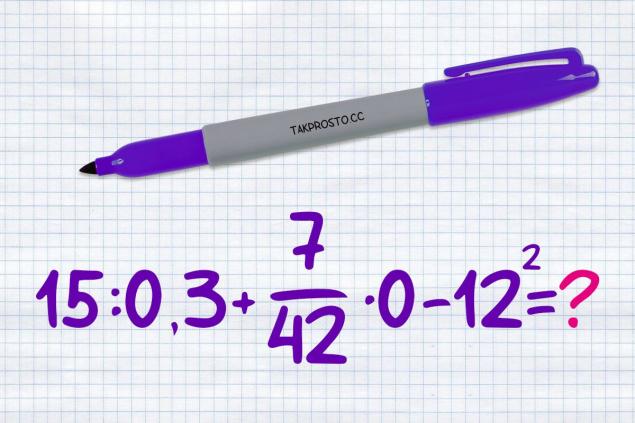Compruebe si puede resolver el ejemplo de un niño sin una calculadora

¿Cómo aprendes a contar en tu mente? ¿Y por qué haces eso cuando casi siempre tienes una calculadora a mano? El hecho es que el contar verbal desarrolla el pensamiento. Además, cuando cuenta sin los medios a mano, siente un nivel muy diferente de control de la realidad.



Usted sabe con anticipación cuánto cambio se le dará en la tienda y si vale la pena meter a todos en el ascensor si su capacidad de carga es de 400 kg. El uso de una calculadora, por el contrario, nos enseña a confiar ciegamente en una técnica cuyo principio de operación ni siquiera entendemos. Esto debilita nuestra atención y nos desalienta de pensar para nosotros mismos.

Antes compartimos secretos matemáticos y trucos que ayudan a multiplicarse y dividir en la mente. Hoy te ofrecemos algunos ejemplos de prueba. ¿Recuerdas bien el currículo escolar? ¡Entonces intenta completar nuestras tareas en 15 segundos!

1. Cuenta sin la calculadora.
   Añadir 1000 y 40. Añadir otros 1.000. Ahora 30. 1.000 de nuevo. A continuación, añadir 20. 1.000 de nuevo. 10 más. Resolver este problema, trate de hacer todos los cálculos rápidamente y en su mente. No escriba ni use una calculadora. Estoy seguro de que el resultado te sorprenderá.
   
   
   
2. ¿Cuánto es?
   En la escuela, hicimos clic en ejemplos como nueces. Pero con el tiempo, se ha olvidado mucho. Por ejemplo, ¿alguien recuerda cómo dividirse en fracciones?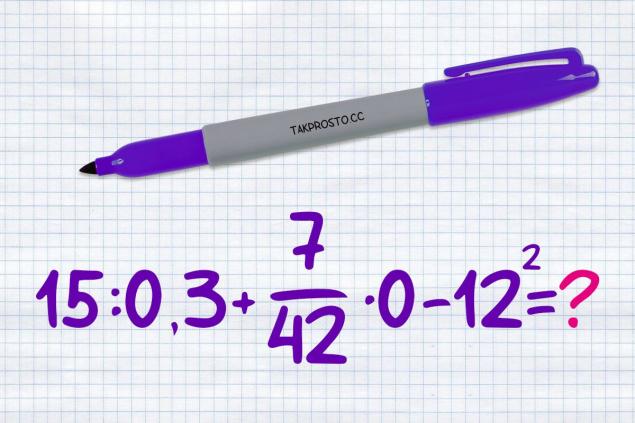
   
   
   
3. Ejemplo complicado y 15 segundos de tiempo
   fracciones sólidas, e incluso elevadas en grado ... El ejemplo parece demasiado complicado. Pero como dijo el profesor de matemáticas, cualquier expresión puede ser simplificada.
   
   
   
4. Ten cuidado.
   ¡Wow, negativo! Me rindo. Creo que estaba enfermo cuando pasamos por esto.
   
   
   

Respuestas.

1. Parecería simple. Pero los comentarios sugieren lo contrario. Por alguna razón, la mayoría de los usuarios de Internet tienen 5.000. Y hay quienes contaron 5100, 4910 e incluso 2060. Al mismo tiempo, los abogados gravitan a la última variante de la respuesta: dicen, si no hay palabra "add" antes del número, entonces no es necesario considerarlo.
   
   Peels
   
   En realidad, La respuesta correcta es 4100.1000 + 40 = 1040; 1040 + 1000 = 2040; 2040 + 30 = 2070; 2070 + 1000 = 3070; 3070 + 1000 = 4090; 4090 + 10 = 4100.. Pero después de 4090, cuando la gente añade 10, muchos obtienen 5.000. Parece que en algunos casos tratamos psicológicamente de ajustar la respuesta a un número más redondo. En otros, en lugar de 90, recordamos 900. En resumen, es una tarea consciente que tan a menudo nos falta.
   
   
2. Dividir un número por una fracción es como multiplicarlo por la misma fracción, habiendo cambiado previamente el numerador y los lugares denominadores. Cualquier número multiplicado por 0 sigue siendo 0. Entonces nuestro ejemplo obtiene una forma más comprensible: 15 x 10: 3 - 144 = 50 - 144 = -94.
3. Ya hemos arreglado las fracciones un poco. Multiplicación por fracción en el numerador del cual la unidad es reemplazada por división por el denominador de la misma fracción. Dividir por un segundo es lo mismo que multiplicarse por dos. El resultado es: 32:16 + 61 x 2 = 124
4. Parece que tendremos que deshacernos del orden olvidado de las acciones matemáticas. Todos lo enseñamos en la escuela primaria: corchetes, grado, multiplicación, división, adición, resta. Aplicamos la regla y primero ponemos una quinta parte en un estado negativo. Para hacer esto, sólo tiene que cambiar el numerador y el denominador y erigir el número resultante en un cuadrado. Eso hace 25. Luego dividimos, luego multiplicamos y agregamos. 25:25 + 12:2 x 3 = 1 + 6 x 3 = 1 + 18 = 19. Respuesta correcta: 19.
   
   

A menudo resentimos el hecho de que la escuela no enseña en absoluto lo que es útil en la vida real. Sí, nuestro sistema educativo está demasiado obsoleto y sigue obsoleto todos los días. Pero una persona bien educada nunca se perderá en una situación difícil y será capaz de encontrar una salida de ella.