540
Bad children grow up to be good parents: 5 scientific paradoxes
Everyone likes a beautiful horse, but no one else wanted to be. With each generation of children is getting worse, and parents better; hence, more poor children grow up to be better parents. The list of paradoxes of the infinite — we will tell only about most interesting of them.

The paradox of the birthdays
This statement says that in a group of 23 or more people the probability that at least two of them will match the birthday (day and month) exceeds 50%. For 60 or more people, this probability exceeds 99%, but 100% of it, according to the so-called Dirichlet principle, will reach only when in a group will be at least 367 people.
This statement may seem obvious, since the probability of coincidence of birthdays of the two people any day of the year (1/365 = 0.27%, respectively), multiplied by the number of people in the group of 23 participants, gives only 23/365 = 6.3 percent. However, such reasoning is incorrect, as the number of possible pairs (253) far exceeds the number of people in the group. Therefore, the statement is not to be considered strictly scientific paradox: logical contradictions in it, and the paradox lies only in the difference between the intuitive perception of such circumstances, the person and the results of mathematical calculations.
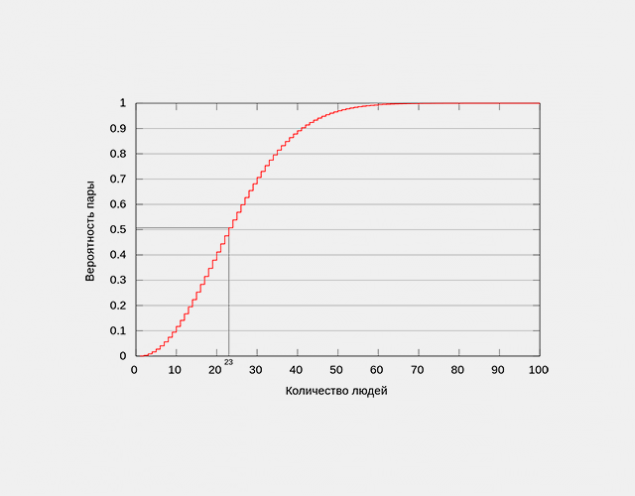
Graph showing the probability of coincidence of birthdays of at least two people from a specified number of people
The paradox of the liarIs the statement "what I am saying now is false". The statement contradicts one of the fundamental principles of classical mathematics, the law of the excluded middle (is that from the two statements "A" and "not," one is necessarily false and the second true, that is, both statements can't both be false — NS).
Assuming that this statement is true, then based on its content, it is also true that it is false. But if it is false then what it says is wrong. Therefore, it is wrong and that this statement is a lie. So the statement is true. In the end we return to the beginning of the reasoning.
The paradox of the crocodileIn its structure, the fallacy is reminiscent of the paradox of the liar. The author of the paradox considered Greek orator Corax. The wording of the paradox is as follows. The crocodile snatched the Egyptian women standing by the river, her child. Her request to return the child crocodile said, "I'll give you a chance to return it, but you have to guess I will give it to you or not. Answer correctly I will give up baby, no — I'll leave myself." The mother replied, "You don't give me the baby." "Do not give up,' replied the crocodile, because you either told the truth or lied. If what I will not give up the child, however, I'm not giving it, otherwise it is said not to be true. If this thing is not true, then you have not guessed, I will not give up the child by agreement". The mother replied, "But if I told the truth, you'll give me the child, as we agreed. If I didn't guess that you don't give the child, then I need to give it away, otherwise what I said will not be true". Who is right — the mother or the crocodile?
The promise of a crocodile is self-contradictory, and therefore impossible based on the laws of logic.
The paradox of Curry, "If this is true, then mermaids exist", reads this statement. Let's try to disprove it. We denote the statement "A". If "A" is true, then mermaids exist. But we don't know whether it is true "A". If "A" was true, it would mean the existence of mermaids. But it says "A" then statement "A" — right. Consequently, mermaids exist.
The paradox Curry — use assertion references to itself, which is unacceptable.
The theory of the greater foolBut this paradox we have to face constantly. The theory of the greater fool might be called the Theory of UM. She claims that you can make money in any securities, regardless of their value, first purchasing and then selling at a profit, because there is always someone more stupid (the greater fool), who also expects to quickly resell the asset at a profit. On this principle are speculative bubbles, which must burst, bringing down price to the mass market.published
P. S. And remember, just changing your mind — together we change the world! ©
Source: www.factroom.ru/science/5-scientific-paradoxes

The paradox of the birthdays
This statement says that in a group of 23 or more people the probability that at least two of them will match the birthday (day and month) exceeds 50%. For 60 or more people, this probability exceeds 99%, but 100% of it, according to the so-called Dirichlet principle, will reach only when in a group will be at least 367 people.
This statement may seem obvious, since the probability of coincidence of birthdays of the two people any day of the year (1/365 = 0.27%, respectively), multiplied by the number of people in the group of 23 participants, gives only 23/365 = 6.3 percent. However, such reasoning is incorrect, as the number of possible pairs (253) far exceeds the number of people in the group. Therefore, the statement is not to be considered strictly scientific paradox: logical contradictions in it, and the paradox lies only in the difference between the intuitive perception of such circumstances, the person and the results of mathematical calculations.

Graph showing the probability of coincidence of birthdays of at least two people from a specified number of people
The paradox of the liarIs the statement "what I am saying now is false". The statement contradicts one of the fundamental principles of classical mathematics, the law of the excluded middle (is that from the two statements "A" and "not," one is necessarily false and the second true, that is, both statements can't both be false — NS).
Assuming that this statement is true, then based on its content, it is also true that it is false. But if it is false then what it says is wrong. Therefore, it is wrong and that this statement is a lie. So the statement is true. In the end we return to the beginning of the reasoning.
The paradox of the crocodileIn its structure, the fallacy is reminiscent of the paradox of the liar. The author of the paradox considered Greek orator Corax. The wording of the paradox is as follows. The crocodile snatched the Egyptian women standing by the river, her child. Her request to return the child crocodile said, "I'll give you a chance to return it, but you have to guess I will give it to you or not. Answer correctly I will give up baby, no — I'll leave myself." The mother replied, "You don't give me the baby." "Do not give up,' replied the crocodile, because you either told the truth or lied. If what I will not give up the child, however, I'm not giving it, otherwise it is said not to be true. If this thing is not true, then you have not guessed, I will not give up the child by agreement". The mother replied, "But if I told the truth, you'll give me the child, as we agreed. If I didn't guess that you don't give the child, then I need to give it away, otherwise what I said will not be true". Who is right — the mother or the crocodile?
The promise of a crocodile is self-contradictory, and therefore impossible based on the laws of logic.
The paradox of Curry, "If this is true, then mermaids exist", reads this statement. Let's try to disprove it. We denote the statement "A". If "A" is true, then mermaids exist. But we don't know whether it is true "A". If "A" was true, it would mean the existence of mermaids. But it says "A" then statement "A" — right. Consequently, mermaids exist.
The paradox Curry — use assertion references to itself, which is unacceptable.
The theory of the greater foolBut this paradox we have to face constantly. The theory of the greater fool might be called the Theory of UM. She claims that you can make money in any securities, regardless of their value, first purchasing and then selling at a profit, because there is always someone more stupid (the greater fool), who also expects to quickly resell the asset at a profit. On this principle are speculative bubbles, which must burst, bringing down price to the mass market.published
P. S. And remember, just changing your mind — together we change the world! ©
Source: www.factroom.ru/science/5-scientific-paradoxes