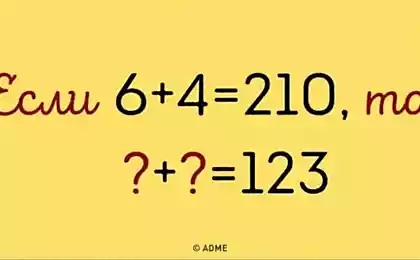The famous logic puzzle on green-eyed

Imagine an island where a mad dictator holds in custody 100 people, and they are all excellent mathematics. Escape is impossible, but there is a strange rule. At night, any prisoner in custody may request release. If the prisoner green eyes, he would be released. If not, throw it into the mouth of a volcano.

< In fact, of all 100 inmates green eyes
Yet every morning they are seen on the roll. Everyone knows that no one even dares to ask for freedom, without being absolutely sure of success. Unable to withstand the pressure of human rights organizations, the dictator reluctantly allows you to visit the island and talk to the prisoners. But he puts a condition: you make only one application, and you do not inform prisoners of the new information. ? How to help prisoners and not to incur the wrath of the dictator

After much thought, you say a crowd of prisoners:. "At least one of you green eyes» The dictator executed distrust, but He calms himself: such a statement does not change anything. You're leaving, but life on the island as if it goes on. But one morning, 100 days after your visit, the island is empty - all the prisoners demanded the release last night. < How did you manage to fool the dictator?



OTVETOTVET

It is important to understand that the number of prisoners does not matter. Let's simplify the problem and pretend that there are only two - Adria and Bill. Each of them sees prisoner with green eyes, but he knows that this may be the only green-eyed.



The first night, both are waiting. The next morning they see a friend is still here, and it gives them a hint: Adria realize that if her eyes were green, the Bill would be released on the first night, he realized that he - the only green-eyed prisoner. Similarly, Bill talks about Adria. Now each of them understands: "Because the other is waiting, my eyes can only be green»

. And the next morning, both the prisoner leave the island. Now imagine that the three prisoners: Adria, Bill and Carl. Each of them sees two prisoners with green eyes, but not sure how many green-eyed see the others - two or only one. The first night the prisoners are waiting again, but until morning does not bring clarity.

Carl thinks: "If my eyes are not green, Adria and Bill just watch each other. So, the next night they are both gone. " However, on the third morning, Karl sees that they were, and understands that Adria and Bill watched him. Adria and Bill argue similarly, and on the third night, the three of them go

This is called inductive logic -. We are increasing the number of prisoners, and the arguments remain valid and do not depend on the number of prisoners The new information. It gives your statement not itself, but the fact that all the prisoners heard them simultaneously. Now all the prisoners not only know that at least one of them has green eyes, but also something that everyone follows all the green-eyed, and they all know it, and so on. D.

What every single prisoner does not know - whether it relates to the green-eyed, overseen by the others. < He finds it only when the pass so many nights, how many prisoners on the island




via www.youtube.com/watch?v=98TQv5IAtY8