590
The paradox of the stairs argues that reality is subjective
Thought experiment showing that each person has their own realnost
The paradox of stairs - a famous thought experiment demonstrates why you can place objects in spaces too small for them. Or why can not - depending on your point of view.
Although we may think that reality is objective, there are special cases, proving that it is not. Everyone has their own reality, and the reality of these times are incompatible. An example of how times and can serve as the paradox of the stairs.
Let's say you have a staircase and garage, and you can not put a ladder in the closed garage, because it is too long. To do this you have to open or to the front door, and then one end of the ladder will be visible in the driveway or the back door, in which case one end of the ladder would have in the backyard.
Once your friend Albert states that can put a ladder in the garage so that it fits entirely in it, but not for long - the fact that when objects are close to relativistic velocities, they become shorter. So you're sitting in your garage, and Albert, who is able, apparently, to run extremely fast, runs through his hands to the stairs, which at this time is shorter than usual. If you can close the two garage doors at the same time (and very fast), the staircase is really a little while will completely inside.
Have you thought about it and found a small problem: if Albert is running with a ladder under his arm, then his view is not moving staircase and garage. And, as the garage "rushes" past him, then it becomes even shorter than the staircase, which is thus in a garage again will not fit.
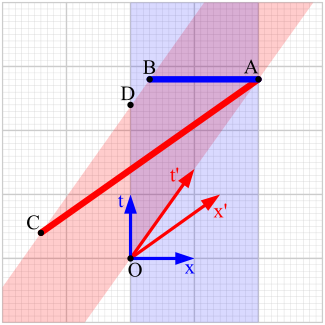
You decide to check. You are sitting in the garage, and as soon as Albert with stairs inside are quickly shut both doors at the same time - this will allow you to see what happens with the stairs. And, oddly enough, the staircase in the garage appropriate. But when you meet with Albert to discuss everything, he asks you why you do not shut both doors at the same time as he asked. You tell him that you did it, and he replied he argues that there is. "You were right, - says Albert - the garage is too short." And the only reason why the staircase does not put her in the door, that she has not been closed.
The back door is closed first, when he approached her, and stairs at this time is in motion. But when she almost put her in the back door closed, it opened again - then the ladder to proceed to the backyard. But in terms of Alberta, there was not a moment when there was a ladder in the garage, and both doors were closed at the same time.
Each of you received a different experience because of the length contraction and relativity of simultaneity. If you stand at an equal distance from the two lamps are connected to the same switch, and someone clicks the switch, you will see the bulb light up simultaneously. And the one who was standing next to a light bulb and away from each other, will see that the first light turns on his side, and the second - a little later.
Nothing can travel faster than light, even a molecule of the door - it means that you and Albert were right. The doors were opened and closed simultaneously, and the ladder fit and at the same time does not fit into the garage.
via factroom.ru

The paradox of stairs - a famous thought experiment demonstrates why you can place objects in spaces too small for them. Or why can not - depending on your point of view.
Although we may think that reality is objective, there are special cases, proving that it is not. Everyone has their own reality, and the reality of these times are incompatible. An example of how times and can serve as the paradox of the stairs.
Let's say you have a staircase and garage, and you can not put a ladder in the closed garage, because it is too long. To do this you have to open or to the front door, and then one end of the ladder will be visible in the driveway or the back door, in which case one end of the ladder would have in the backyard.
Once your friend Albert states that can put a ladder in the garage so that it fits entirely in it, but not for long - the fact that when objects are close to relativistic velocities, they become shorter. So you're sitting in your garage, and Albert, who is able, apparently, to run extremely fast, runs through his hands to the stairs, which at this time is shorter than usual. If you can close the two garage doors at the same time (and very fast), the staircase is really a little while will completely inside.
Have you thought about it and found a small problem: if Albert is running with a ladder under his arm, then his view is not moving staircase and garage. And, as the garage "rushes" past him, then it becomes even shorter than the staircase, which is thus in a garage again will not fit.

You decide to check. You are sitting in the garage, and as soon as Albert with stairs inside are quickly shut both doors at the same time - this will allow you to see what happens with the stairs. And, oddly enough, the staircase in the garage appropriate. But when you meet with Albert to discuss everything, he asks you why you do not shut both doors at the same time as he asked. You tell him that you did it, and he replied he argues that there is. "You were right, - says Albert - the garage is too short." And the only reason why the staircase does not put her in the door, that she has not been closed.
The back door is closed first, when he approached her, and stairs at this time is in motion. But when she almost put her in the back door closed, it opened again - then the ladder to proceed to the backyard. But in terms of Alberta, there was not a moment when there was a ladder in the garage, and both doors were closed at the same time.
Each of you received a different experience because of the length contraction and relativity of simultaneity. If you stand at an equal distance from the two lamps are connected to the same switch, and someone clicks the switch, you will see the bulb light up simultaneously. And the one who was standing next to a light bulb and away from each other, will see that the first light turns on his side, and the second - a little later.
Nothing can travel faster than light, even a molecule of the door - it means that you and Albert were right. The doors were opened and closed simultaneously, and the ladder fit and at the same time does not fit into the garage.
via factroom.ru