I know that a huge proportion of the audience of this resource - the specialists in various branches of science.
But I just know that visits him and a lot of people simply interested in the phenomena of nature (I carry myself to this type), that does not diminish their desire to know the universe as far as lack of imagination and patience!
Therefore, this article aims to entertain and perhaps encourage someone to a better understanding of the issue, as well as, quite simply, to bring a new vision and an idea already, seemingly familiar things.

So, about the stars h4> The fact that a person can see in the sky is not even remotely similar to what is actually happening there. What opens our eyes - this greatly reduced the past of our universe. So when it comes to the stars, the person is usually either there is an image of bright dots in the sky, or something very much resembling our sun, floating in the depths of space.
In fact, most of the stars are these "boring" gas, glowing balls. But there in the vastness of space and something incredible! Though it looks to us as small and dim dots in the sky.
I will not describe the scientific эволюцию Stars or диаграмму Hertzsprung-Russell . I want to show how diverse the notion of "star" and how this diversity nesootnosimo to the fact that in this term we are investing in childhood (and some, like me, and then to later).
Brown Dwarf h4> For example, here's a star - Gliese 229B. Brown dwarf.
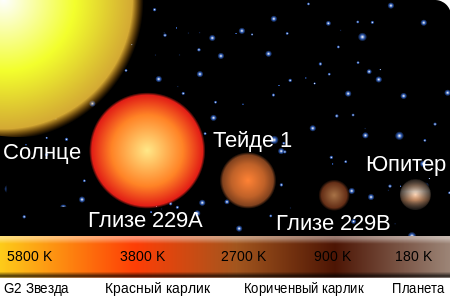
This is the exact opposite meaning of the word - "star" - shine, shine.
Jupiter is very similar to the star, and in fact, very little of it is different. Some species of brown dwarfs are called - hot Jupiters. But differences still there. Although the radius of the star and is comparable to the radius of the giant planets, they are mainly in the tens of times more massive and also emit in the infrared and X-rays.
Flying close to a star, we see her look like a kind of light-nightlight. No crown, bright glow, squinting eyes and the like. Imagine that you look at the sun through a welding mask. Reddish glowing planet of molten lava - that would look like the star to our eyes. And it is in the best case.
Ultra-cool brown dwarfs do not shine!
Being close, we probably would have seen a dark ball, overlapping the starry sky. And, if the distance from us to the star was the same as that from the Earth to the Sun, we generally are likely would not know that flies past the stars! Any planet usually covers at the center of its orbit the star, but the ultra-cool brown dwarf - and it is, therefore, no one to cover them.
It is also interesting that around brown dwarfs are also possible planetary systems! Scientists have found that often these, and so faint stars are surrounded by disks of dust, similar to the one from which our solar system formed.
It is sad that in heaven we nevoruzhennym eye can not see niodnogo brown dwarf. Even in the mountains, and with the best weather for observation.
Star system h4> We'll be lucky if our dwarf is part of the stars. Star system - two or more stars are bound together by gravitational forces.
Here, for example as seen telescopes dual system, part of which is the aforementioned Gliese 229B (small ball on the right).
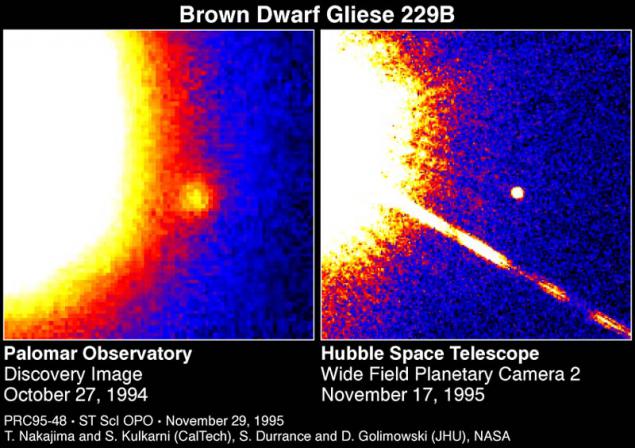
In this system, an ultra-cool brown dwarf would look very similar to some planet, a gas giant, rotating at a low orbit around the "normal" stars.
It turns out that the system of stars - not an uncommon phenomenon. And this is another amazing fact. Some of the stars that we see, in fact - huge star clusters, which we consider one bright a star because of the huge distances to them. And some - not so huge - so-called multiple stars. Let us examine each of the systems more.
Take any two stars in the sky that appear to us as close to each other. In fact, almost all of them are spaced from each other "deep" space. Almost all. There are exceptions.

For example, in the sky, clearly visible to our eyes the Pleiades. This star cluster, where the stars actually are "close" to one another. I wrote "close" in quotes - because the distance between them is calculated in light years. The radius of the cluster - about 12 light-years. For comparison, if our solar system is approximately in the center of the Pleiades, the most distant star cluster would be one and a half times the distance of our nearest Alpha Centauri.
When the weather is good and away from the cities can be distinguished 10-14 most prominent representatives of this cluster, but in fact they are there around 1000! Heaven on the planet within the Pleiades would look just magical! As part of the cluster mostly bright blue giants. They would decorate the sky beautiful blue-white lights, but, unfortunately, would not give life began, similar to ours because of the harmful radiation, literally permeates the entire region of the star system.
In clusters of stars usually do not have a clear center of mass. But there are systems such as the above-mentioned Gliese consisting of a multiple number of stars, which are to each other very closely, even by the standards of our solar system and orbit a common center of mass. They are called multiple systems of stars, or just multiple stars.
A good example - the system Mizar - Alcor in the constellation Ursa Major.
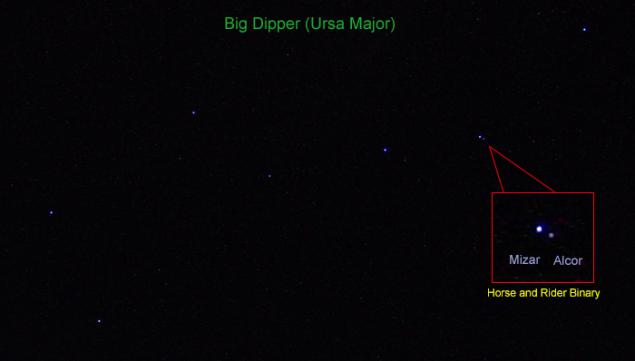
Look at the Big Dipper, even far from the city you'll notice that the second star of the bucket (Mizar) in the constellation is actually composed of two stars, the other - smaller - it Alcor. It is actually located physically close to a neighbor, and how we think - at a distance of a quarter of a light year. But even more interesting is that we see the two stars, and their six in this system!
And these multiple stars, as it turns out, is not uncommon. Very many of the stars that we see in the sky and considered as a single, in fact, double, triple, quadruple, quinary, and more! Why we do not notice? Because, as a rule, or "secondary" stars are too dim on the background of the "primary", which at times brighter, or the distance between them is so small that our eyes do not have enough resolution to a long distance divided into separate National Objects neighbors. < br />
In such systems, often the most interesting - is that neighbors can be different types of stars sama!
Sirius - the brightest star in the sky - in fact double.

The main star - a very common and unremarkable. In size it is only in 1, 7 times more than our sun. Only shines 22 times brighter and more white-blue light, in contrast to our star. Her companion - Sirius B - it is a white dwarf. Its radius is approximately equal to the radius of our Earth, and its mass is approximately equal to the mass of our Sun!
Superdense stars h4> The white dwarf - a small dim star in the past - the core of a red giant. The formation of these stars, without going into the details of the complex can be explained by the victory of gravity. Termination internal thermonuclear reactions in the red giant resets its shell and incredibly strong compression core. Matter of the star is so tightly in a small volume that 1 cubic centimeter of its material would weigh 10 tons in the world! Despite the seemingly dull appearance (flying around, we would see a white, glowing ball the size of a planetoid), the beauty of white dwarfs in their environment. Often, a massive explosion rips material from the surface of the red giant and with great speed carries it into the surrounding space. The resulting cloud, which we know as the nebula pleases our eyes all the colors of the chemical elements formed in the depths of the once pogibschey stars.

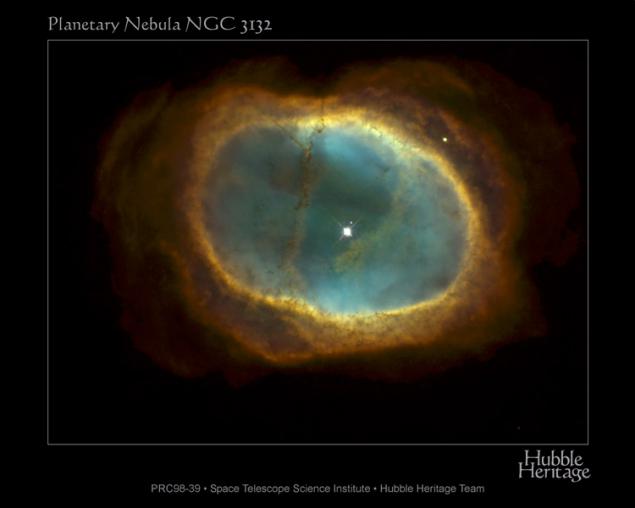
In the second picture nebula NGC 3132. Here, the main star is not a white dwarf (it - a little smaller and a little above), but it was he who caused the discharge of substances main star. Imagine what beauty we could watch from inside the nebula - orbit of this binary stars. Eye we would, nevertheless, to arm, to see something more than the usual sky with stars. So beautiful nebula looks only from afar. From a distance it seems dense cloud, but in reality, a substance highly dispersed, and near the most likely no different from our night sky. However, by placing the camera on a slow shutter speed on a hypothetical planet near the central star, we would see the fantastic beauty of the sky - a colorful nebula in the whole sky with its jumpers!
Remember the beautiful color photographs of the Milky Way. They are made with a slow shutter speed. Nothing like our eyes can not see.

With its small size, the white dwarf, because of the enormous weight has a significant gravitational influence on its surroundings. For example, a photo where, although most dwarf and is not visible, its influence can be clearly seen.

Here sphere on the right - a giant star, a substance which, mercilessly devoured located on the left a white dwarf. In this process, the material flows from one neighbor to another, twisting around the massive (although minuscule in comparison to victim) stars and gradually settles on its surface. Forms an accretion disk - a very beautiful phenomenon in terms of observation. Imagine Saturn's rings that glow like the sun. Only these rings far more twisted spiral and one end of the ring goes straight into the body of the star, forming elongated in the form of a giant wave on its surface! And in our sky, we can instead observe the usual point of light.
We now turn to the brother of a white dwarf - a neutron star.
When the red giant says goodbye to the life he has a chance to produce something more dense than white dwarf. If the star's mass exceeds the Chandrasekhar limit - from the nucleus giant formed neutron star. Its mass still comparable to the mass of the Sun, but the size does amazing - the radius of neutron stars only 10-20 kilometers! Because of the rapid decrease in size, like the skater spins up due to pulling hands to the body, these stars rotate at incredible speed! Many of neutron stars rotating at a speed of up to 1000 revolutions per second. This is about 10 times faster than the crankshaft car at maximum speed!
Interestingly, of the gravitational distortion, if we could see the heterogeneity of the surface of a neutron star, we would see more than half of the disc.

Neutron stars are also part of multiple systems and form the accretion disks.
Speaking of accretion disks worth, just to note the Cygnus X-1. While there, mneiyu scientists, is a black hole. In fact, this system is the first of the black hole candidates. The fact is that Cygnus X-1 strongly emits X-rays, and this is the first sign of the presence of a black hole and the accretion disk around it, formed at the expense of the donor - located next to a blue supergiant.
I do not advise fly up close to such systems, powerful radiation will kill every living thing on your spaceship for a long time before you get close enough at least to distinguish the light from the accretion disk giant.
Very nicely shows the accretion disk in the movie "Interstellar". But there is, unfortunately, was not the star-sacrifice.
Black holes - this is not quite the stars, and deserve, perhaps, a separate article, of which the Internet a huge number.
Planetary Systems h4> Finally, I would like to talk about the stars with planetary systems. The discovery of exoplanets is relatively recent, but the number has already found planets and candidates amazing! Just in the last year was opened a little less than a thousand exoplanets!
Remember, when you are 10-15 years ago, looked at the sky, how could you think that around the stars that you see billions of planets revolve? (According to an article in Wikipedia - в Milky Way about 100 billion planets. ).
How are planetary systems - we can say from personal experience - pretty boring if you're not near any of the planets.
But if the world just to form - the spectacle becomes much more interesting! Dust and gas gathering around a common center - luminous cloud, forming a pancake-shaped nebula illuminated from within. Star in the center still has no clear boundaries, and to see it does not allow a dense cloud around. Clots that may in the future become planets, smooth cast shadows, reaching the edges of the disc.
Likely to arm the eye is not even required - plostnost and lighting material will allow us to observe the birth of a new star system in all its glory.
Conclusion h4> It is amazing how much invested in the concept of Star, our ancestors, and how much it added in the last century! We can only wait, when humanity will be free to study celestial bodies approaching them directly, personally to confirm the theory, open at the tip of the pen. What more beautiful photos full of scientific articles? Just do what the world will be the stars of the future for us? ..
P.S.
I purposely did not spread here numerous paintings of artists will find all the stars in. Only photos and diagrams. Heard somewhere - what is the best graphics card in the world - this is our imagination!
Source: geektimes.ru/post/242578/