1118
Tic-tac-toe. Top version
One blogger tells us a new instruction to play tic-tac-toe, which he saw during a picnic.

298 One day I noticed a picnic mathematicians, crowding around the game of interest to which I expected the least: noughts and crosses.
You could themselves be noted that the game of noughts and crosses deadly boring. It is no place for a creative idea or sudden inspiration. Good players always play a draw.
But mathematicians at the picnic to play more sophisticated version of the game. In each of the cells on the square field, they drew a smaller field:

As the observation I noticed the basic rules:
Each turn is made in one of the small fields.

Reached in a small field location three identical pieces in a row wins this field.
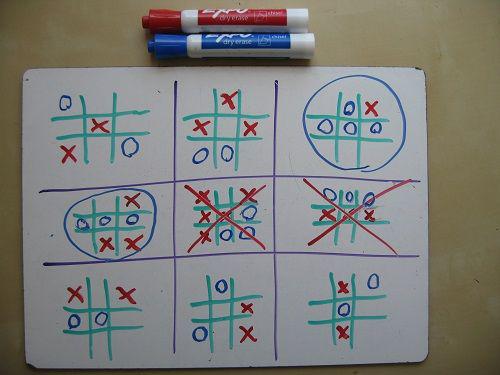
To win the game you need to win in three small fields in a row.
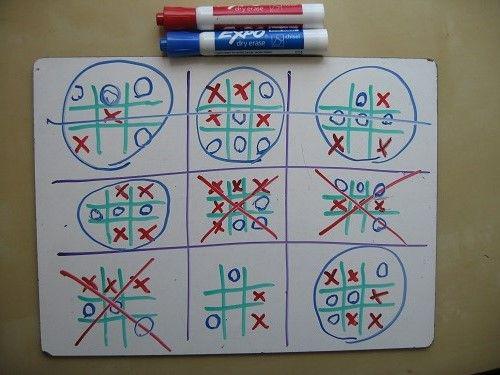
But to understand the most important rule, it took me a while:
The player does not select one of the nine small fields, where he wants to go. The choice is determined by the previous move of your opponent. A cell in a small field in which it went - it's a small field where you have to make a move. (And the cells into which you go, in turn, determines how small field will walk your opponent.) For example, if I go here ...

Your next move you will make here ...

This gives the game an element of strategy. You can not afford to focus on a small field. You have to take into account is where your turn to send your opponent, and where to send you the next move, and so on.
The result looks very unusual. Players can move randomly, easily flowing design in two or three identical pieces in a row. But this madness is the order - they think through their moves in advance, keeping in mind the possibility to send the opponent in the pristine property. It is generally much more interesting than the usual tic-tac.
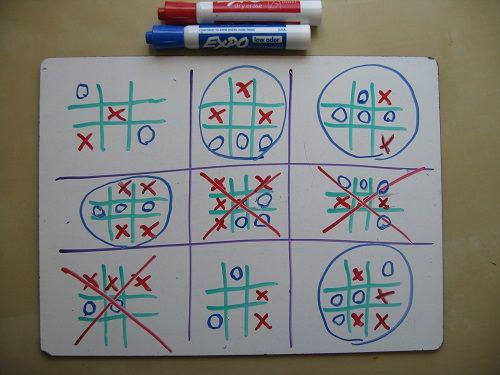
Need a couple of conventions:
What if my opponent sends me into a little box, which had already been defeated? It's an unfortunate situation. If there were blank cells, you have to choose one of them. Although affect the outcome of the game in this field you can not, you at least determine where to go will be your opponent.

What if my opponent sends me into a field filled? In this case, then congratulations - you can choose to turn any of the fields. (This means that you should avoid sending your opponent into a field filled!)
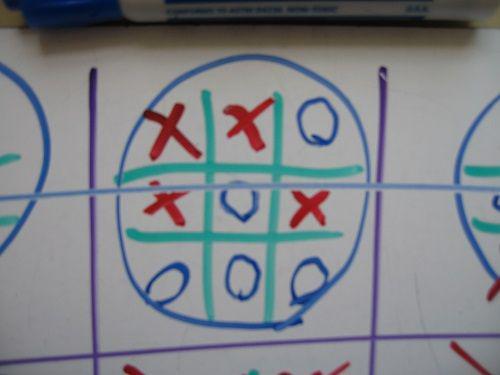
PS part (and stupid) question, "What if one of the smallest fields draw?" It seems that there are two options:
1. The field is considered to be not for the cross, nor for the toe. (So I play.)
2. The field is considered and the cross, and toe. (This will help avoid draws, although it may lead to strange nobody's when you and your opponent triumphed at the same time.)
I think each of the options work. Just make sure that you and your opponent have come to an agreement before the start of the game, as it affects the strategy.


298 One day I noticed a picnic mathematicians, crowding around the game of interest to which I expected the least: noughts and crosses.
You could themselves be noted that the game of noughts and crosses deadly boring. It is no place for a creative idea or sudden inspiration. Good players always play a draw.
But mathematicians at the picnic to play more sophisticated version of the game. In each of the cells on the square field, they drew a smaller field:

As the observation I noticed the basic rules:
Each turn is made in one of the small fields.

Reached in a small field location three identical pieces in a row wins this field.

To win the game you need to win in three small fields in a row.

But to understand the most important rule, it took me a while:
The player does not select one of the nine small fields, where he wants to go. The choice is determined by the previous move of your opponent. A cell in a small field in which it went - it's a small field where you have to make a move. (And the cells into which you go, in turn, determines how small field will walk your opponent.) For example, if I go here ...

Your next move you will make here ...

This gives the game an element of strategy. You can not afford to focus on a small field. You have to take into account is where your turn to send your opponent, and where to send you the next move, and so on.
The result looks very unusual. Players can move randomly, easily flowing design in two or three identical pieces in a row. But this madness is the order - they think through their moves in advance, keeping in mind the possibility to send the opponent in the pristine property. It is generally much more interesting than the usual tic-tac.

Need a couple of conventions:
What if my opponent sends me into a little box, which had already been defeated? It's an unfortunate situation. If there were blank cells, you have to choose one of them. Although affect the outcome of the game in this field you can not, you at least determine where to go will be your opponent.

What if my opponent sends me into a field filled? In this case, then congratulations - you can choose to turn any of the fields. (This means that you should avoid sending your opponent into a field filled!)

PS part (and stupid) question, "What if one of the smallest fields draw?" It seems that there are two options:
1. The field is considered to be not for the cross, nor for the toe. (So I play.)
2. The field is considered and the cross, and toe. (This will help avoid draws, although it may lead to strange nobody's when you and your opponent triumphed at the same time.)
I think each of the options work. Just make sure that you and your opponent have come to an agreement before the start of the game, as it affects the strategy.