644
New Horizons: a long way to the outskirts
After a series of news about the imminent (July 2015) the approximation of the interplanetary probe New Horizons to Pluto, I wanted to put together all the information about the trip unit for the past 8 years.
7 photos + text.

New Horizons was successfully launched January 19, 2006 from Cape Canaveral Atlas V rocket 551 with the upper stage Centaur and went to Jupiter to perform gravity assist.
It is worth noting that the rate of AMC after turning off the engine of the third stage was 46 km / c - it gave new horizons of the status of the fastest device has left Earth orbit. Currently, slightly less than the rate of the station 15 km / c, it loses Voyager 1, which is due to the maneuvers of Saturn accelerated to 17 km / s.

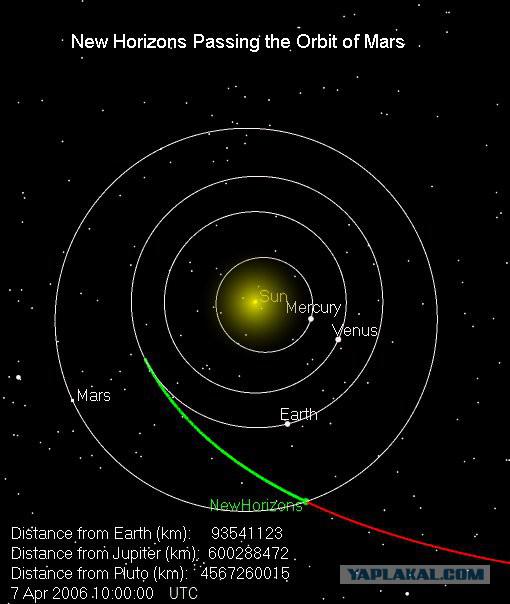
Less than four months New Horizons crossed the orbit of Mars (7 April 2006), at a distance of 299 million. Km. from the red planet. The speed of the device at this time was 21 km / c.
Next point of the mission - Jupiter, was reached on February 28, 2007. To obtain the required acceleration, AMC flew a distance of 2.3 million. Km. (3 times closer than Cassini flyby at the time) from Jupiter.

In addition to flexibility, the station has made more than 700 studies of the gas giant. Speed up to gravity assist - 23 km / s, after - 27 km / s.
Photos of Jupiter and Io (assembly) of the New Horizons

Saying goodbye to Jupiter, New Horizons was put into hibernation, and went to a lonely 8-year journey to its target - Pluto.
A year later (8 June 2008), AMC crossed the orbit of Saturn, while the planet itself was at a distance of 1.5 billion. Km. The rate at that time decreased to 18.26 km / s.
Uranus (distance to it - 1.8 billion. Km.), The unit crossed the March 18, 2011 at a speed of 15.75 km / s.
Now, on August 25, 2014, we are waiting for the intersection of the orbit of the last planet of the solar system - Neptune. Surprisingly, exactly 25 years ago, at the same time, Voyager 2 passed the first pictures of the planet and made many discoveries.
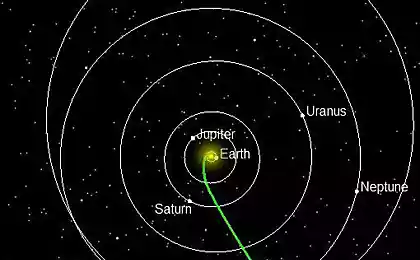
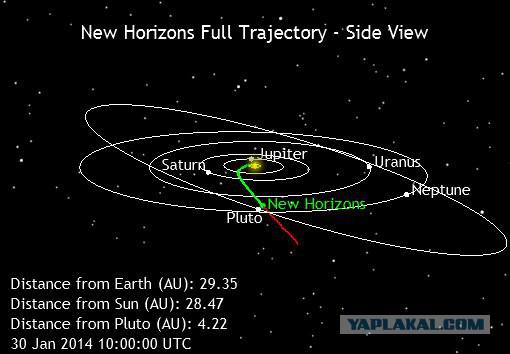
Now the station is at a distance of 28.47 AU from the Sun and is removed from it at a speed of 14.81 km / c. Daily tracking of "location" can be found at NASA.
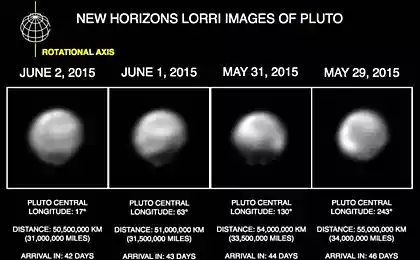
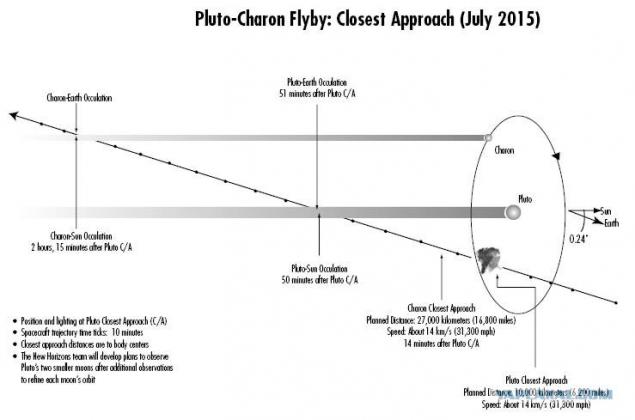
Already in the 10 weeks to the nearest approach (14 July 2015) NASA promises to show the first images of Pluto. Because of the high speed, New Horizons will stay near the planet for at least 3 hours (convergence with Charon, Pluto's moon, occurs within 14 minutes after reaching the nearest point of the orbit of Pluto), but the completion of data transfer over only 9 weeks since "apload" Earth is less than 800 bits \ s. The distance from the surface of Pluto will be 9600 km (camera resolution will allow to observe objects on the surface of up to 60 m), Charon - 27 thous. Km. An hour later, when the unit will go for the dark side of the planet, it will start to explore the atmosphere and try to find the ring.
Posted in [mergetime] 1392206654 [/ mergetime]
After completion of the New Horizons mission will go explore the Kuiper Belt objects, but what - is still unknown, scientists hope to find an object with a diameter of 100-150 km. The station is still able to create a color map of the object, analyze it for the presence of the atmosphere, satellites and rings.
It remains only to wish good luck to our travelers and wait for the opening of a new, unknown world.
Source:
7 photos + text.

New Horizons was successfully launched January 19, 2006 from Cape Canaveral Atlas V rocket 551 with the upper stage Centaur and went to Jupiter to perform gravity assist.
It is worth noting that the rate of AMC after turning off the engine of the third stage was 46 km / c - it gave new horizons of the status of the fastest device has left Earth orbit. Currently, slightly less than the rate of the station 15 km / c, it loses Voyager 1, which is due to the maneuvers of Saturn accelerated to 17 km / s.

Less than four months New Horizons crossed the orbit of Mars (7 April 2006), at a distance of 299 million. Km. from the red planet. The speed of the device at this time was 21 km / c.

Next point of the mission - Jupiter, was reached on February 28, 2007. To obtain the required acceleration, AMC flew a distance of 2.3 million. Km. (3 times closer than Cassini flyby at the time) from Jupiter.

In addition to flexibility, the station has made more than 700 studies of the gas giant. Speed up to gravity assist - 23 km / s, after - 27 km / s.
Photos of Jupiter and Io (assembly) of the New Horizons

Saying goodbye to Jupiter, New Horizons was put into hibernation, and went to a lonely 8-year journey to its target - Pluto.
A year later (8 June 2008), AMC crossed the orbit of Saturn, while the planet itself was at a distance of 1.5 billion. Km. The rate at that time decreased to 18.26 km / s.
Uranus (distance to it - 1.8 billion. Km.), The unit crossed the March 18, 2011 at a speed of 15.75 km / s.
Now, on August 25, 2014, we are waiting for the intersection of the orbit of the last planet of the solar system - Neptune. Surprisingly, exactly 25 years ago, at the same time, Voyager 2 passed the first pictures of the planet and made many discoveries.
Now the station is at a distance of 28.47 AU from the Sun and is removed from it at a speed of 14.81 km / c. Daily tracking of "location" can be found at NASA.

Already in the 10 weeks to the nearest approach (14 July 2015) NASA promises to show the first images of Pluto. Because of the high speed, New Horizons will stay near the planet for at least 3 hours (convergence with Charon, Pluto's moon, occurs within 14 minutes after reaching the nearest point of the orbit of Pluto), but the completion of data transfer over only 9 weeks since "apload" Earth is less than 800 bits \ s. The distance from the surface of Pluto will be 9600 km (camera resolution will allow to observe objects on the surface of up to 60 m), Charon - 27 thous. Km. An hour later, when the unit will go for the dark side of the planet, it will start to explore the atmosphere and try to find the ring.
Posted in [mergetime] 1392206654 [/ mergetime]
After completion of the New Horizons mission will go explore the Kuiper Belt objects, but what - is still unknown, scientists hope to find an object with a diameter of 100-150 km. The station is still able to create a color map of the object, analyze it for the presence of the atmosphere, satellites and rings.
It remains only to wish good luck to our travelers and wait for the opening of a new, unknown world.

Source: