Логика мышления. Часть 15. Консолидация памяти

Этот цикл статей описывает волновую модель мозга, серьезно отличающуюся от традиционных моделей. Настоятельно рекомендую тем, кто только присоединился, начинать чтение с первой части.

Попробуем представить информационную емкость мозга. Так как в основе памяти лежат нейроны, то для начала уточним, с каким количеством нейронов мы имеем дело. Наиболее точная оценка на сегодня, принадлежит Сюзанне Херкулано-Хузель (Frederico A.C. Azevedo, Ludmila R.B. Carvalho, Lea T. Grinberg, José Marcelo Farfel, Renata E.L. Ferretti, Renata E.P. Leite, Wilson Jacob Filho, Roberto Lent, Suzana Herculano-Houzel, 2009). По этой оценке на кору приходится 82% общей массы мозга и 19% от общего числа нейронов (рисунок ниже). По этой оценке кора состоит из порядка 16 миллиардов нейронов (1.6x10¹⁰).





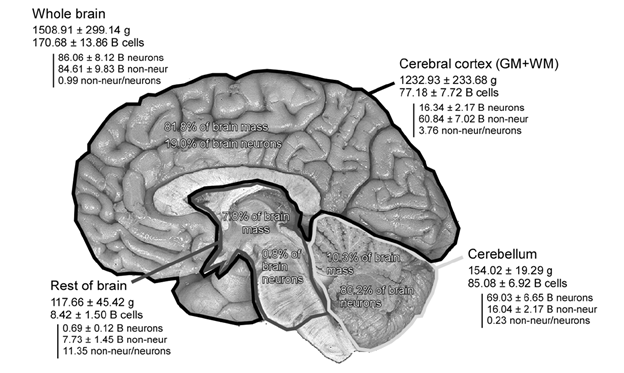
Количество нейронов в различных частях мозга (в миллиардах) (Frederico A.C. Azevedo, Ludmila R.B. Carvalho, Lea T. Grinberg, José Marcelo Farfel, Renata E.L. Ferretti, Renata E.P. Leite, Wilson Jacob Filho, Roberto Lent, Suzana Herculano-Houzel, 2009)

В моделях, использующих пластичность синапсов для объяснения природы памяти, емкость памяти считается достаточно просто. Характерное для нейрона количество синапсов – 10 000 (10⁴). Если полагать, что один синапс хранит один бит информации, то получается 1.6x10¹⁰ x 10⁴ = 1.6x10¹⁴ бит или приблизительно 2x10¹³ байт. Это около 20 000 гигабайт или 20 терабайт. Объем достаточно скромный даже по сегодняшним меркам.

Если предположить, что активная жизнь человека около 80 лет, из которых он треть проводит во сне, то это составит 80x365x(24-8)x60x60 = 1681920000 (1.7x10⁹) секунд. Получается, что если не учитывать организацию памяти, а просто заполнять ее в течение жизни, то можно позволить скорость записи 2x10¹³/1.7x10⁹=1.18x10⁴ байт/секунду или около 10 кбайт/секунду.

В нашей модели оценка объема памяти выглядит несколько иначе. Оценка синаптической памяти не меняется, те же 20 терабайт. Но это только память, хранящая образы нейронов-детекторов. Основные объемы приходятся на внесинаптические рецептивные кластеры. Если задаться оценкой, что один внесинаптический образ формируется из сигналов порядка 100 синапсов, то можно оценить информационную емкость одного элемента, как 100 бит. Исходя из оценки, что поверхность нейрона может содержать порядка 100 000 рецептивных кластеров, получаем емкость памяти 1.6x10¹⁰x10⁵x100 = 1.6 x10¹⁷ бит или 2x10¹⁶ байт. Что составляет 20 000 терабайт или 20 петабайт.

Если предположить, что половина этой памяти уходит на способность коры распространять волны идентификаторов, то объем событийной памяти можно оценить в 10 петабайт. Этот объем вызывает определенное уважение. Исходя из него, скорость записи информации при непрерывном запоминании может составлять 10¹⁶/1.7x10⁹=5.88x10⁶ байт/секунду или около 6 мегабайт/секунду. Если предположить, что фиксация энграмм происходит несколько раз в секунду, то можно дать оценку информационной емкости одной энграммы в районе 1 мегабайта.

Потенциально, наша память способна хранить достаточно детальное описание всего, что случается с нами в жизни. Тотальность памяти подтверждается наличием людей-феноменов, которые действительно «помнят все». Александр Лурия в результате многолетних наблюдений задокументировал один из примеров такой безграничной памяти:

«Оказалось, что память Ш. не имеет ясных границ не только в своем объеме, но и в прочности удержания следов. Опыты показали, что он с успехом – и без заметного труда – может воспроизводить любой длинный ряд слов, данных ему неделю, месяц, год, много лет назад. Некоторые из таких опытов, неизменно кончавшихся успехом, были проведены спустя 15 – 16 лет (!) после первичного запоминания ряда и без всякого предупреждения. В подобных случаях Ш. садился, закрывал глаза, делал паузу, а затем говорил: «да-да… это было у вас на той квартире… вы сидели за столом, а я на качалке… вы были в сером костюме и смотрели на меня так… вот… я вижу, что вы мне говорили...» – и дальше следовало безошибочное воспроизведение прочитанного ряда» (Лурия, 1968).

Но как бы не была безгранична наша память, хорошо известен тот факт, что гораздо легче и детальнее нам вспоминаются недавние события. Еще в 1885 году психологом Германом Эббингаузом была получена кривая забывания (Ebbinghaus, 1885)(рисунок ниже).



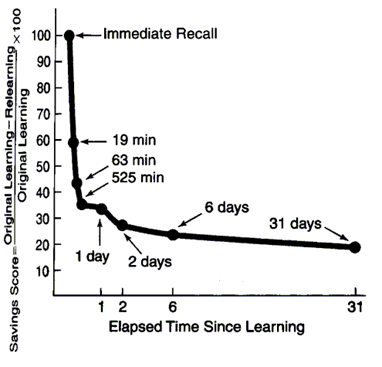
Кривая забывания

Наиболее резкое забывание наблюдается в первые минуты, затем процесс забывания замедляется. Через 30 дней память выходит на стабильную фазу, когда дальнейшего забывания не происходит. В своих опытах Эббингауз использовал наборы бессмысленных трехбуквенных слов, которые заучивал наизусть. Заучивание несколько отличается от простого восприятия, то есть кривая забывания для единожды услышанной фразы или увиденного образа будет несколько иная.

Запомнить что-либо более сильно позволяет повторение. Повторяя материал, мы не просто освежаем воспоминания и начинаем новый цикл забывания. После повторения, асимптота, на которую выходит кривая забывания, поднимается существенно выше по сравнению со своим предыдущим уровнем (рисунок ниже). Каждое новое повторение повышает шансы на то, что, спустя продолжительное время, нам удастся все относительно безошибочно вспомнить.



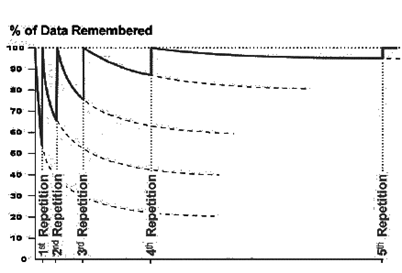
Кривая забывание при повторениях

Важно отметить, что повторение не обязательно должно сводиться к еще одному предъявлению заучиваемого образа. Воспоминание, достаточно точно воспроизводящее запомненное событие, так же является повторением. То есть чем чаще мы вспоминаем о чем-либо, тем прочнее оно врезается в нашу память.

Традиционная трактовка таких свойств памяти опирается на представление о переводе воспоминаний из кратковременной памяти в память долговременную. При этом часто, опираясь на компьютерные аналогии хранения данных, подразумевают перемещение информационных следов из одних частей мозга в другие. Так принято считать, что гиппокамп, работая наподобие оперативной памяти компьютера, накапливает текущие воспоминания, а затем перемещает их на кору, аналогично тому, как происходит сохранение компьютерных данных на долговременных носителях.

Процесс перехода воспоминаний из краткосрочной в долгосрочную форму принято называть консолидацией памяти. Это объективный и достаточно хорошо изученный процесс. Кроме того, что мы можем наблюдать изменения памяти на собственном опыте, есть и прямые подтверждения наличия консолидации. Так известно, что травмы головы, электрошок, судорога нарушают нормальный ход формирования памяти. Они вызывают ретроградную амнезию, когда воспоминания, относящиеся к некоторому промежутку времени, предшествующему сбою, оказываются утеряны.

Аналогичный эффект потери памяти получается при введении в мозг веществ, блокирующих экспрессию определенных генов, производящих белки, участвующие в работе памяти.

Кроме того, эффект ретроградной амнезии знаком многим по существенной потере памяти после чрезмерного употребления алкоголя. Определенная критическая доза выпитого спиртного настолько нарушает процесс консолидации, что часть воспоминаний полностью стирается, создавая невосполнимый провал в памяти. При этом происходит не потеря способности к текущему запоминанию, как при нарушениях в работе гиппокампа, а именно стирание уже полученных воспоминаний, точнее не перевод их в долговременную фазу хранения. Больной с синдромом Корсакова теряет воспоминание, как только происходит переключение его внимания. Человек, выпивший критическую дозу, все равно помнит недавние события, и во многих случаях может поддерживать связанную беседу. Однако наутро все воспоминания, начиная с определенного момента, оказываются стертыми.

Для объяснения эффекта консолидации необязательно замыкаться на компьютерной аналогии, связанной с физическим перемещением данных. В нашей модели консолидацию и ее смысл можно описать следующим образом. Как мы говорили ранее, внесинаптические метаботропные рецептивные кластеры обладают эффектом гистерезиса. Это значит, что если нейрон, генерирует спайк, то скачек мембранного потенциала при выполнении ряда условий, описанных нами ранее, может послужить поводом для перехода рецептивного кластера в устойчивое состояние. Устойчивое состояние – это либо состояние, в котором концевые части рецепторов вытолкнуты из мембраны и рецептор приобретает чувствительность к определенному сигналу, либо состояние их утопленности в котором рецептор, наоборот чувствительность теряет. Такое изменение происходит с рецептивными кластерами, для которых выполнилось условие интерференции медиаторов от окружающих их синапсов, то есть которые настроились на определенный образ.

Переход рецептивных кластеров в такое состояние происходит одновременно у огромного количества нейронов, активных в текущий момент времени. Что означает, что этот текущий момент запоминается с чрезвычайной избыточностью и детализацией. Это ведет к тому, что при прочих равных, текущие события имеют значительно более высокую вероятность быть вспомненными по сравнению с событиями более отдаленными во времени.

Такую гиперподробную память можно назвать оперативной или кратковременной памятью, но не стоит путать ее с текущей вызванной и волновой активностью нейронов коры. Активность нейронов формирует описание происходящего, кратковременная же память хранит картины таких относительно недавних состояний. Причем кратковременная память ничем не отличается от остальной памяти, за исключением того, что свежие воспоминания более детальны, так как используют существенно большее количество рецептивных кластеров, чем остальные энграммы.

Продолжительность сверхоперативной памяти – секунды. Затем большая часть внесинаптических рецепторов возвращается в исходное состояние, обретая готовность участвовать в новых актах запоминания. Но существенная часть рецептивных кластеров по тем или иным причинам остается в состоянии фиксации образа. Они переходят в следующую устойчивую фазу, которая позволяет им существовать дальше и соответственно хранить фрагмент своего воспоминания.

Можно предположить, что каждое воспоминание проходит несколько стадий консолидации, лишаясь на каждом этапе части своих рецептивных кластеров. Самый простой алгоритм забывания – вероятностный. Регулируя вероятность прохождения рецептивным кластером очередного этапа консолидации, можно получить требуемый объем для каждого воспоминания к моменту его перехода в долговременную память.

Фазы консолидации сопровождается синтезом советующих белков, которые определяют общее течение всех процессов. Ход консолидации для метаботропных и для ионотропных рецепторов имеет свои особенности, но достаточно похож идеологически. Сразу после обучения в ядре нейрона начинается экспрессия немедленных «ранних генов». Эти гены кодируют транскрипционные факторы. Транскрипционные факторы запускают транскрипцию «поздних генов». Примерный график такой процедуры показан на рисунке ниже.



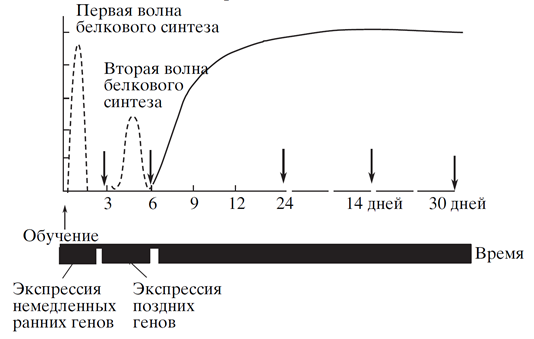
Экспрессия «ранних» и «поздних» генов (Е.В. Муравьева, К.В. Анохин, 2006).

Известны разные белки, относительно которых доказано их участие в процессе формирования памяти. Arc, CPEB, Kibra – это только малая часть из них, хотя и наиболее часто упоминаемая. Надо помнить, что информация оставляет на нейроне два типа следов. Один связан с изменением чувствительности его синапсов, другой с фиксацией изменений во внесинаптических рецепторах. Первое влияет на свойства нейрона, как детектора. Второе обеспечивает способность нейронов распространять волны идентификаторов, хранить событийную память, формировать ассоциативность и тому подобное. Как и в какой последовательности происходит белковая регуляция этих процессов вопрос не простой и пока не имеющий общепринятого ответа, поскольку нет пока и общепризнанной модели памяти. Поэтому в нашей модели мы будем делать акцент на общую идеологию процессов, к сожалению, не имя возможности доказательно описать их белковую регуляцию.

Консолидация фактически задает таймер, который отсчитывает стадию жизни элементов воспоминания и регулирует вероятность их перехода в следующую фазу. Можно предположить, что повторение опыта или что равносильно воспоминание о нем, изменяют ход консолидации, повышая шансы рецептивных кластеров на переход в фазу долговременной памяти. То есть чем больше повторений или чем чаще воспоминания, тем более значимый след оставляет событие. И тем выше вероятность его восстановления при соответствующем информационном запросе.

Так как события эмоционально значимые заставляют нас чаще вспоминать о них, по сравнению с событиями нейтральными, то это может быть одной из причин, почему эмоционально окрашенные события формируют более прочные и устойчивые следы в нашей памяти.

Но воспоминания о пережитом опыте не так просты, как кажутся. Психологам давно известен феномен трансформации воспоминаний. Первым его показал еще в 1932 году Фредерик Бартлетт (Bartlett, 1932). Он установил, что если человек, вспоминая определенное событие, добавляет какие-либо детали, то исходное воспоминание замещается новым, а измененные детали становятся частью этого нового воспоминания. Причем человек не осознает этих изменений, а считает, что все было именно так как он помнит теперь. Такое изменение воспоминаний принято называть реконсолидацией памяти.

Реконсолидация памяти хорошо вписывается в нашу модель. Воспоминание о каком-либо событии сопровождается восстановлением его уникального идентификатора. Если по какой-либо причине происходит искажение исходного воспоминания, то текущий информационный образ запоминается с тем же самым идентификатором, что и основное воспоминание, так как именно этот идентификатор присутствует в пространстве коры. А значит, неизбежно происходит описанный Барлеттом феномен трансформации.

Есть очень интересные опыты, которые показывают, что реконсолидация может сопровождаться не только трансформацией, но и стиранием памяти. Но поскольку эти опыты больше относятся к поведению, чем к событийной памяти мы рассмотрим их позже в соответствующем разделе.

Общую идеологию событийной памяти можно описать следующим образом. Поступающая информация создает свежие воспоминания с огромной избыточностью и детализацией. Это делает их исключительно доступными для оперативного доступа. Такая память живет не долго. Она память подвергается стадиям консолидации, каждая из которых уменьшает количество рецептивных кластеров, формирующих энграммы. В результате всех этапов консолидации, продолжающихся, по-видимому, около месяца, энграммы приобретают стабильный объем и переходят в фазу долговременного хранения.

Ранее мы оценили порядок объема событийной памяти мозга в 10 петабайт. Откуда цыганским методом вывели оценку размера энграммы в 1 мегабайт. Эта оценка может быть справедлива для старых, прошедших все стадии консолидации, воспоминаний. Большая часть информации, с которой мы оперируем, относится к текущему дню. Для этой информации обеспечивается развернутое избыточное хранение. Можно предположить, что такая актуальная память занимает существенный объем от общей памяти мозга. Если бы я был конструктором человеческого мозга, то я бы эмпирически отвел на свежие воспоминания половину всей доступной памяти, а оставшуюся половину определил под старые воспоминания.

При таком эмпирическом предположении скорость записи информации мозгом можно оценить, как 5x10¹⁵/(16x60x60), что составляет около 10¹¹ байт или 100 гигабайт в секунду. Конечно, это значительно больше, чем весь объем информации, поступающий от всех вместе органов чувств. Но разговор идет не о входном объеме, а о развернутом описании, состоящем из множества описаний, возникающих на каждой из зон коры.

В такой прикидке начальный размер одной энграммы составит порядка 10 гигабайт. Собственно, процесс консолидации памяти – это постепенное сведение этого чрезвычайно избыточного объема до уровня порядка 1 мегабайта.

Тем не менее, каким бы на самом деле не было соотношение объемов новой и старой памяти, природа должна была оптимизировать его так, чтобы не допустить неоправданного резервирования простаивающих объемов. Это значит, что с учетом крайне высокой скорости записи текущей информации, может наступить момент переполнения всей доступной памяти. Можно предположить, что сонливость – это и есть состояние, когда информационные ресурсы мозга подходят к своему заполнению, и требуется расчистка памяти.

В принципе, оперативная консолидация памяти происходит постоянно, непрерывно сжимая объемы энграмм, мозг обеспечивает пространство для новых воспоминаний. Но можно предположить, что оперативная консолидация имеет ряд недостатков. Так в нашей модели нейроны-детекторы образуют паттерны, соответствующие понятиям. Каждое понятие образуется множеством паттернов, расположенных в разных местах коры. Чтобы паттерн запустил волну, должна активироваться существенная часть нейронов паттерна. Это значит, что если пользоваться вероятностной консолидацией, просто удаляя часть рецептивных кластеров, то мы постепенно разрушим все энграммы до такого уровня, когда ни один из паттернов не будет в состоянии излучить волну, связанную с этим воспоминанием. Чтобы избежать этого, разумно использовать выборочную консолидацию.

Выборочная консолидация предполагает, что мы избирательно определяем на каких паттернах стоит оставить четкие следы воспоминаний, а на каких стоит их полностью удалить. Тогда при том же объеме энграммы и сохранении ее распределенного характера удастся избежать малой плотности энграмм на отдельных паттернах.

Можно предположить, что выгоднее использовать для сохранения энграмм те паттерны, которые своим положением на коре наиболее точно соответствуют активности, связанной с общим контекстом воспоминания. Но процедура определения таких паттернов требует повторного технического воспроизведения запомненных событий. Однако такое воспроизведение несовместимо с нормальной работой мозга, так как, протекая одновременно с текущим восприятием, будет восприниматься мозгом как галлюцинация. Уместно предположить, что оптимальная консолидация, связанная с удалением большей части, накопленной за день информации, не возможна или затруднена при обычной работе мозга. Тогда получается, что сон – это именно то состояние, которое необходимо мозгу для выполнения процедур подобного рода.

Кроме того, что мозг накапливает событийные воспоминания, одновременно с этим происходит обучение нейронов, как детекторов. И то и другое основано на изменении структуры нейронных рецепторов. Изменения в рецепторах управляются продуктами экспрессии определенных генов. Продукты экспрессии генов – это белки. Часть из них непосредственно участвует в клеточных процессах, часть является транскрипционными факторами, которые регулируют последующую экспрессию генов. По изменению концентрации соответствующих белков можно судить о течении процессов, связанных с обоими видами консолидации.

Увидеть и оценить концентрацию белков можно через окрашивание среза мозговой ткани красителем, избирательно реагирующим на требуемый белок. Подобные наблюдения показали, что наиболее масштабные изменения происходят именно во время сна (Chiara Cirelli, Giulio Tononi, 1998) (Cirelli, 2002) (рисунки ниже).



Распределение белка Arc в теменной коре крысы после трех часов сна (S) и после трех часов спонтанного бодрствования (W) (Cirelli, 2002)



Распределение транскрипционного фактора P-CREB в корональных участках теменной коры крысы после трех часов сна (S) и в случае лишения сна на три часа (SD) (Cirelli, 2002)

Консолидация памяти во сне происходит в несколько этапов. У здорового человека сон начинается с первой стадии медленного сна, которая длится 5-10 минут. Затем наступает вторая стадия, которая продолжается около 20 минут. Еще 30-45 минут приходится на периоды третей и четвертой стадий. После этого спящий снова возвращается во вторую стадию медленного сна, после которой возникает первый эпизод быстрого сна, который имеет короткую продолжительность — около 5 минут. Во время быстрого сна глазные яблоки очень часто и периодически совершают быстрые движения под сомкнутыми веками. Если в это время разбудить спящего, то в 90% случаев можно услышать рассказ о ярком сновидении. Вся эта последовательность называется циклом. Первый цикл имеет длительность 90-100 минут. Затем циклы повторяются, при этом уменьшается доля медленного сна и постепенно нарастает доля быстрого сна, последний эпизод которого в отдельных случаях может достигать 1 часа. В среднем при полноценном здоровом сне отмечается пять полных циклов.

Стадии сна можно объяснить необходимостью обработать информацию различного типа. Алгоритмы консолидации событийной памяти, волновой памяти, связанной с распространением идентификаторов, и памяти, связанной с пластичностью синапсов, могут сильно различаться.

В наших предположениях хорошо объясняется цикличность сна. Полная консолидация, как каждому известно из личного опыта, требует около восьми часов. Но обстоятельства могут заставить нас проснуться раньше. Если бы восьмичасовой сон состоял из одного цикла, разделенного на несколько фаз, то преждевременное прерывание сна вело бы к тому, что начальные фазы сна успевали бы завершиться полностью, при том, что поздние еще даже не начинались. То есть часть информации оставалась бы совершенно необработанной, при этом полностью исчерпав за предыдущий день соответствующий ресурс мозга. То есть мозг, по сути, был бы в неработоспособном состоянии. Несколько циклов позволяют при преждевременном пробуждении хотя бы частично выполнить каждую из процедур консолидации и привести мозг в адекватное состояние. Но потребность в полноценной консолидации не исчезает, и впоследствии мозг должен будет компенсировать упущенные циклы более продолжительным сном, что обычно называется «отоспаться».

Похоже, что консолидация памяти связана с фазами медленного сна. По мере ее завершения эти фазы становятся все короче, уступая место быстрому сну. Это объясняет тот факт, что при полном завершении консолидации, завершающий этап сна состоит исключительно из продолжительной фазы быстрого сна.

Быстрый сон – это те самые сновидения, которые образуют причудливые фантазии, только отдаленно связанные с реальным опытом. Закономерность, подмеченная для сновидений еще Зигмундом Фрейдом, гласит, что во сне проступают явления, наиболее беспокоящие нас, важные для нас, концентрирующие суть наших терзаний и переживаний (Фрейд, 1900). В большинстве случаев сны очень быстро забываются. Мы видим сны каждую ночь, но стремительность, с которой мы их забываем, заставляет многих считать, что они вообще не видят снов.

В нашей модели стирание сновидений реализуется достаточно просто. Для этого достаточно сделать так, чтобы следы идентификаторов гиппокампа не фиксировались надолго, а подвергались быстрому расформированию. Это приведет к тому, что мы будем безвозвратно забывать о сновидениях. Но если, проснувшись, мы успеем вспомнить о недавнем сне, то возникнет новое уже традиционное воспоминание, которое сохранит события сна.

Можно предположить, что для снов стирание следов идентификаторов гиппокампа не сопровождается удалением ассоциативных следов. Тогда смысл сновидений можно объяснить усилением системы ассоциаций для наиболее значимых и важных для нас понятий. Что в свою очередь способствует последующему восприятию мира таким образом, что именно эти понятия будут наиболее акцентированы в системе описания новых событий.

Всем хорошо известно, что «утро вечера мудренее». Но в чем суть этой мудрости? Иногда утренние озарения объясняют тем, что де, мол, мозг ночью решает дневные задачи. К такому объяснению подталкивает, во-первых, тот факт, что зафиксированная во многих исследованиях ночная активность мозга сильно напоминает активность пережитого днем, а, во-вторых, созвучность сновидений тем темам, что нас тревожат наяву. Но уместней предположить, что мозг не решает ночью дневные задачи, он работает над оптимизацией системы понятий и воспоминаний. Утром эта оптимизация позволяет значительно легче найти объяснения вчера еще непонятным вопросам. Чтобы правильно задать вопрос, надо знать большую часть ответа. Та работа, которую делает ночью мозг — это и есть подготовка той самой большей часть ответа — возможности подойти к вопросу с «правильным» набором внутренних понятий и избавившись от излишней детальности ненужных воспоминаний. То есть, если все, сказанное сейчас про сон, кажется вам слишком туманным, то попробуйте вернуться к этому завтра.

Нет смысла жалеть о времени, проведенном во сне. Сон – это замечательная возможность «поумнеть», не прикладывая никаких усилий. Единственное, что все-таки необходимо – это предварительно загрузить голову достаточным объемом свежей информации. Причем этой информацией могут быть не только новые факты, но и старые знания, заново вспомненные или обдуманные. Любые наши размышления оставляют след свежих воспоминаний на коре. Во сне происходит консолидация новых размышлений и старого опыта, что дает возможность возникнуть более глубоким обобщениям. Это означает, что дневные размышления по какому-либо вопросу имеют смысл, даже если они не приводят к немедленному ответу. Эти размышления создают те свежие воспоминания, относящиеся к интересующей нас теме, что ночью дадут мозгу возможность поработать над оптимизацией всей системы наших понятий. Можно вспомнить о том, что маленькие дети, у которых организация коры идет наиболее активно, вообще, большую часть времени проводят во сне.

Идеи консолидации позволяют объяснить не только сон младенцев, но и консерватизм стариков. Под консерватизмом мы понимает отказ от новых идей и навыков при условии сохранения нормальной событийной памяти. В традиционных подходах это вызывает определенное противоречие. Казалось бы, способность запоминать новые факты должна обеспечивать способность обучаться новым принципам и осваивать новые навыки. Но все встает на место, если вспомнить, что есть организация нейронов-детекторов, формирующая набор понятий мозга, а есть событийная память, описывающаяся и хранящаяся на базе этих понятий. Ежедневная консолидация событийной памяти расчищает, по-видимому, больше половины доступного объема. Это значит, что независимо от возраста событийная память может быть крепкой, если этому не мешают органические нарушения. Но вот с нейронами-детекторами все обстоит сложнее. Похоже, что с возрастом количество нейронов, определившихся со своей специализацией, становится все больше, и для образования новых понятий остается все меньше и меньше возможностей. И тогда мы приходим к ситуации, что запомнить мы можем все, но только в тех понятиях, которые у нас существуют. А вот сформировать новые понятия мы уже можем с трудом или не можем вообще. Соответственно, все принципиально новое вызывает трудности восприятия и естественное отторжение, что и называется старческим консерватизмом.

Использованная литература

Предыдущие части:
Часть 1. Нейрон
Часть 2. Факторы
Часть 3. Персептрон, сверточные сети
Часть 4. Фоновая активность
Часть 5. Волны мозга
Часть 6. Система проекций
Часть 7. Интерфейс человек-компьютер
Часть 8. Выделение факторов в волновых сетях
Часть 9. Паттерны нейронов-детекторов. Обратная проекция
Часть 10. Пространственная самоорганизация
Часть 11. Динамические нейронные сети. Ассоциативность
Часть 12. Следы памяти
Часть 13. Ассоциативная память
Часть 14. Гиппокамп

Алексей Редозубов (2014)

Источник: habrahabr.ru/post/216633/