Si tienes hasta siete pulgadas en la frente, no podrás recordar todo lo impreso en libros, necesitas desarrollar el pensamiento lateral.

Hoy ofrecemos una prueba para probar lo bien que los lectores desarrollan la creatividad y el pensamiento no estándar. No será fácil pasar. Tendrás que apartarte de la senda golpeada. Y sólo esas formas de resolver problemas que solíamos ignorar serán útiles.



Por cierto, este enfoque tiene una base científica. El psicólogo británico Edward de Bono lo llamó pensamiento lateral (lateral). Según Bono, la creatividad no es un talento, sino una habilidad que se puede aprender y desarrollar. Complementado con pensamiento lateral, ayuda a alcanzar metas, evitando métodos convencionales y convencionales.

Pensamiento no convencional

1. ¿Con qué número debe reemplazarse la marca de preguntas?
   
   
   
   a) 24
   b) 27
   c) 56
   g) 92
   
   
2. Estoy listo para revelar mis secretos a cualquiera. Pero no escucharás ni una palabra de ella. Resolver el rompecabezas y elegir la opción con el número de letras en la palabra deseada.
   4
   b) 5
   c) 6
   g) 8
3. ¿Qué tienen estas imágenes en común? ¿Con qué letra termina la respuesta?
   
   
   
   a) Y
   b) E
   c) Y
   d) S
   
   
4. ¿Cómo podría ser que la mitad de los 12 eran 7? La decisión está relacionada con...
   a) División
   b) figuras de otro modo
   c) resta
5. Incluso el maestro del juego “¿Qué?” no pudo responder esta pregunta. ¿Dónde? ¿Cuándo? Alexander Druz. ¿Qué número debería estar en la plaza de aparcamiento donde se encuentra el coche?
   
   
   
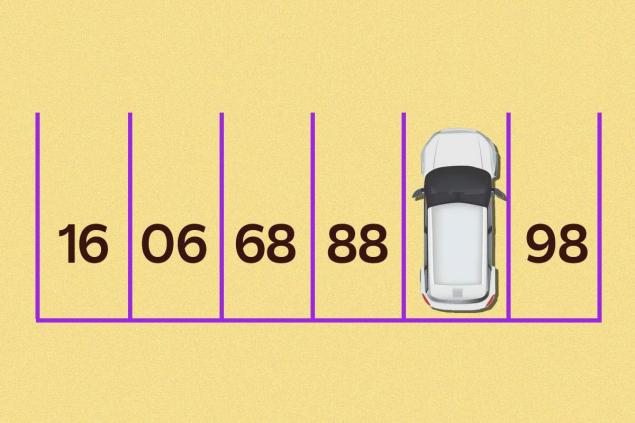
   a) 96
   b) 94
   c) 90
   g) 87
   
   
6. ¿Cuál es la cifra extra?
   
   
   
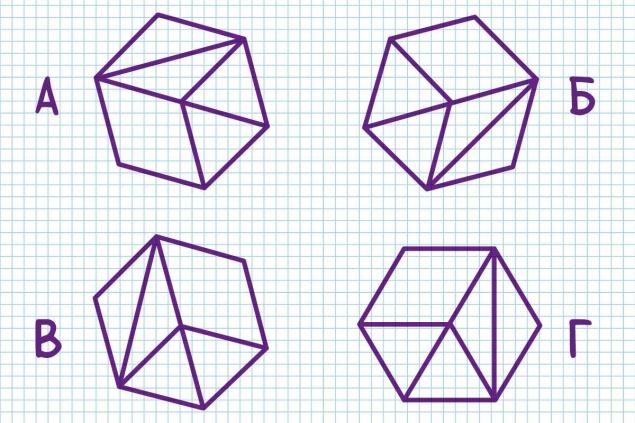
   a) Y
   b) B.
   c) En
   g) G
   
   
7. Un ángulo de 1 grado se considera en una lupa, que tiene una magnificación de 8 veces. ¿Qué ángulo de tamaño será visible en esta lupa?
   1 grado
   b) 2 grados
   c) 8 grados
   g) 16 grados
8. ¿Qué número debe estar en el lugar de la marca de preguntas?
   
   
   
   a) 2
   b) 3
   c) 8
   g) 504
   
   
9. El mobiliario se come al final del almuerzo. ¿Qué respuesta terminará esta secuencia: snack, sopa, ensalada, segundo curso...
   
   
   
   Cuadro
   pan
   menú
   d) postre
   
   
10. Encuentra un patrón para reemplazar la marca de preguntas con un número.
    Washington - 162
    Chicago - 54
    Richmond - 70
    Boston...

Respuestas.

1. Encontrar el último número en cada fila no es fácil. Para ello, es necesario dividir los números segundo y tercero de la serie por 2. Y luego multiplicar el primer número y los dos resultantes.
   Por ejemplo, para la primera fila será
   3 * (8:2) * (6:2) = 36
   En consecuencia, para la última fila
   9 * (6:2) * (2:2) = 27.
2. El libro. 5 cartas.
3. Lo que estas imágenes tienen en común es marco. Escogemos una carta de aquí. Y.
4. Escriba el número 12 en números romanos: XII. A continuación, dibuja una línea en el medio. La mitad superior parecerá un VII.
5. La cuestión, de hecho, es bastante infantil, pero requiere una solución inusual. Tienes que mirar la foto desde el otro lado. Entonces queda claro que el coche está en el estacionamiento con el número 87.
6. B. Todos los demás son iguales, sólo invertidos.
7. La inclinación de las líneas relativas entre sí no cambiará con el aumento. El ángulo de un grado seguirá siendo así.
8. Todas estas palabras tienen letras que se utilizan en el sistema numeral romano. Bien, palabra A.VIATOR se puede ver en Romano 6 (VI). Ya no es difícil, sólo tienes que saber que D es el 500 romano. IX = 9, I = 1, y DIV = 504.
9. La respuesta correcta sería el postre. Pero la primera parte de la pregunta indica que es una tabla.
10. La regularidad consiste en multiplicar el número de cartas vocales por el número de consonantes y el número total de letras. Boston: 2 vocales, 4 consonantes y sólo 6 letras. De aquí tenemos 2 * 4 * 6 = 48..

Nuestros ejemplos no estándar le ayudarán a pasar tiempo con beneficio. Después de todo, el ingenio ayuda a buscar soluciones inusuales, interesantes y sencillas, logrando resultados no sólo en el juego, sino también en la vida real de la manera más corta posible.