728
20 gifok que explican las matemáticas en los dedos
No seque cuadros y figuras, que a veces son imposibles de entender. Está claro que cada imagen visual de las leyes básicas de las matemáticas - y mucho está claro
.
Mira interesante incluso para aquellos que no entendía.
1. Cómo dibujar una elipse:

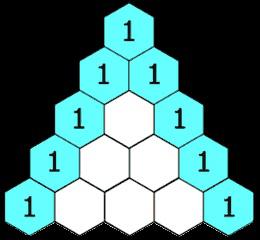
2. ¿Cómo triángulo de Pascal (en la parte superior y en los lados - uno, cada número es la suma de los números que les impone):
3. ¿Qué tan rápido se multiplican binomio:
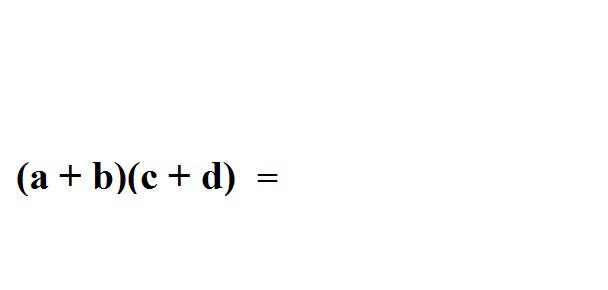
4. ¿Cómo entender los logaritmos:

5. ¿Cómo no se pierda, la celebración de la transposición de la matriz:

6. Intuitivamente, que "los pantalones de Pitágoras todos los lados son iguales»:

7. ¿Por qué es la cantidad de ángulos externos del polígono es siempre 360 grados:
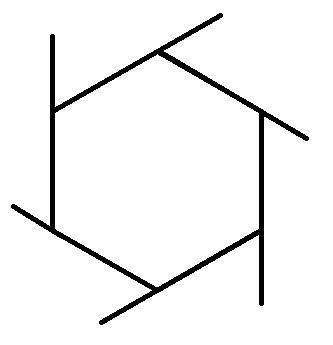
8. ¿Cómo se ve realmente como el número π:
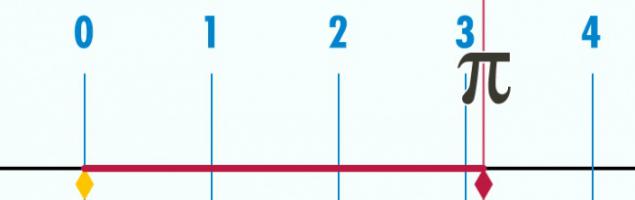
9. Si la longitud del arco es igual a a lo largo de la longitud de su radio, el ángulo resultante es igual a un radián:
10. Visualización sinusal (rojo) y el coseno (azul) ángulo:
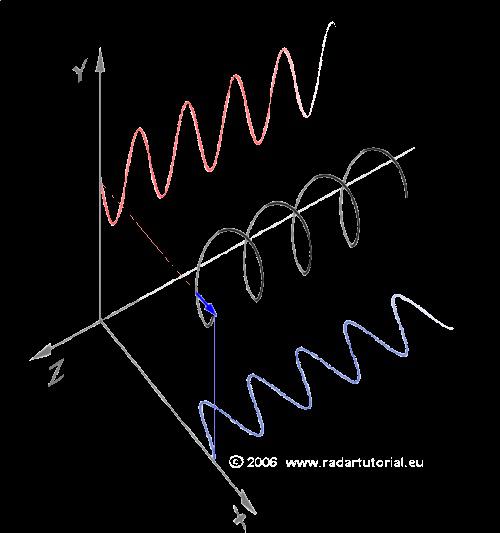
11. Lo mismo, pero aún más simple:
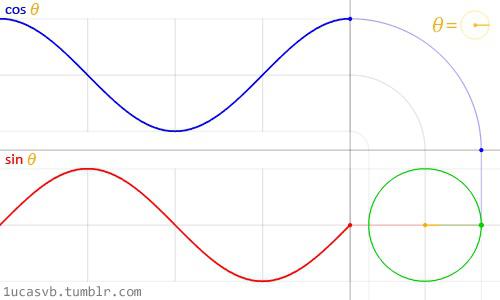
12. Los mismos triángulos:
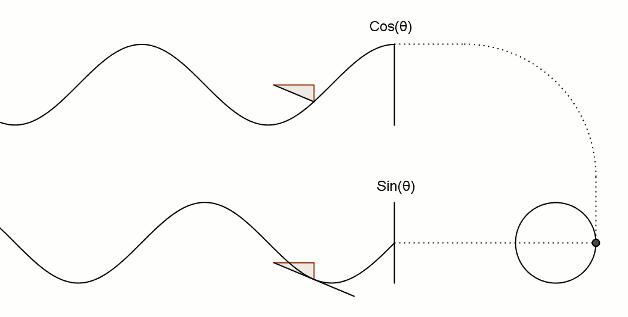
13. Y un poco de trigonometría:
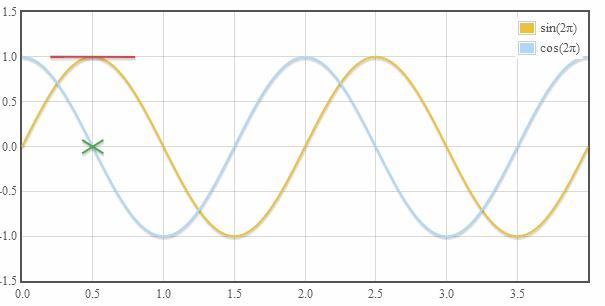
14. Curvas tangente:
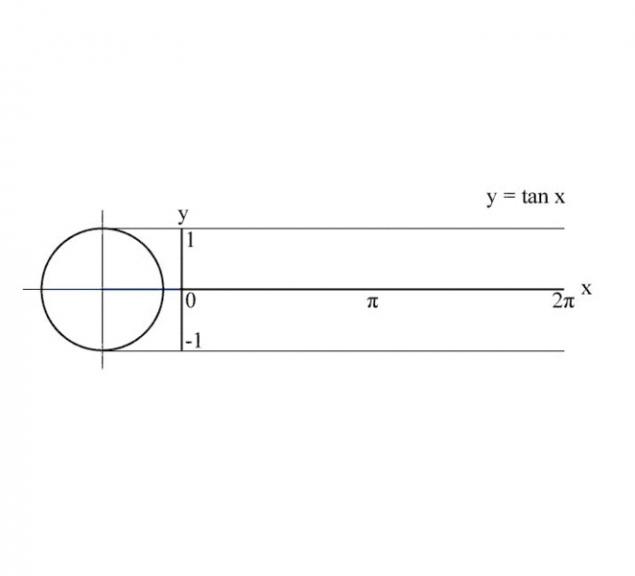
15. Si expande la imagen se vuelve aún más claro:
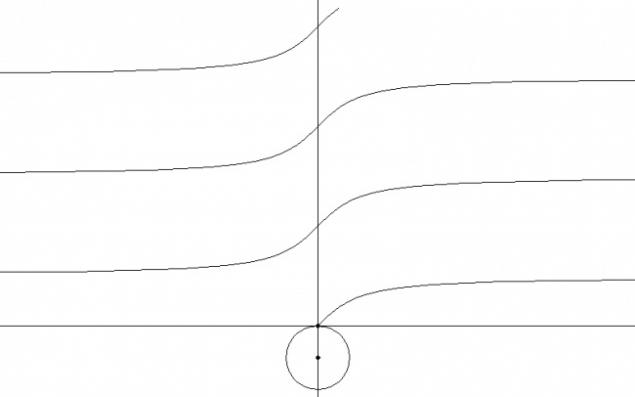
16. ¿Cómo puedo transferir la función del sistema cartesiano de coordenadas polares:
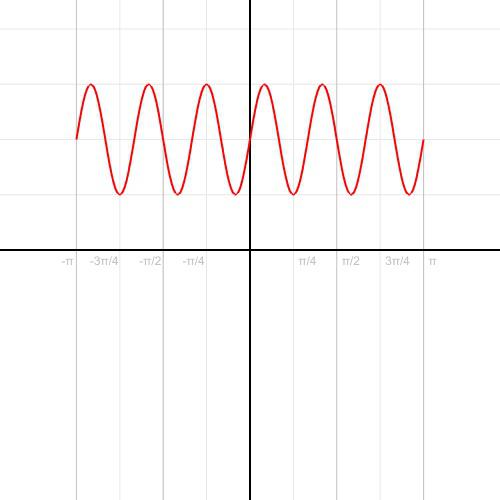
17. Cómo dibujar una parábola:
18. Sumas de Riemann - el área aproximada bajo la curva:
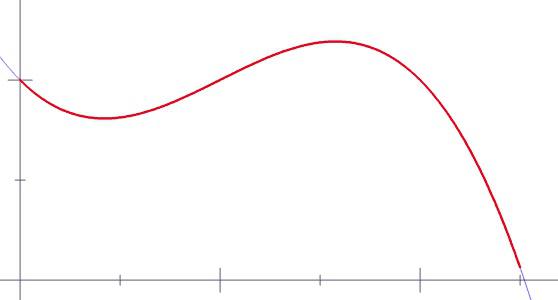
19. Cómo dibujar una hipérbole:

20. Si traducimos esto en 3D, se hiperboloide
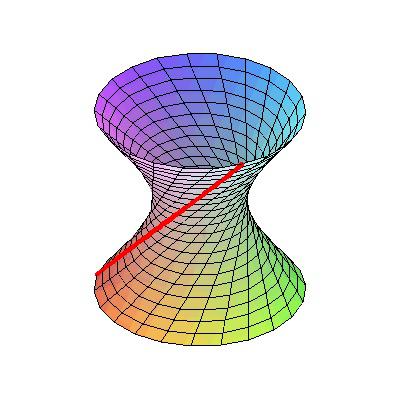
21. Así es como se ve en la vida real:

Ver también:
Magia química Lo que los científicos están bromeando
100 cursos gratuitos en línea en
rusa
a través de ain.ua/2014/08/28/538268?utm_content=buffer94cd8&utm_medium=social&utm_source=plus.google.com&utm_campaign=buffer
.
Mira interesante incluso para aquellos que no entendía.
1. Cómo dibujar una elipse:

2. ¿Cómo triángulo de Pascal (en la parte superior y en los lados - uno, cada número es la suma de los números que les impone):

3. ¿Qué tan rápido se multiplican binomio:
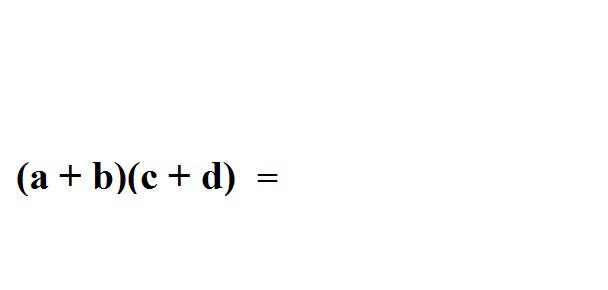
4. ¿Cómo entender los logaritmos:

5. ¿Cómo no se pierda, la celebración de la transposición de la matriz:

6. Intuitivamente, que "los pantalones de Pitágoras todos los lados son iguales»:

7. ¿Por qué es la cantidad de ángulos externos del polígono es siempre 360 grados:

8. ¿Cómo se ve realmente como el número π:

9. Si la longitud del arco es igual a a lo largo de la longitud de su radio, el ángulo resultante es igual a un radián:

10. Visualización sinusal (rojo) y el coseno (azul) ángulo:

11. Lo mismo, pero aún más simple:

12. Los mismos triángulos:

13. Y un poco de trigonometría:

14. Curvas tangente:

15. Si expande la imagen se vuelve aún más claro:

16. ¿Cómo puedo transferir la función del sistema cartesiano de coordenadas polares:

17. Cómo dibujar una parábola:
18. Sumas de Riemann - el área aproximada bajo la curva:

19. Cómo dibujar una hipérbole:

20. Si traducimos esto en 3D, se hiperboloide

21. Así es como se ve en la vida real:

Ver también:
Magia química Lo que los científicos están bromeando
100 cursos gratuitos en línea en
rusa
a través de ain.ua/2014/08/28/538268?utm_content=buffer94cd8&utm_medium=social&utm_source=plus.google.com&utm_campaign=buffer