436
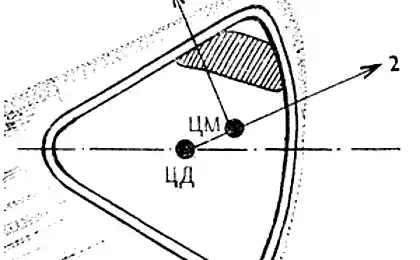
五部分地,其中对象可以在旋转坐标系中实现完全不动的
我们正在寻找停车其他planet
你可能已经听说过拉格朗日点 - 这个星球的地球和月亮的力量,作用于对方绕了五重力稳定点。这是卫星的理想场所。由于这个令人难以置信的模式,你可以确切地知道他们在哪里,以及为什么。
拉格朗日点不仅是地球。科幻作家经常使用他们在自己的作品,其中飞船飞行员需要一个良好的,稳定的地方接近挂到地球或月亮。拉格朗日点 - 它可能是在太空中,在那里你可以抛锚最近的地方
。
布赖恩·温斯坦,应用数学导致了不起的博客«Fouriest系列»在不倒翁的研究生,汇集了围绕地球的拉格朗日点的一个令人印象深刻的例子。这里是你所看到的他的解释:
“拉格朗日点 - 的五个地方在眼窝系统,其中,两个大群众的引力的组合被精确地通过增加旋转坐标系的离心力来补偿。在这五点上的第三体(低重量)的力的净力为零,允许所述第三主体是完全静止的相对于该两个质量块。这就是为什么如果你把第三体在这些点中的一个,它会保持完全不动的旋转框架。
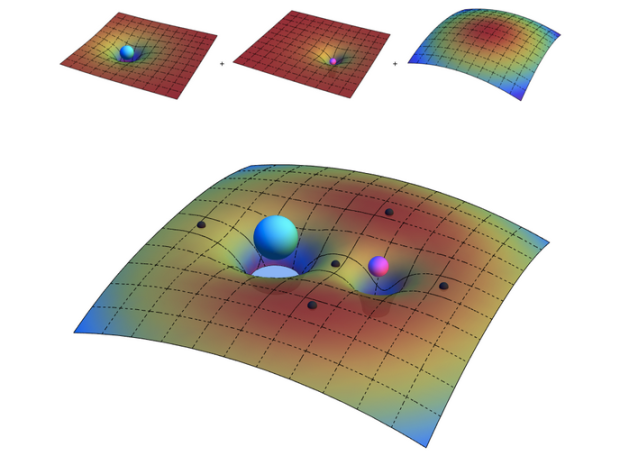
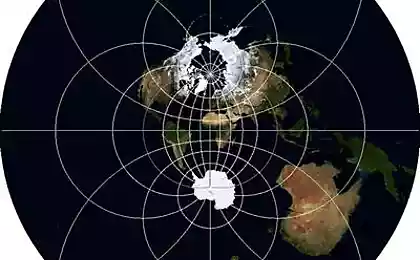
图像示出了具有第一质量,第二质量和旋转坐标系统相关联的区域。如果你把它们放在一起,这些区域形成的演技领域。这五个拉格朗日点用灰色区域表示。
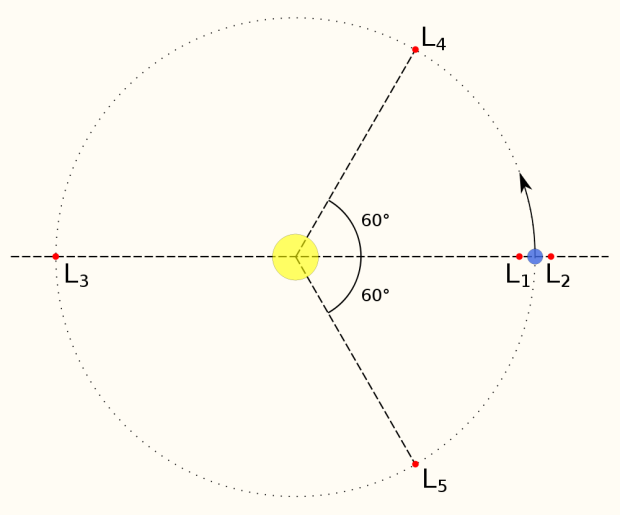
前三拉格朗日点(表示为L1,L2和L3)被布置在一行中有两个大的机构和处于亚稳状态。 L4和L5被设置在在前面所述第二主体上的轨道和后部60°的角度,并处于稳定状态»。
通过factroom.ru

你可能已经听说过拉格朗日点 - 这个星球的地球和月亮的力量,作用于对方绕了五重力稳定点。这是卫星的理想场所。由于这个令人难以置信的模式,你可以确切地知道他们在哪里,以及为什么。
拉格朗日点不仅是地球。科幻作家经常使用他们在自己的作品,其中飞船飞行员需要一个良好的,稳定的地方接近挂到地球或月亮。拉格朗日点 - 它可能是在太空中,在那里你可以抛锚最近的地方
。

布赖恩·温斯坦,应用数学导致了不起的博客«Fouriest系列»在不倒翁的研究生,汇集了围绕地球的拉格朗日点的一个令人印象深刻的例子。这里是你所看到的他的解释:
“拉格朗日点 - 的五个地方在眼窝系统,其中,两个大群众的引力的组合被精确地通过增加旋转坐标系的离心力来补偿。在这五点上的第三体(低重量)的力的净力为零,允许所述第三主体是完全静止的相对于该两个质量块。这就是为什么如果你把第三体在这些点中的一个,它会保持完全不动的旋转框架。

图像示出了具有第一质量,第二质量和旋转坐标系统相关联的区域。如果你把它们放在一起,这些区域形成的演技领域。这五个拉格朗日点用灰色区域表示。
前三拉格朗日点(表示为L1,L2和L3)被布置在一行中有两个大的机构和处于亚稳状态。 L4和L5被设置在在前面所述第二主体上的轨道和后部60°的角度,并处于稳定状态»。
通过factroom.ru