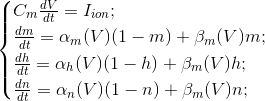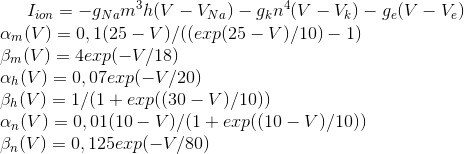The logic of thinking. Part 5. Brain Waves

So we come to the description of one of the key principles of the described model. This principle has not been used in any neural networks or in the description of the brain. In this regard, I am very encouraged to read the previous parts . As a minimum you must read fourth part without described below, will be completely incomprehensible.

In the previous article we talked about the fact that the activity of neurons is divided into induced and background. Echoes of the background activity observed, removing electroencephalogram. The recorded signals have a complicated shape, depending on the place of application of electrodes to the head, but, nevertheless, they quite clearly observed individual harmonic components.

Basic rhythms were named:

• alpha rhythm (8 to 13 Hz);
• beta rhythm (15 to 35 Hz);
• gamma rhythm (35 to 100 Hz);
• delta rhythm (from 0, 5 to 4 Hz);
• theta rhythm (5 to 7 Hz);
• sigma rhythm "spindles" (13 to 14 Hz).
  
  
  
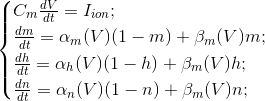
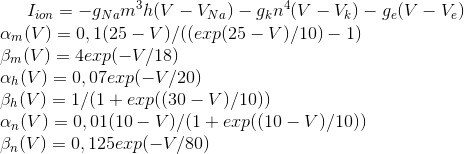
  These equations define the auto-wave process, ie prescribe neuron generate pulses. Hodgkin-Huxley model for complex modeling. Therefore, there is a lot to simplify it, to preserve the essential properties of the generation. The most popular models: Fitzhugh-Nagumo (Fitzhugh, 1961), Morris-Lecar (Morris C., Lecar H., 1981), Hindmarsh-Rose (Hindmarsh JL, and Rose RM, 1984). Many models, such as Hindmarsh-Rose can simulate both bursting activity and isolated spikes (see Figure below).
  
  
  
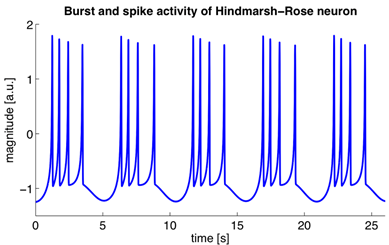
  bursting activity and spikes arising in the modeling of neural Hindmarsh-Rose i>
  
  Combining neurons that generate their own impulses in design, resembling the structure of the real cortex, unable to play a variety of effects that are typical for the group activity of real neurons. For example, it is possible to achieve global synchronization of neuronal activity or to cause the appearance of waves. The most well-known models: Wilson-Cowan (HR Wilson and JD Cowan, 1972) and Kuromoto (Kuramoto, 1984).
  
  EEG records the echoes of the joint activity of neurons, but it is clear that this activity has a specific spatio-temporal organization. Methods of optical observations of cortical activity allow us to see it live. In experimental animals bare patch of bark and inject a special dye that is sensitive to changes in electrical potential. Under the influence of the total oscillation of the membrane potential of neurons such dye changes its spectral properties. Although these changes are very small, they nevertheless may be fixed, for example with a diode array, which serves as a high-speed video camera. Optical methods do not allow us to look deeper into the bark and track the activity of individual neurons, but they allow a general idea of ​​the flow of wave processes on its surface.
  
  
  
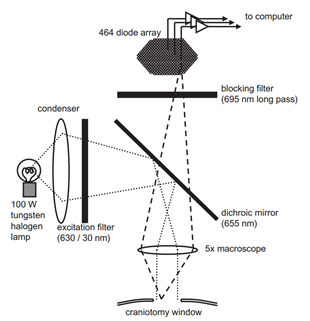
  The scheme of optical fixation activity of the cortex (Michael T. Lippert, Kentaroh Takagaki, Weifeng Xu, Xiaoying Huang, Jian-Young Wu, 2007) i>
  
  It was found that the rhythms of the brain correspond to waves arising in point sources and is distributed under the bark, like rings in the water. However, the wave front on the water diverges strongly in a circle, and the wave front of neuronal activity of the brain can be spread more complicated. The figure below shows the pattern of wave propagation at 5 millimeter part of the cortex of the rat brain.
  
  
  
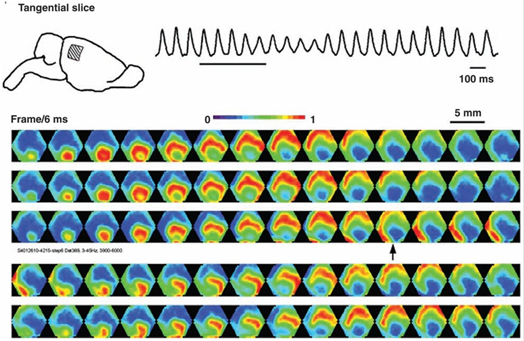
  The picture of the wave activity in the area of ​​the cerebral cortex of the rat. Potential shows a gradient from blue to red. 14 frames at intervals of 6 milliseconds cover one cycle of the wave (84 milliseconds - 12 Hz) (Michael T. Lippert, Kentaroh Takagaki, Weifeng Xu, Xiaoying Huang, Jian-Young Wu, 2007) i>
  
  Very interesting video and demonstration of wave activity are given in (W.-F. Xu, X.-Y. Huang, K. Takagaki, and J.-Y. Wu, 2007). There it is shown that waves can be sealed, before reaching the border zone of the cortex, may be reflected from the other zones and create counterpropagating waves can propagate double helices and create eddies.
  
  
  
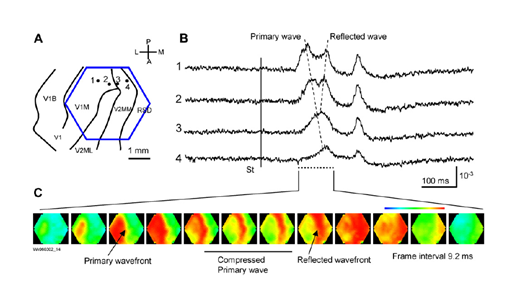
  Compression and reflection of waves in the primary visual cortex (W.-F. Xu, X.-Y. Huang, K. Takagaki, and J.-Y. Wu, 2007) i>
  
  Below is a video of the same work (W.-F. Xu, X.-Y. Huang, K. Takagaki, and J.-Y. Wu, 2007):
  
  
  
  Using the model of oscillating neurons can be in computer experiments to obtain similar wave pattern. But by itself this ripple is much sense. It is reasonable to assume that the wave activity - a mechanism of transfer and processing of information. But attempts to traditional models to explain the nature of this mechanism have not given tangible results. It seems logical to assume that the information is coded frequency and phase characteristics of neural signals. But this leads to the need to take into account the interference processes and raises more questions than it clarifies.
  
  There is a hypothesis that the wave of "scan" the crust by reading the information from it for its subsequent transfer (Pitts W., McCulloch WS, 1947). It looks quite sensibly, at least with respect to alpha waves and the primary visual cortex. The authors of this hypothesis, McCulloch and Pitts emphasized that the scan helps to explain an important phenomenon. The fact that the information from the primary visual cortex is projected further along the fibers through the bundles of white matter axons clearly insufficient in volume for the simultaneous transmission of all states of the cortex. So, they have concluded, scanning allows not only spatial but also temporal code that provides a consistent transmission of required information.
  
  This problem is the narrowness of projecting beams exists not only for the primary visual cortex, but also for all other areas of the brain. The number of fibers in the projection paths is much smaller than the number of neurons that form the spatial pattern of activity. Communication between zones is clearly not in a position parallel to convey the spatial distribution of the signal and, therefore, requires an understanding of how the compression and decompression of information broadcast by them. The assumption of the scan, although not answer the question about the mechanism of coding, nevertheless allows to set a correct questions.
  
  Our model in explaining the rhythms of the brain based on the above description of the nature of metabotropic activity. Using the idea that in the process of creating rhythms involved not only the synapses of neurons, but also metabotropic receptive clusters allows to obtain results that are qualitatively different from all the classical theories. But before going on to describe it, I want to make a warning. I will describe deliberately simplified idealized models, placing them into conformity certain processes inherent in the real brain, but not arguing that the brain works that way. Our task - to show the basic principles, understanding that evolution has progressed and their genuine implementation much trickier. You can draw an analogy with the development of computer technology. The modern computer is rather complicated, and if we begin to describe the basic principles of classical computing devices, it appears that in their pure form, is almost impossible to find in modern systems. The basic idea - the processor reads from program memory and data, performs actions on the data prescribed by the program and writes the results back to memory. Now add to this the use of various levels of cache, multithreading, hyperthreading, parallel computing using local, group and shared memory, and the like. And it turns out that it is difficult to find a real computer literal observance of simple rules. Actually, all this must be taken into account by matching the following description of the real work of the brain.
  
  So, we take the model portion of the cortex, which will create a compact pattern evoked activity. While the remaining question is how did this pattern. Simply, we assume that there are elements on which there is a constant pulse signal. In the figure below the neurons that form a pattern, marked in red. In reality, this corresponds to the cortex axons transmitting bursting activity, ie, issuing a series of spikes with high frequency. These axons may belong to the same neurons in cortex in a state of excitation caused by, or they can be fibers projection extending from the other parts of the brain.
  
  
  
  Pattern evoked activity i>
  
  Now make the free neurons generate rare random impulses. In this case we impose the condition that, for a random spike requires a certain level of environmental activity. This means that the random spikes can occur only in the vicinity of already active neurons. In our case, they appear in the vicinity of the pattern evoked activity. The figure below shows the occasional spikes in green.
  
  Normally all the activity of neurons that is not induced is called spontaneous or background. This is not very good, as adjusts the perception of all this activity as accidental. Next we show that, in general, the background activity is strictly predetermined and not at random. And only a small part of it - it really is a completely random spikes. Such random spikes and now we have created around the active pattern.
  
  
  
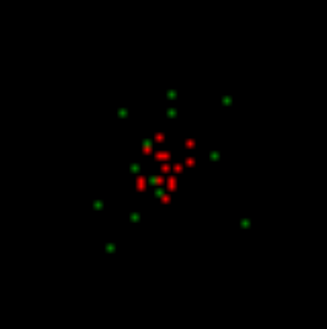
  The first step of the simulation. Spontaneous activity on the background caused by the activity of i>
  
  Simulate our formal neuron clusters metabotropic receptive. For this we give an opportunity to remember the neurons when necessary, painting activity entourage. And do not limit ourselves to one picture for one neuron, as it would be, to remember we are on the synapses, and allow each neuron to store a plurality of such paintings.
  
  Make it so that the presence of its own random spike and high ambient activity each time will remember the picture surrounding the base pulses (figure below). Further our neurons will produce individual spikes whenever be repeated one of the stored local patterns. In order not to confuse them with random spikes, we call these wave soldering.
  
  
  
  fixation area of ​​activity for one of the neurons that issued the spontaneous spike (he is in the center of the square). In the simulation, for simplicity, use square receptive fields, which although does not match the fields in pursuit of real neurons, not qualitatively affect the result i>
  
  As a result, the next step of the simulation (see Figure below), we get the picture, which will be the same as before, with neurons induced activity (red), neurons responded to the previous step stored locally the image (white), and the neurons generated spontaneous spike (green).
  
  
  
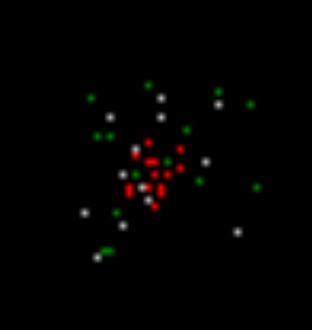
  The second step of the simulation. Red - active, white - wave activity, green - spontaneous activity i>
  
  Repeating the steps of the simulation, we obtain propagating over the cortex activity with a certain unique randomly generated pattern.
  Now we introduce the condition of fatigue neurons. Make it so that after a few metabotropic (wave) spikes neurons will lose the time required for relaxation, the ability to generate new impulses. This will lead to the fact that the activity will not propagate a continuous area, and pulsating waves, diverging from its source.
  
  To prevent "clogging" block the spontaneous activity in areas where large number of relaxing neurons. As a result, we obtain a ring of neurons with wave activity diverge from the pattern evoked activity (see Figure below).
  
  
  
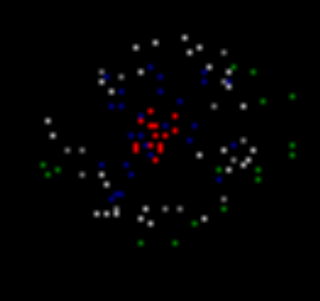
  The spread of the wave front. Blue - the neurons are in a state of relaxation i>
  
  The resulting wave is the distance from its center will lose density fronts and eventually dies out. In the figure below you can trace the first cycle of its life.
  
  
  
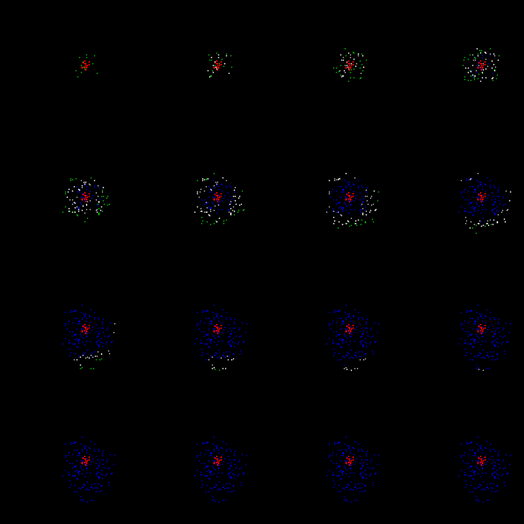
  The first cycle of the wave identifier i>
  
  After a period of relaxation will take place, will start a new wave. Now it will be picked up by neurons, already trained, and spread a little further. With each cycle of the wave will push the boundaries of its distribution until it reaches the edges of the zone. To prevent unlimited growth of the density of the wave front, we introduce another constraint: the prohibition of spontaneous activity of the neurons when the total activity around them exceeds a certain threshold.
  
  After some time we will get the bark, training impart unique in its pattern of wave activity, corresponding to a predetermined pattern initially evoked activity (see Figure below).
  
  
  
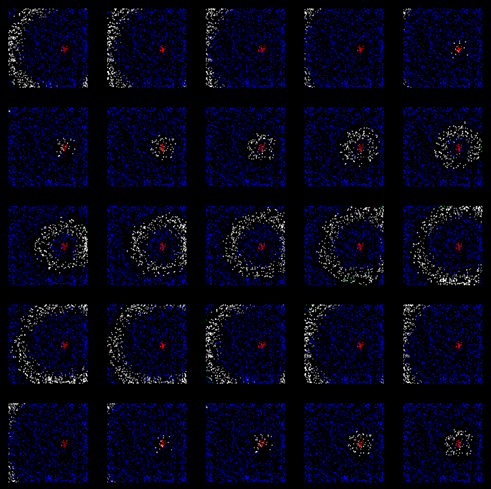
  The spread of wave already trained crust (after 200 cycles of training) i>
  
  Below is a video of the wave process of learning:
  
  
  
  Note: When the bark is already trained on the wave propagation from a specific pattern, spontaneous (random) spikes disappear. This "pilot" wave formed by the wave, non-random spikes. Random spikes appear only in the training, when the wave front reaches even untrained or poorly trained territories. At this point, spontaneous impulses creates random wave continuation pattern that immediately stored on the surface of neurons involved in this wave. But once the training is over, the wave pattern from the familiar crust begins to spread already creates a wave pattern, each cycle exactly repeating in its path is the same already nonrandom pattern.
  
  Education crust does not necessarily have to be gradual. In modeling the choice of parameters can ensure that originated wave was self-sufficient. That is to say that it is not attenuated in the first cycle, and immediately spread to the entire space (see Figure below).
  
  
  
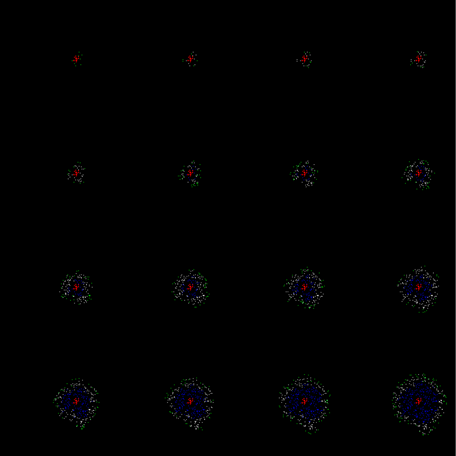
  Example persistent on the first cycle of the wave propagation learning i>
  
  Since the width of wave front is constant, the surface area increases with distance from the source. This corresponds to what is actively involved in the dissemination of more neurons. If we trace the total potential created by them, then we obtain the graphs, similar to what we see on entsifologrammah (shown below).
  
  
  
  Graph rhythmic activity patterns with a single source i>
  
  Please note that the appearance of rhythms observed in these "electroencephalograms," - this is not the rhythm of "breathing" of the cortex. That is not synchronized bursts of joint activity, as expected in most existing models, and the change in the number of neurons involved in the propagation of the outgoing waves. If new waves are emitted even before the preceding wave fronts disappear, their addition will give a smoother picture. At a certain choice of parameters on the model reproduces a situation where the wave propagation is accompanied by almost total rhythmic activity. This can be correlated with the fact that about 10 percent of the people on the electroencephalogram wave activity can not be traced.
  
  If we now take a new pattern evoked activity, the crust will create waves propagating from him. Moreover, this bark is trained to create waves for any sustainable pattern evoked activity. Due to the fact that the same neuron can store a plurality of local images, it can be directly part of the plurality of different waves corresponding to different patterns. If we want more unique waves, enough with the accumulation of neuron stored it reduces the local likelihood of spontaneous spike.
  
  For local images stored makes sense to introduce the mechanism of consolidation. That is not to capture the image directly on the century, and set the time during which the image should be repeated a number of times. Since learning the wave propagation and formation of stable patterns evoked activity - parallel processes, the consolidation can afford to erase the traces of educational failure.
  
  But the most important thing in all of this - is the uniqueness of each of the resulting wave of stories. In any place, through which the wave, it creates a unique, characteristic only for her figure. This means that if there is a pattern of cortical surface evoked activity, which encodes an event, the wave caused by them by spreading information about it over the entire space of the cortex. In each place, this wave will create a unique pattern that is unique only for this event. Any other event creates in this point a pattern associated with its wave.
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  
  References
  
  If somewhere too brief, unclear or unintelligible stated, please unsubscribe in the comments.
  
  Previous parts:
  Part 1. Neuron
  Part 2. Factors
  Part 3: Perceptron, convolutional network
  Part 4. Background activity
  
  Alexei Redozubov (2014)