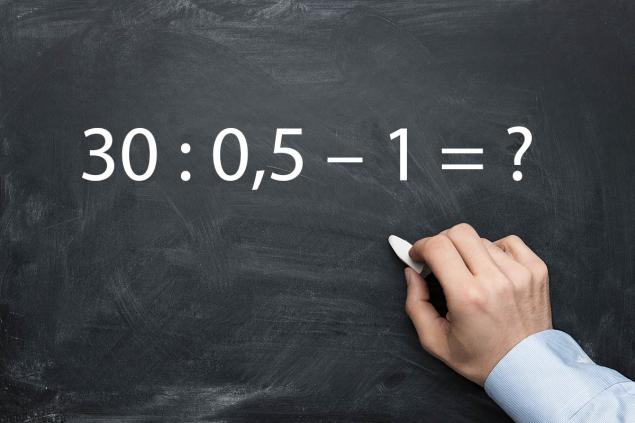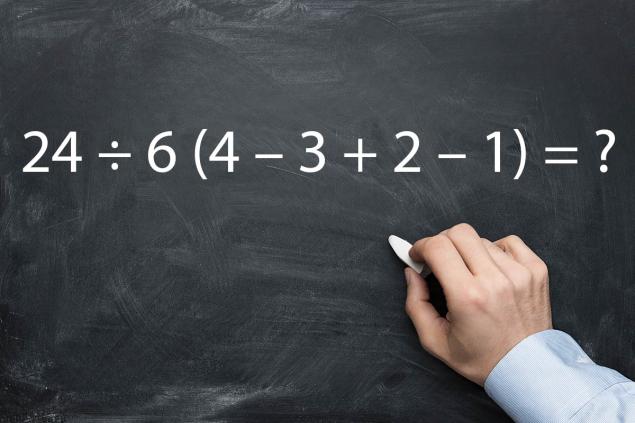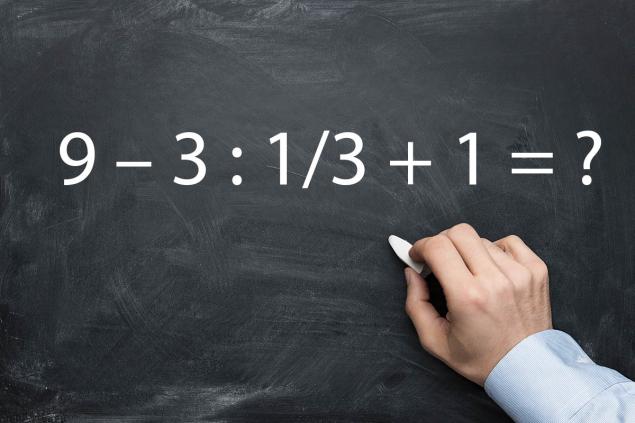216
0.1
2022-11-22
Советский двоечник решил пример за минуту, проверь, осилишь ли ты его
Какими бы уверенными в себе ни были взрослые люди, решение простых примеров далеко не всегда дается им легко. Однако не спеши стыдиться этого! Время идет, и даже базовые школьные знания забываются. Это нормально, ведь большей частью из них мы попросту не пользуемся.
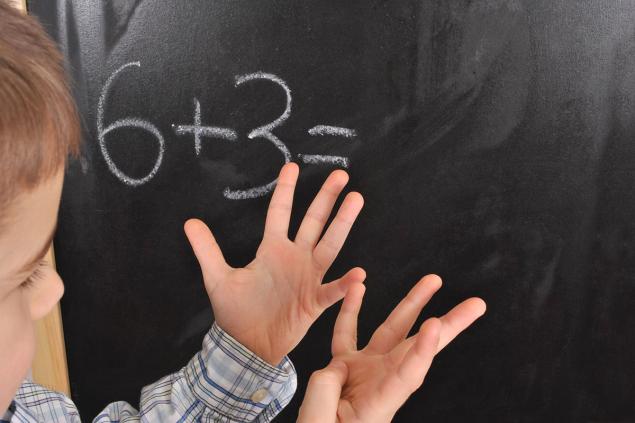
Давай договоримся так. Сегодня ты попробуешь обуздать парочку школьных примеров с заковыркой. Если не все из них тебе удастся решить правильно, ты не станешь расстраиваться. Пускай это будет небольшой встряской для ума. Попробуй отвлечься от тревог и бытовых дел. Сейчас это особенно ценно!
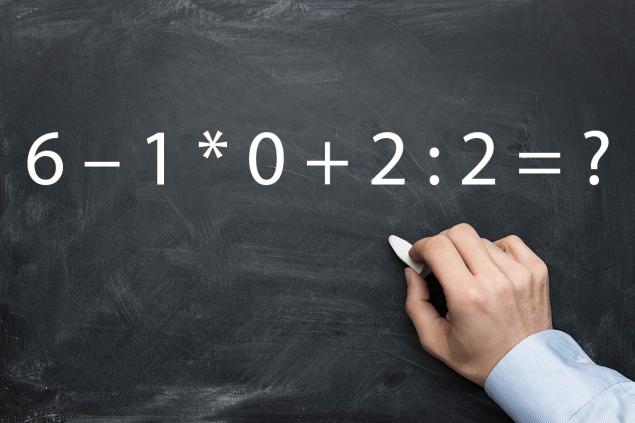
Для пущего эффекта можешь засечь, за какое количество времени тебе удастся решить этот простейший пример. Второклассники, к примеру, решают еще за пару секунд. Ладно-ладно, двоечникам может понадобиться около минуты. А тебе?

А теперь давай разбираться. В таких примерах очень важно помнить о порядке выполнения арифметических действий. Сначала мы смотрим на то, есть ли в примере умножение или деление. Как видишь, такие действия есть. Выходит, что 1 × 0 = 0. А 2 ÷ 2 = 1.
Возвращаемся к основной части примера и выполняем действия по очереди. Таким образом, сначала мы отнимаем от шести ноль, а затем к полученной шестерке прибавляем единицу: 6 – 0 + 1 = 7. Вот и все премудрости!

Кстати, если бы в этом примере были скобочки, сперва мы бы решили то, что находится внутри них. Но их не было, потому мы перешли к вычислениям второй ступени, то есть делению и умножению. Как видишь, на самом деле в этом примере нет ничего сложного. Теперь ты без труда решишь любую задачку такой же сложности. Ура!
С примерами на сегодня покончено! Надеюсь, тебе удалось разбавить атмосферу рутинной повседневности и вспомнить школьные времена. Расскажи, сколько примеров тебе удалось решить правильно? Жду тебя в комментариях!
Давай договоримся так. Сегодня ты попробуешь обуздать парочку школьных примеров с заковыркой. Если не все из них тебе удастся решить правильно, ты не станешь расстраиваться. Пускай это будет небольшой встряской для ума. Попробуй отвлечься от тревог и бытовых дел. Сейчас это особенно ценно!
Решение простых примеров
Итак, первый математический пример прямо перед тобой. Внимательно изучи его и не спеши делать выводы. Вспомни, какова последовательность действий в подобных примерах. Будем считать, что это была маленькая подсказка от нашей редакции.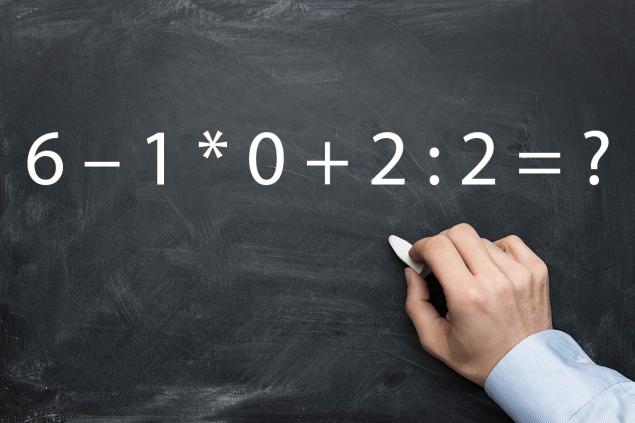
Для пущего эффекта можешь засечь, за какое количество времени тебе удастся решить этот простейший пример. Второклассники, к примеру, решают еще за пару секунд. Ладно-ладно, двоечникам может понадобиться около минуты. А тебе?

А теперь давай разбираться. В таких примерах очень важно помнить о порядке выполнения арифметических действий. Сначала мы смотрим на то, есть ли в примере умножение или деление. Как видишь, такие действия есть. Выходит, что 1 × 0 = 0. А 2 ÷ 2 = 1.
Возвращаемся к основной части примера и выполняем действия по очереди. Таким образом, сначала мы отнимаем от шести ноль, а затем к полученной шестерке прибавляем единицу: 6 – 0 + 1 = 7. Вот и все премудрости!

Кстати, если бы в этом примере были скобочки, сперва мы бы решили то, что находится внутри них. Но их не было, потому мы перешли к вычислениям второй ступени, то есть делению и умножению. Как видишь, на самом деле в этом примере нет ничего сложного. Теперь ты без труда решишь любую задачку такой же сложности. Ура!
Подборка примеров с заковыркой
- В этом примере тебя может смутить дробное число 0,5. И это неудивительно, что рука сразу же хочет потянуться за калькулятором. Как же делить на такую натуральную дробь? Верю, что у тебя получится. А если нет, то листай статью вниз: там ты найдешь ответ.
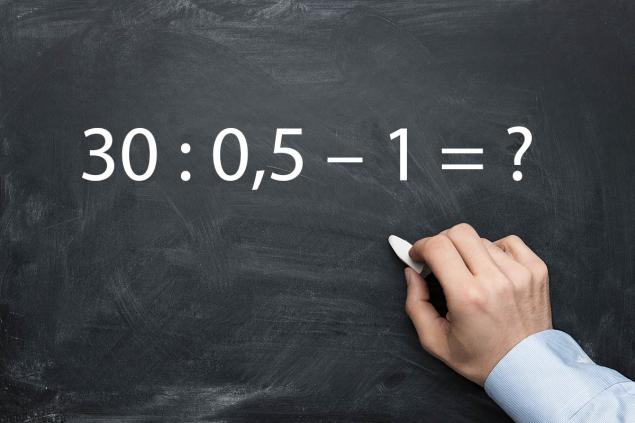
- Тут всё просто. Вспомни о том, что мы обсуждали в самом начале статьи. Порядок выполнения арифметических действий поможет тебе во всём разобраться. Дерзай!
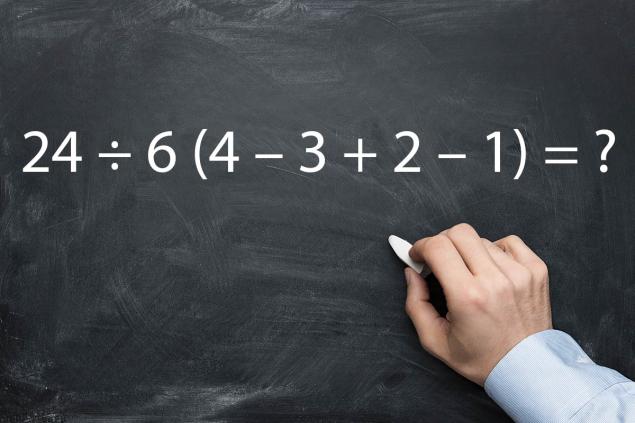
- В этом примере тебе нужно поделить число на дробь. Интересно, а ты помнишь, как это делается?
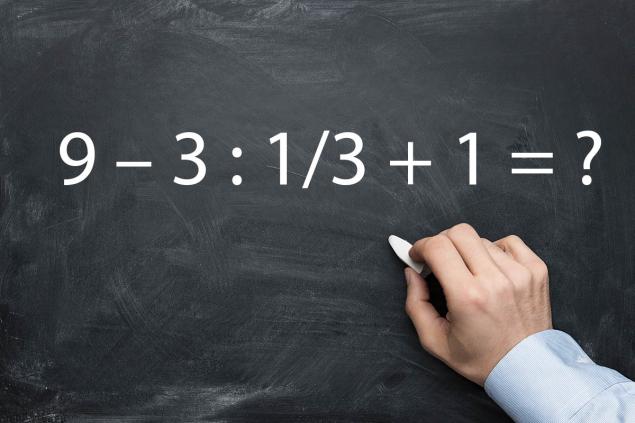
Ответы
- Тот, кто часто сталкивается с математикой в жизни, хорошо знает, что делить на 0,5 — это всё равно что умножить на 2. А потому мы получаем вполне простой и понятный пример, который не составит труда решить.
А именно: 30 × 2 – 1 = 60 – 1 = 59. - Разбираемся со скобками, а затем по очереди решаем каждое действие. В результате получаем: 24 ÷ 6 (4 – 3 + 2 – 1) = 24 ÷ 6 × 2 = 4 × 2 = 8.
- Для решения этого примера нужно вспомнить еще одну простую фишку из школьной программы по математике. Поделить число на дробь — это то же самое, что умножить ее на эту же дробь, предварительно поменяв числитель и знаменатель местами. Тогда наш пример получает немного другой, но более понятный вид: 9 – 3 * 3 + 1 = 9 – 9 + 1 = 1.
С примерами на сегодня покончено! Надеюсь, тебе удалось разбавить атмосферу рутинной повседневности и вспомнить школьные времена. Расскажи, сколько примеров тебе удалось решить правильно? Жду тебя в комментариях!
Портал БАШНЯ. Копирование, Перепечатка возможна при указании активной ссылки на данную страницу.
Почему я больше не варю крупы, а просто заливаю водой, феноменальный способ
Oosto керуватиме River Spirit за допомогою розпізнавання облич