1466
Ентропія? Це легко!
Цей пост є безкоштовним перекладом відповіді Марка Ейченлауба на запитання Який інтуїтивно зрозумілий спосіб зрозуміти ентропію?
Ентропія. Можливо, це один з найскладніших концепцій, щоб зрозуміти, що ви можете відвідати курс фізики, принаймні, коли мова йде про класичну фізику. Випускники фізики можуть пояснити, що це таке. Більшість проблем з розумінням ентропії, однак, можна вирішити розумінням одне. Ентропія якісно відрізняється від інших термодинамічних кількостей, таких як тиск, об'єм або внутрішня енергія, адже це не властивість системи, але з того, як ми переглядаємо її. На жаль, в ході термодинаміки зазвичай розглядається разом з іншими термодинамічними функціями, що посилює непорозуміння.
 р.
р.
Що таке ентропія?
У лавці,
Наприклад, якщо ви попросите мене, де я живу, і я відповідь: в Росії мій антропія для вас буде високою, після усього, Росія велика країна. Якщо я даю вам мій поштовий код, 603081, мій антропій зменшиться для вас, як ви отримаєте більше інформації.
Поштовий індекс має шість цифр, тому я дав вам шість символів інформації. Ентропія ваших знань мене впав близько 6 символів. (Не дійсно, тому що деякі індекси відповідають більшій кількості адрес, але ми нехтуємо цим.)

Або розглянемо ще один приклад. Покажіть, що їх сума 30. Знаючи лише те, що ви не можете розповісти про те, які конкретні числа на кожній з кісток – вам не вистачає інформації. Ці риси на кістках статистичної фізики називають мікродержавами, а загальна сума (30 у нашому випадку) називається макростатами. Є 2,930,455 мікродержави, які відповідають сумі 30. Отже, ентропія цієї макростати становить приблизно 6.5 символів (халф обумовлено тим, що коли ви номеруєте мікродержави для того, щоб в сімму біті не всі цифри доступні для вас, але тільки 0, 1 і 2).
Що, якщо я сказав, що це було 59? Є тільки 10 можливих мікродержав для цієї макростати, тому його ентропія є тільки одним характером. Як видно, різні макростати мають різні ентропії.
Покажіть, що сума перших п'яти кісток становить 13 і сума іншої п'ятірки 17, так що загальна знову 30. Ви, однак, мають більш детальну інформацію в цьому випадку, тому ентропія системи для вас повинна вийти. І, дійсно, 13 на п'ять кісток можна отримати 420 різними способами, і 17 - 780, тобто загальна кількість мікродержавів становить лише 420 x 780 = 327 600. Ентропія такої системи становить приблизно один характер менше, ніж у першому прикладі.
Виміряємо ентропію як кількість символів, необхідних для запису кількості мікродержав. Математично, цей номер визначається як логарифм, тому шляхом денотування ентропії з символом S, а кількість мікродержав з символом Ω ми можемо писати:
S = Лог Ω
Це нічого більше, ніж формула Boltzmann (з точністю фактора к, що залежить від одиниць вимірювання, обраних) для ентропії. Якщо один мікростат відповідає макростату, його ентропія за цією формулою є нуль. Якщо у вас є дві системи, то загальна ентропія дорівнює сумі ентропій кожного з цих систем, так як журнал(AB) = log A + log Б.

З наведеного опису стає зрозуміло, чому не варто думати про ентропію як властивість системи. Система має певну внутрішню енергію, імпульс, заряд, але не має певного ентропію: ентропія десять кісток залежить від того, чи знаєте ви тільки їх загальну суму, а також часткові суми п'яти кісток.
Іншими словами, ентропія як ми описуємо систему. І це дуже відрізняється від інших кількостей, які ми працюємо з фізики.
Фізичний приклад: газ під поршневий
Класична система, яка вважається фізикою, є газом в посудині під поршнем. Мікростата газу - позиція і імпульс (опадність) кожної молекули. Це еквівалентно дізнатися значення на кожній кістці на прикладі раніше. макростата газу описується такою кількістю як тиск, щільність, об'єм, хімічна композиція. Це як сума значень на кістках.
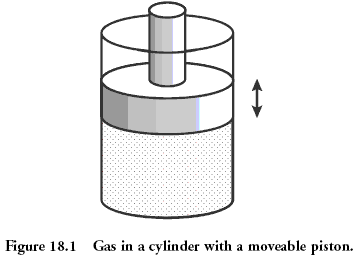
Кількість, яка описує макростату, може бути пов'язана між собою за допомогою так званого «державного рівняння». Це наявність цього з'єднання, що дозволяє нам, не знаючи мікростатів, щоб прогнозувати те, що буде відбуватися в нашій системі, якщо ми починаємо нагрівати його або переміщати поршня. Для ідеального газу рівняння держави простий:
р = ρ
Хоча ви, ймовірно, більш знайомі з рівняння Клапєрон-Менделеєва, pV = νRT є однаковим рівнянням, тільки додаючи пару констанцій, щоб заплутати вас. Більшість мікродержав, які відповідають даній макростаті, тобто більші частинки, які роблять нашу систему, краще рівняння держави описує її. Для газу характерні значення кількості частинок рівні Авогадро, тобто близько 1023.
Ускладнення типу тиску, температури і щільності називаються середнім, так як вони є середнім проявом постійно мінливих мікродержав, що відповідають даній макростаті (або замість цього макростати близько до нього). Для того, щоб дізнатися, які мікростати в системі, нам потрібно багато інформації — нам потрібно знати позицію і швидкість кожної частинки. Кількість даної інформації називається ентропією.
Як змінюється ентропія з макродержавою? Легко зрозуміти. Наприклад, якщо ми нагріваємо газ трохи, швидкість його частин збільшиться, тому ступінь нашого ігнорування про цю швидкість збільшиться, тобто ентропія збільшиться. Або, якщо ми збільшуємо обсяг газу, витягаючи поршня, ступінь нашого ігнорування положення частинок збільшується, а також підвищується ентропія.
Тверді тіла та потенційна енергія
Якщо розглядати замість газу тверде тіло, особливо одне з замовленою структурою, як у кристалах, наприклад, шматком металу, його ентропія буде невеликою. Чому? Знаючи позицію одного атома в такій структурі, ви знаєте позицію всіх інших (вони розташовуються в регулярній кристалічній структурі), околиць атомів невеликі, оскільки вони не можуть літати далеко від їх положення і тільки злегка коливання навколо позиції рівноваги.
3286954
Якщо шматок металу знаходиться в гравітаційному полі (наприклад, піднімається над поверхнею Землі), то потенційна енергія кожного атома в металі приблизно дорівнює потенційній енергії інших атомів, а ентропія, пов'язана з цією енергією низька. Це відрізняє потенційну енергію від кінетичної енергії, яка для теплового руху може істотно відрізнятися від атома до атому.
Якщо виділяється шматок металу до певної висоти, її потенційна енергія буде перетворена в кінетичну енергію, але ентропія навряд чи збільшиться, оскільки всі атоми будуть рухатися приблизно таким же чином. Але коли шматочок потрапляє до землі, під час впливу металеві атоми отримають випадковий напрямок руху, а ентропія різко збільшиться. Кінетична енергія спрямованого руху буде перетворена в кінетичну енергію теплового руху. До удару ми знаємо грубо, як кожен атом переїхав, і зараз ми втратили цю інформацію.
Витримує другий закон термодинаміки
Другий закон термодинамічних станів, які завжди посилюються. Ми можемо зараз зрозуміти, чому: тому, що не можна раптом отримати більше інформації про мікродержави. Після того, як ви втратили інформацію про мікродержаву (наприклад, коли шматок металевих зображень в грунті), ви не можете отримати його назад.

Повернемося до дайвінгу. Пам'ятайте, що макростата 59-літа має дуже низьку ентропію, але це не легко отримати його. Якщо ви перекидаємо кальцинацію і знову, то будуть реалізовані суми (макростати), які відповідають більшій кількості мікродержав, тобто макростати з високою ентропією. Найбільша ентропія має суму від 35, і вона випадає частіше, ніж інші. Це те, що другий закон про термодинаміку говорить. Будь-яка випадкова (неконтрольована) взаємодія призводить до збільшення ентропії, принаймні до досягнення максимального.
Змішування газу
І ще один приклад для армування. У нас є контейнер, що містить два гази, відокремлені розділом, розташованим в середині контейнера. Давайте подзвонимо молекули одного газу синього і іншого червоного.
Якщо ви відкриєте розділ, гази почнуть змішати, тому що кількість мікродержав, в яких гази змішуються набагато більше, ніж мікродержави, в яких вони відокремлені, і всі мікродержави, природно, однаково ймовірні. Коли ми відкрили septum, для кожної молекули, ми втратили інформацію про яку сторону septum. Якщо молекули були N, то N біти інформації були втрачені (біти та символи, в цьому контексті фактично однакові, і відрізняються лише певним постійним множником).
Зцілення з демоном Maxwell
Нарешті, ми розглянемо рішення про знаменитий парадокс Максвелл в рамках нашої парадигми. Нагадуємо, що це так: Насадки ми змішували гази синіх і червоних молекул. Ми покладемо розділ, зробивши невелику дірку в ній, в яку одягаємо явний демон. Його завдання - передати зліва направо тільки червоний, а з правого наліво тільки синій. Очевидно, що після того, як гази будуть відокремлюватися знову: всі сині молекули будуть до лівої з перегородки, і всі червоні – вправо.
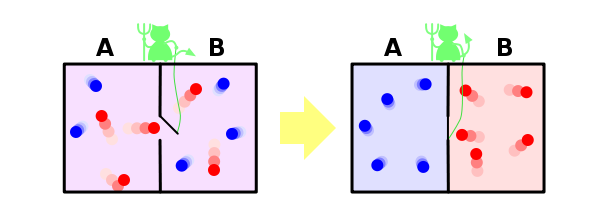
Виявляється, що наша демон опускає антропію системи. Ніщо не сталося з демоном, тобто його антропія не змінилася, а наша система була закрита. Виявляється, що ми знайшли приклад, коли другий закон термодинаміки не тримається! Як це можливо?
Вирішуючи цей парадокс, проте, дуже простий. Ентропія не є власністю системи, але наших знань цієї системи. Ми не знаємо багато про систему, тому ми думаємо, що її ентропія зменшується. Але наш демон знає багато про систему – до відокремлених молекул, він повинен знати позицію і швидкість кожного з них (принаймні, як він підходи до неї). Якщо знає все про молекули, то з точки зору, ентропія системи фактично нуль - він просто не має ніяких відомостей про неї. У цьому випадку антропія системи була нульовою і залишалася нульовою, а другий закон термодинаміки не порушував в будь-яку точку.
Але навіть якщо демон не знає всю інформацію про мікродержаву системи, він не повинен знати колір молекули, що наближається до нього, щоб дізнатися, чи не пропустити його. І якщо загальна кількість молекул Н, то демон повинен мати N біти інформації про систему - але це скільки інформації, яку ми втратили при відкритті розділу. Таким чином, кількість інформації, що втратила, є такою ж, як і кількість інформації, яку потрібно отримати про систему для того, щоб повернутися до свого первісного стану, і це звучить логічно, і знову не суперечить другому закону термодинаміки.
Джерело: geektimes.ru/post/246406/
Ентропія. Можливо, це один з найскладніших концепцій, щоб зрозуміти, що ви можете відвідати курс фізики, принаймні, коли мова йде про класичну фізику. Випускники фізики можуть пояснити, що це таке. Більшість проблем з розумінням ентропії, однак, можна вирішити розумінням одне. Ентропія якісно відрізняється від інших термодинамічних кількостей, таких як тиск, об'єм або внутрішня енергія, адже це не властивість системи, але з того, як ми переглядаємо її. На жаль, в ході термодинаміки зазвичай розглядається разом з іншими термодинамічними функціями, що посилює непорозуміння.
 р.
р.Що таке ентропія?
У лавці,
Наприклад, якщо ви попросите мене, де я живу, і я відповідь: в Росії мій антропія для вас буде високою, після усього, Росія велика країна. Якщо я даю вам мій поштовий код, 603081, мій антропій зменшиться для вас, як ви отримаєте більше інформації.

Поштовий індекс має шість цифр, тому я дав вам шість символів інформації. Ентропія ваших знань мене впав близько 6 символів. (Не дійсно, тому що деякі індекси відповідають більшій кількості адрес, але ми нехтуємо цим.)

Або розглянемо ще один приклад. Покажіть, що їх сума 30. Знаючи лише те, що ви не можете розповісти про те, які конкретні числа на кожній з кісток – вам не вистачає інформації. Ці риси на кістках статистичної фізики називають мікродержавами, а загальна сума (30 у нашому випадку) називається макростатами. Є 2,930,455 мікродержави, які відповідають сумі 30. Отже, ентропія цієї макростати становить приблизно 6.5 символів (халф обумовлено тим, що коли ви номеруєте мікродержави для того, щоб в сімму біті не всі цифри доступні для вас, але тільки 0, 1 і 2).
Що, якщо я сказав, що це було 59? Є тільки 10 можливих мікродержав для цієї макростати, тому його ентропія є тільки одним характером. Як видно, різні макростати мають різні ентропії.
Покажіть, що сума перших п'яти кісток становить 13 і сума іншої п'ятірки 17, так що загальна знову 30. Ви, однак, мають більш детальну інформацію в цьому випадку, тому ентропія системи для вас повинна вийти. І, дійсно, 13 на п'ять кісток можна отримати 420 різними способами, і 17 - 780, тобто загальна кількість мікродержавів становить лише 420 x 780 = 327 600. Ентропія такої системи становить приблизно один характер менше, ніж у першому прикладі.
Виміряємо ентропію як кількість символів, необхідних для запису кількості мікродержав. Математично, цей номер визначається як логарифм, тому шляхом денотування ентропії з символом S, а кількість мікродержав з символом Ω ми можемо писати:
S = Лог Ω
Це нічого більше, ніж формула Boltzmann (з точністю фактора к, що залежить від одиниць вимірювання, обраних) для ентропії. Якщо один мікростат відповідає макростату, його ентропія за цією формулою є нуль. Якщо у вас є дві системи, то загальна ентропія дорівнює сумі ентропій кожного з цих систем, так як журнал(AB) = log A + log Б.

З наведеного опису стає зрозуміло, чому не варто думати про ентропію як властивість системи. Система має певну внутрішню енергію, імпульс, заряд, але не має певного ентропію: ентропія десять кісток залежить від того, чи знаєте ви тільки їх загальну суму, а також часткові суми п'яти кісток.
Іншими словами, ентропія як ми описуємо систему. І це дуже відрізняється від інших кількостей, які ми працюємо з фізики.
Фізичний приклад: газ під поршневий
Класична система, яка вважається фізикою, є газом в посудині під поршнем. Мікростата газу - позиція і імпульс (опадність) кожної молекули. Це еквівалентно дізнатися значення на кожній кістці на прикладі раніше. макростата газу описується такою кількістю як тиск, щільність, об'єм, хімічна композиція. Це як сума значень на кістках.

Кількість, яка описує макростату, може бути пов'язана між собою за допомогою так званого «державного рівняння». Це наявність цього з'єднання, що дозволяє нам, не знаючи мікростатів, щоб прогнозувати те, що буде відбуватися в нашій системі, якщо ми починаємо нагрівати його або переміщати поршня. Для ідеального газу рівняння держави простий:
р = ρ
Хоча ви, ймовірно, більш знайомі з рівняння Клапєрон-Менделеєва, pV = νRT є однаковим рівнянням, тільки додаючи пару констанцій, щоб заплутати вас. Більшість мікродержав, які відповідають даній макростаті, тобто більші частинки, які роблять нашу систему, краще рівняння держави описує її. Для газу характерні значення кількості частинок рівні Авогадро, тобто близько 1023.
Ускладнення типу тиску, температури і щільності називаються середнім, так як вони є середнім проявом постійно мінливих мікродержав, що відповідають даній макростаті (або замість цього макростати близько до нього). Для того, щоб дізнатися, які мікростати в системі, нам потрібно багато інформації — нам потрібно знати позицію і швидкість кожної частинки. Кількість даної інформації називається ентропією.
Як змінюється ентропія з макродержавою? Легко зрозуміти. Наприклад, якщо ми нагріваємо газ трохи, швидкість його частин збільшиться, тому ступінь нашого ігнорування про цю швидкість збільшиться, тобто ентропія збільшиться. Або, якщо ми збільшуємо обсяг газу, витягаючи поршня, ступінь нашого ігнорування положення частинок збільшується, а також підвищується ентропія.
Тверді тіла та потенційна енергія
Якщо розглядати замість газу тверде тіло, особливо одне з замовленою структурою, як у кристалах, наприклад, шматком металу, його ентропія буде невеликою. Чому? Знаючи позицію одного атома в такій структурі, ви знаєте позицію всіх інших (вони розташовуються в регулярній кристалічній структурі), околиць атомів невеликі, оскільки вони не можуть літати далеко від їх положення і тільки злегка коливання навколо позиції рівноваги.
3286954
Якщо шматок металу знаходиться в гравітаційному полі (наприклад, піднімається над поверхнею Землі), то потенційна енергія кожного атома в металі приблизно дорівнює потенційній енергії інших атомів, а ентропія, пов'язана з цією енергією низька. Це відрізняє потенційну енергію від кінетичної енергії, яка для теплового руху може істотно відрізнятися від атома до атому.
Якщо виділяється шматок металу до певної висоти, її потенційна енергія буде перетворена в кінетичну енергію, але ентропія навряд чи збільшиться, оскільки всі атоми будуть рухатися приблизно таким же чином. Але коли шматочок потрапляє до землі, під час впливу металеві атоми отримають випадковий напрямок руху, а ентропія різко збільшиться. Кінетична енергія спрямованого руху буде перетворена в кінетичну енергію теплового руху. До удару ми знаємо грубо, як кожен атом переїхав, і зараз ми втратили цю інформацію.
Витримує другий закон термодинаміки
Другий закон термодинамічних станів, які завжди посилюються. Ми можемо зараз зрозуміти, чому: тому, що не можна раптом отримати більше інформації про мікродержави. Після того, як ви втратили інформацію про мікродержаву (наприклад, коли шматок металевих зображень в грунті), ви не можете отримати його назад.

Повернемося до дайвінгу. Пам'ятайте, що макростата 59-літа має дуже низьку ентропію, але це не легко отримати його. Якщо ви перекидаємо кальцинацію і знову, то будуть реалізовані суми (макростати), які відповідають більшій кількості мікродержав, тобто макростати з високою ентропією. Найбільша ентропія має суму від 35, і вона випадає частіше, ніж інші. Це те, що другий закон про термодинаміку говорить. Будь-яка випадкова (неконтрольована) взаємодія призводить до збільшення ентропії, принаймні до досягнення максимального.
Змішування газу
І ще один приклад для армування. У нас є контейнер, що містить два гази, відокремлені розділом, розташованим в середині контейнера. Давайте подзвонимо молекули одного газу синього і іншого червоного.
Якщо ви відкриєте розділ, гази почнуть змішати, тому що кількість мікродержав, в яких гази змішуються набагато більше, ніж мікродержави, в яких вони відокремлені, і всі мікродержави, природно, однаково ймовірні. Коли ми відкрили septum, для кожної молекули, ми втратили інформацію про яку сторону septum. Якщо молекули були N, то N біти інформації були втрачені (біти та символи, в цьому контексті фактично однакові, і відрізняються лише певним постійним множником).
Зцілення з демоном Maxwell
Нарешті, ми розглянемо рішення про знаменитий парадокс Максвелл в рамках нашої парадигми. Нагадуємо, що це так: Насадки ми змішували гази синіх і червоних молекул. Ми покладемо розділ, зробивши невелику дірку в ній, в яку одягаємо явний демон. Його завдання - передати зліва направо тільки червоний, а з правого наліво тільки синій. Очевидно, що після того, як гази будуть відокремлюватися знову: всі сині молекули будуть до лівої з перегородки, і всі червоні – вправо.

Виявляється, що наша демон опускає антропію системи. Ніщо не сталося з демоном, тобто його антропія не змінилася, а наша система була закрита. Виявляється, що ми знайшли приклад, коли другий закон термодинаміки не тримається! Як це можливо?
Вирішуючи цей парадокс, проте, дуже простий. Ентропія не є власністю системи, але наших знань цієї системи. Ми не знаємо багато про систему, тому ми думаємо, що її ентропія зменшується. Але наш демон знає багато про систему – до відокремлених молекул, він повинен знати позицію і швидкість кожного з них (принаймні, як він підходи до неї). Якщо знає все про молекули, то з точки зору, ентропія системи фактично нуль - він просто не має ніяких відомостей про неї. У цьому випадку антропія системи була нульовою і залишалася нульовою, а другий закон термодинаміки не порушував в будь-яку точку.
Але навіть якщо демон не знає всю інформацію про мікродержаву системи, він не повинен знати колір молекули, що наближається до нього, щоб дізнатися, чи не пропустити його. І якщо загальна кількість молекул Н, то демон повинен мати N біти інформації про систему - але це скільки інформації, яку ми втратили при відкритті розділу. Таким чином, кількість інформації, що втратила, є такою ж, як і кількість інформації, яку потрібно отримати про систему для того, щоб повернутися до свого первісного стану, і це звучить логічно, і знову не суперечить другому закону термодинаміки.
Джерело: geektimes.ru/post/246406/
Підсумок з електричним скутером допоможе зловити площину
20 березня сонячна електрика відключить 35 ГВт електростанцій з європейської сітки